
5、作不同时刻的波形图问题
解此类问题,一般有“描点法”和“波形平移法”。
(1)描点法:如已知波的传播方向,我们可以根据上面介绍的方法判定各个质点的振动方向,再根据振动规律来确定每个质点经△t后的位置,最后用逐点描迹的方法画出波形图,此种方法一般取几个特殊点来分析其振动情况。
例2、一列简谐横波在X轴上传播,波速为20m/s,已知t=0时刻的波形图如图(2)中实线所示,图中N处的质点此时正经过平移位置沿y轴正方向运动。画出t=0.5秒后的波形图。
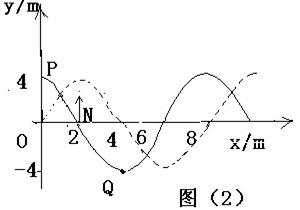
分析与解 T=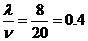 (s)
(s)
周期数
n= (个)
(个)
因t=0时,N点在平衡位置沿y轴正方向运动,取P、Q、N点为研究对象,则N质点经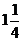 周期在波峰位置,P、Q点均在平衡位置,这样可以画出t=0.5秒时的波形图,如图(2)虚线所示。
周期在波峰位置,P、Q点均在平衡位置,这样可以画出t=0.5秒时的波形图,如图(2)虚线所示。
4、如何判断质点的振动方向与波的传播方向
(1)带动法:横波向前传播的过程中,只是振动的形式向前传播的过程。是前面的质点的振动带动后面的质点的振动(简称为“前”带“后”)。注意观察分析课本“绳波形成”的插图。
(2)微平移法:由于机械波在均匀介质中振动形式是匀速传播的,因此在原有的t时刻波形图上,沿着波的传播方向向右或向左(X轴的正方向或负方向)平推小于四分之一波长的波,下一时刻t+△t波将向这一方向传播或质点将向这方向振动。
(3)手推法:使(左手或右手)四指的方向指向波峰或波谷,手心的方向指向与质点振动的方向相同,手掌的方向就是波传播的方向。
(4)三角形法(如图)
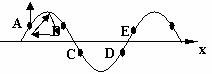
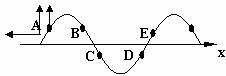
(5)逆向描点法:(逆向复描波形法)运用逆向复描波形法解答十分简捷。即,手握一支笔,逆着波的传播方向复描已知波形,凡复描时笔尖沿波形向上经过的质点,此刻均向上运动;凡复描时笔尖沿波形向下经过的质点,此刻均向下运动(波峰和波谷点除外)。如图所示。
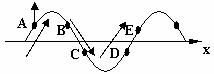
(6)头头(尾尾)相对法:如图所示,上面的箭头表示波传播的方向,左侧的箭头表示B、C两质点振动的方向。
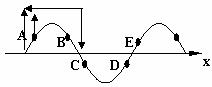
(7)同侧法:所谓同侧法既质点振动的方向与波传播的方向在波形图的同侧。如图所示:
3、波的图像与振动图像的比较
|
|
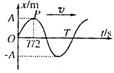
简谐运动的振图象 |
机械波的波动图象 |
|
|
图象 |
 |
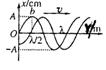 |
|
|
研究对象 |
一个振动质点 |
波传播方向所有质点 |
|
|
研究内容 |
一质点位移随时间变化规律 |
某时刻所有质点的空间分布规律 |
|
|
函数关系 |
一个质点做简谐运动时,它的位置x随时间t变化的关系 |
在某一时刻某一直线上各个质点的位置所形成的图象(横波) |
|
|
坐标 |
横轴 |
一个质点振动的时间 |
各质点平衡位置距坐标原点的位置(距离) |
|
纵轴 |
一个质点不同时刻相对平衡位置的位移 |
同一时刻各质点相对各自平衡位置的位移 |
|
|
形状 |
正弦函数或余弦函数的图象 |
||
|
由图象可直观得到的数据 |
周期T 振幅A |
波长λ 振幅A 波峰及波谷的位置 |
|
|
物理意义 |
表示一质点在各时刻的位移 |
表示某时刻各质点的位移 |
|
|
图象变化 |
随时间推移图象延续,但已有形态不变 |
随时间推移,图象沿传播方向平移 |
|
|
完整曲线占横坐标距离 |
表示一个周期 |
表示一个波长 |
|
|
图象上某一点的物理意义 |
在某时刻(横轴坐标)做简谐运动的物体相对平衡位置的位移(纵轴坐标) |
在某时刻,距坐标原点的距离一定(横轴坐标)的该质点的位移(纵坐标) |
2、机械波:基本概念,形成条件
特点:传播的是振动形式和能量,介质的各质点只在平衡位置附近振动并不随波迁移。
①各质点都作受迫振动, ②起振方向与振源的起振方向相同, ③离源近的点先振动,④没波传播方向上两点的起振时间差=波在这段距离内传播的时间 ⑤波源振几个周期波就向外传几个波长
波长的说法:①两个相邻的在振动过程中对平衡位置“位移”总相等的质点间的距离.②一个周期内波传播的距离
③两相邻的波峰(或谷)间的距离.④过波上任意一个振动点作横轴平行线,该点与平行线和波的图象的第二个交点之间的距离为一个波长. ⑤波从一种介质传播到另一种介质,频率不改变,
波长、波速、频率的关系: V=lf =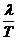 (适用于一切波)
(适用于一切波)
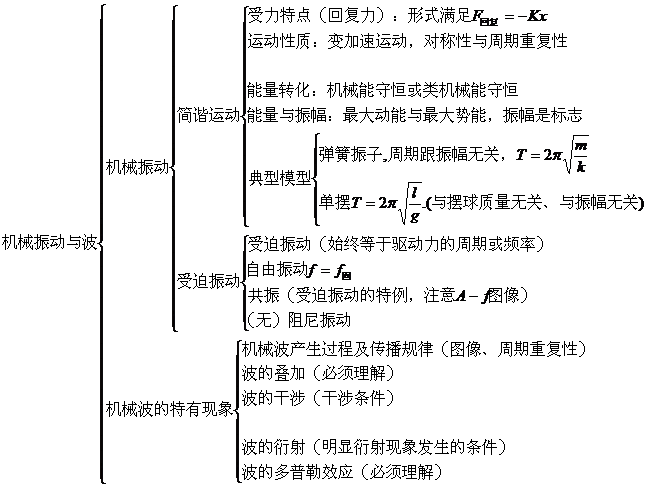 二、难点与突破
二、难点与突破
1、振动
(1)简谐运动:简谐运动中的力学运动学条件及位移,回复力,振幅,周期,频率及在一次全振动过程中各物理量的变化规律。
简谐振动: 回复力: F = 一KX 加速度:a =一KX/m
单摆:T= 2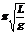 (与摆球质量,振幅无关) *弹簧振子T= 2
(与摆球质量,振幅无关) *弹簧振子T= 2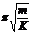 (与振子质量有关,与振幅无关)
(与振子质量有关,与振幅无关)
等效摆长、等效的重力加速度 影响重力加速度有:
①纬度,离地面高度
②在不同星球上不同,与万有引力圆周运动规律(或其它运动规律)结合考查
③系统的状态(超、失重情况)
④所处的物理环境有关,有电磁场时的情况
⑤静止于平衡位置时等于摆线张力与球质量的比值
注意等效单摆(即是受力环境与单摆的情况相同)
(2)共振的现象、条件、防止和应用
16、解析:设冰壶在未被毛刷擦过的冰面上滑行的距离为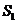 ,所受摩擦力的大小为
,所受摩擦力的大小为 :在 被毛刷擦过的冰面上滑行的距离为
:在 被毛刷擦过的冰面上滑行的距离为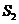 ,所受摩擦力的大小为
,所受摩擦力的大小为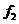 。则有
。则有
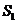 +
+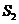 =S ①
=S ①
式中S为投掷线到圆心O的距离。
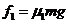 ②
②
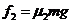 ③
③
设冰壶的初速度为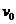 ,由功能关系,得
,由功能关系,得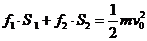 ④
④
联立以上各式,解得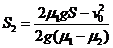 ⑤
⑤
代入数据得
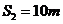 ⑥
⑥
15、解析:设物块到达劈A的低端时,物块和A的的速度大小分别为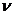 和V,由机械能守恒和动量守恒得
和V,由机械能守恒和动量守恒得
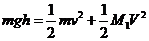 ①
①
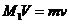 ②
②
设物块在劈B上达到的最大高度为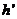 ,此时物块和B的共同速度大小为
,此时物块和B的共同速度大小为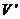 ,由机械能守恒和动量守恒得
,由机械能守恒和动量守恒得
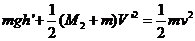 ③
③
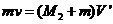 ④
④
联立①②③④式得
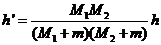 ⑤
⑤
14、解析:⑴设AB碰撞后的速度为v1,AB碰撞过程由动量守恒定律得
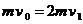
设与C碰撞前瞬间AB的速度为v2,由动能定理得
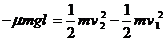
联立以上各式解得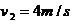
⑵若AB与C发生完全非弹性碰撞,由动量守恒定律得
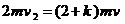
代入数据解得 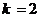
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得
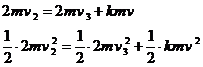
联立以上两式解得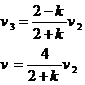
代入数据解得 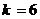
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得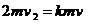
代入数据解得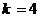
总上所述得 当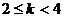 时,AB的运动方向与C相同
时,AB的运动方向与C相同
当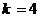 时,AB的速度为0
时,AB的速度为0
当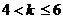 时,AB的运动方向与C相反
时,AB的运动方向与C相反
13、
解析:
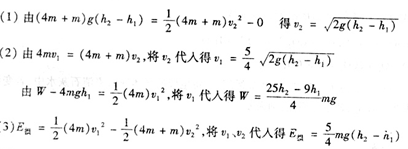
12、解析:
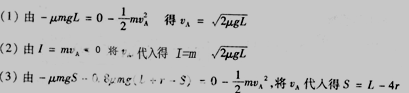
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com