5.某校准备参加2008年全国高中数学联赛，把10个名额分配给高三年级8个班，每班至少1人，不同的分配方案有_______种.

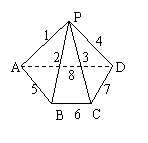
4. (2005江苏) 四棱锥的8条棱代表8种不同的化工产品，有公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共顶点的两条棱代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，那么安全存放的不同方法种数为　　　　　　　 (　 )

A．96　　　　 B.48　　　　 C.24　　　　 D.0

3.有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是　　　　　 (　 )

A.234　 　　　　 B.346　 　　　　 C.350　 　　　　　　　 D.363

2．(2006北京)在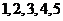这五个数字组成的没有重复数字的三位数中，各位数字之和为奇数的共有　　　　　　　　　　　　　　　　　　　 　　　　　　　(　 )

A.36个　　　 B.24个　　 C.18个　　　　　 D.6个

1．(2005湖北文)把一同排6张座位编号为1，2，3，4，5，6的电影票全部分给4个人，每人至少分1张，至多分2张，且这两张票具有连续的编号，那么不同的分法种数是　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　(　 )

A．168　　　　　　　　　　 B．96　　　　　　　　　　　 C．72　　　　　　　　　　　 D．144

8.错位法：编号为1至n的n个小球放入编号为1到 n的n个盒子里,每个盒子放一个小球要求小球与盒子的编号都不同,这种排列称为错位排列特别当n=2,3,4,5时的错位数各为1,2,9,44关于5、6、7个元素的错位排列的计算，可以用剔除法转化为2个、3个、4个元素的错位排列的问题：

7.分组、分配法：

分组问题(分成几堆,无序).有等分、不等分、部分等分之别。一般地平均分成n堆(组)，必须除以n!, 如果有m堆(组)元素个数相等，必须除以m！

例如：6本不同的书分成三组，分别是1本、2本、3本，共有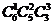 =60种分法；

6本不同的书分成三组，每组2本，共有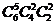÷3！=15种分法；

6本不同的书分成三组，分别是1本、1本、4本，共有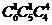÷2！=15种分法；

分配问题(有序分组):逐个分给.

例如:7本不同的书,分给甲、乙、丙三个人,依次得3、2、2本，有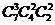 =210种分法。

如果不明确谁得3本,谁得2本呢?(先分组再分配,或先确定确定得3个球,再逐个分)

6.插板法：n个 相同元素,分成m(m≤n)组,每组至步一个的分组问题--把n个元素排成一的排,从n-1个空中选m-1个空,各插一个隔板,有.

例如:n个相同的小球分给m个人,每人至少一个小球的分法有种分法.

如果没有“每人至少一个”的限制,则需设想“每人先献出一个小球”,再对n+m个小球用“插板法”,有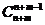种.

5.插空法:某些元素不相邻的排列.可以先排其它元素然,再让不相邻的元素插空;

4.捆绑法:某些元素必相邻的排列.可以先将相邻的元素“捆成一个”元素,与其它元素进行排列，然后再再给那“一捆元素”内部排列.