
3.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
( C )
A.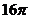 B.
B.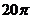 C.
C.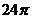 D.
D.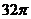
2.过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°则该截面的面积是 ( A )
A.π B.2π
C. 3π D.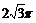
1.正方体的内切球与其外接球的体积之比为 ( C )
A.1∶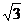 B.1∶3
C.1∶3
B.1∶3
C.1∶3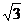 D.1∶9
D.1∶9
10.如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,∠BAC=60°,且SA⊥BC.
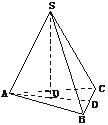
(1)求证:S-ABC为正三棱锥;
(2)已知SA=a,求S-ABC的全面积.
(1)证明:正棱锥的定义中,底面是正多边形;顶点在底面上的射影是底面的中心,两个条件缺一不可.作三棱锥S-ABC的高SO,O为垂足,连结AO并延长交BC于D.
因为SA⊥BC,所以AD⊥BC.
又侧棱与底面所成的角都相等,从而O为△ABC的外心,OD为BC的垂直平分线,
所以AB=AC.
又∠BAC=60°,故△ABC为正三角形,且O为其中心.所以S-ABC为正三棱锥.
(2)解:只要求出正三棱锥S-ABC的侧高SD与底面边长,则问题易于解决.
在Rt△SAO中,由于SA=a,∠SAO=60°,所以SO=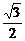 a,AO=
a,AO=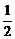 a.
a.
因O为重心,所以AD=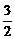 AO=
AO=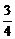 a,BC=2BD=2ADcot60°=
a,BC=2BD=2ADcot60°=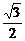 a,OD=
a,OD=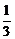 AD=
AD=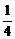 a.
a.
在Rt△SOD中,SD2=SO2+OD2=(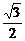 a)2+(
a)2+(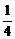 a)2=
a)2=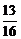 ,则SD=
,则SD=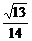 a.
a.
于是,(SS-ABC)全=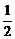 ·(
·(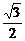 a)2sin60°+3·
a)2sin60°+3·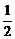 ·
· a·
a·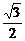 a=
a=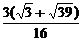 a2.
a2.
考查棱柱、棱锥的侧面积及体积的计算方法.要求会用棱柱、棱锥的侧面积及体积公式求棱柱、棱锥的侧面积及体积,会运用“分解与组合”(即“割补法”)、“等积变形”等方法,使问题化繁为简,化难为简,化未知为已知.
求体积常见方法有:①直接法(公式法);②分割法;③补形法.
9.已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
解法一:连结A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,
∵EF∥A1C1,∴A1C1∥平面B1EDF.
∴C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.
∵平面B1D1D⊥平面B1EDF,
∴O1H⊥平面B1EDF,即O1H为棱锥的高.
∵△B1O1H∽△B1DD1,∴O1H=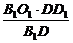 =
=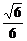 a,
a,
V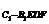 =
=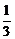 S
S ·O1H=
·O1H=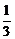 ·
·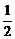 ·EF·B1D·O1H=
·EF·B1D·O1H=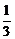 ·
·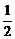 ·
·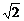 a·
a·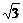 a·
a·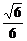 a=
a=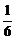 a3.
a3.
解法二:连结EF,设B1到平面C1EF的距离为h1,D到平面C1EF的距离为h2,则h1+h2=B1D1=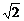 a,∴V
a,∴V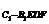 =V
=V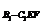 +V
+V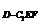 =
=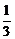 ·S
·S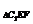 ·(h1+h2)=
·(h1+h2)=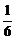 a3.
a3.
解法三:V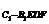 =V
=V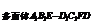 -V
-V -V
-V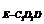 =
=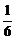 a3.
a3.
8.长方体的表面积为32cm2,体积为8 cm2,长、宽、高成等比数列,则长方体所有棱之和为_____ _____.32cm
7.已知正四棱锥的体积为12,底面对角线的长为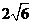 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。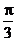
6.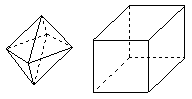 两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
( D )
两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
( D )
A.1个 B.2个 C.3个 D.无穷多个
5.已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则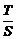 等于
(
A )
等于
(
A )
A.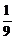 B.
B.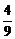 C.
C.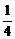 D.
D.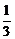
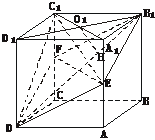
4. 如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF
如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF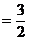 ,EF与面AC的距离为2,则该多面体的体积为
( D )
,EF与面AC的距离为2,则该多面体的体积为
( D )
A.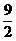 B.5
C.6 D.
B.5
C.6 D.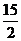
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com