
2.已知不等式x2+px+q<0的解集为{x| 1<x<2},则不等式 >0的解集为
>0的解集为
(A)(1, 2) (B)(-∞, -1)∪(1, 2)∪(6, +∞)
(C)(-1, 1)∪(2, 6) (D)(-∞, -1)∪(6, +∞)
1.不等式(x2-2x-3)(x2-4x+4)<0的解集为
(A){x| x<-1或x>3} (B){x| -1<x<3}
(C){x| x<-3或x>1} (D){x| -1<x<2或2<x<3}
12.如图,半径为2的半球内有一内接正六棱锥 ,则此正六棱锥的侧面积是________.
,则此正六棱锥的侧面积是________.
解:显然正六棱锥 的底面的外接圆是球的一个大圆,于是可求得底面边长为2,又正六棱锥
的底面的外接圆是球的一个大圆,于是可求得底面边长为2,又正六棱锥 的高依题意可得为2,依此可求得
的高依题意可得为2,依此可求得
考查球的概念及性质.要求要求会用球的表面积、体积公式求球的表面积、体积,会解决一些球与柱、锥的组合的简单的几何体问题.
11. 已知
已知 三点在球心为
三点在球心为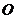 ,半径为
,半径为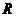 的球面上,
的球面上, ,且
,且 那么
那么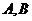 两点的球面距离为_______________,球心到平面
两点的球面距离为_______________,球心到平面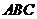 的距离为______________.
的距离为______________.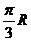 ,
, .
.
10.圆 是以
是以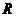 为半径的球
为半径的球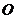 的小圆,若圆
的小圆,若圆 的面积
的面积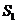 和球
和球 的表面积
的表面积 的比为
的比为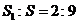 ,则圆心
,则圆心 到球心
到球心 的距离与球半径的比
的距离与球半径的比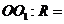 _____。1 : 3
_____。1 : 3
8.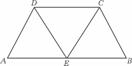 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为 ( C
)
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为 ( C
)
A.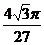 B.
B.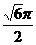 C.
C.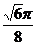 D.
D.
 9)如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是
( B )
9)如图,O是半径为l的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别是大圆弧AB与AC的中点,则点E、F在该球面上的球面距离是
( B )
A.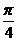 B.
B. C.
C.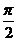 D.
D.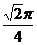
7.已知球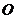 的半径是1,
的半径是1,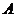 、
、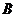 、
、 三点都在球面上,
三点都在球面上,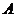 、
、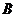 两点和
两点和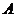 、
、 两点的球面距离都是
两点的球面距离都是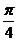 ,
,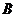 、
、 两点的球面距离是
两点的球面距离是 ,则二面角
,则二面角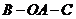 的大小是 ( C )
的大小是 ( C )
A.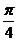 B.
B. C.
C.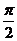 D.
D.
6.表面积为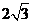 的正八面体的各个顶点都在同一个球面上,则此球的体积为 ( A )
的正八面体的各个顶点都在同一个球面上,则此球的体积为 ( A )
A.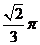 B.
B. C.
C. D.
D.
5.已知正方体外接球的体积是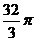 ,那么正方体的棱长等于
( D )
,那么正方体的棱长等于
( D )
A.2 B.
B. C.
C. D.
D.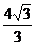
4.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为 ( A )
A. B. C. D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com