
5.(2008·山东文)设函数f(x)=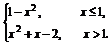 则f(
则f(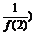 的值为 .
的值为 .
答案 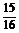
4.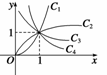 如图所示,曲线是幂函数y=xn在第一象限的图象,已知n取±2、±
如图所示,曲线是幂函数y=xn在第一象限的图象,已知n取±2、±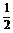 四个值,则相应的曲线C1,C2,C3,C4的n值依次为
.
四个值,则相应的曲线C1,C2,C3,C4的n值依次为
.
答案 2,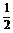 ,-
,-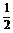 ,-2
,-2
3.如果幂函数y=(m2-3m+3)x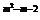 的图象不过原点,则m的取值是 .
的图象不过原点,则m的取值是 .
答案 1或2
2.幂函数f(x)=x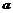 (
(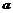 是有理数)的图象过点(2,
是有理数)的图象过点(2,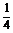 ),则f(x)的一个单调递减区间是 .
),则f(x)的一个单调递减区间是 .
答案 (0,+∞)
1.设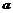 ∈{-1,1,
∈{-1,1,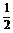 ,3},则使函数y=x
,3},则使函数y=x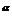 的定义域为R且为奇函数的所有的
的定义域为R且为奇函数的所有的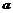 值为
.
值为
.
答案 1,3
24.(2006年全国理综1)(19分)一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ.初始时,传送带与煤块都是静止的.现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下一段黑色痕迹后,煤块相对于传送带不再滑动.求此黑色痕迹的长度.
解:根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0。根据牛顿定律,可得
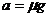 ①
①
设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有
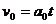 ②
②
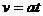 ③
③
由于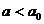 ,故
,故 ,煤块继续受到滑动摩擦力的作用。再经过时间
,煤块继续受到滑动摩擦力的作用。再经过时间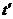 ,煤块的速度由v增加到v0,有
,煤块的速度由v增加到v0,有
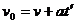 ④
④
此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹。
设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s,有
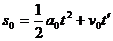 ⑤
⑤
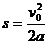 ⑥
⑥
传送带上留下的黑色痕迹的长度
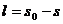 ⑦
⑦
由以上各式得
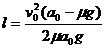 ⑧
⑧
评分参考:①式1分,②、③、④式各2分,⑤式4分,⑥式3分,⑦式1分,⑧式4分
23.(2005年北京理综)(16分)AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示,一小球自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小球的质量为m,不计各处摩擦.求:
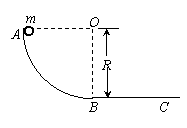 (1)小球运动到B点时的动能;
(1)小球运动到B点时的动能;
(2)小球下滑到距水平轨道的高度为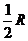 时速度的大小和方向;
时速度的大小和方向;
(3)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力Na、Nb各是多大?
解:(1)根据机械能守恒得:
(2)根据机械能守恒得: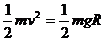
小球的速度沿圆弧的切线向下,与竖直方向成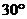
(3)根据牛顿运动定律在B点有: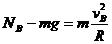
由A到B根据机械能守恒定律: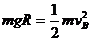
解得: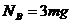
在C点小球平衡: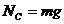
(2005年理综③) 24.(19分)如图所示,在倾角为θ的光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d. 重力加速度为g.
24.(19分)如图所示,在倾角为θ的光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为mA、mB,弹簧的劲度系数为k,C为一固定挡板.系统处于静止状态.现开始用一恒力F沿斜面方向拉物块A使之向上运动,求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d. 重力加速度为g.
解:令x1表示未加F时弹簧的压缩量,由胡克定律和牛顿定律得:

令x2表示未加B刚要离开C时弹簧的伸长量,a表示此时A的加速度,由胡克定律和牛顿定律得:
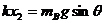

因此,物块B刚要离开C时物块A的加速度a为:
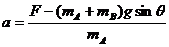
由题意得物块A的位移d为: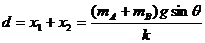
(2006年全国理综2)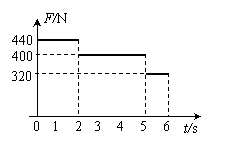 24.(19分)一质量为m=40kg的小孩子站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?取重力加速度g=10m/s2.
24.(19分)一质量为m=40kg的小孩子站在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?取重力加速度g=10m/s2.
解:由图可知,在t=0到t=2s的时间内,体重计的示数大于mg,故电梯应做向上的加速运动。设这段时间内电梯和小孩的加速度为a1,由牛顿第二定律
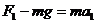 ,得:a1=1m/s2
,得:a1=1m/s2
在这段时间内电梯上升的高度为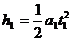 =2m
=2m
到t=2s的时间末电梯达到的速度为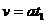 =2m/s
=2m/s
在t=2s到t=5s的时间内,体重计的示数等于mg,故电梯应向上的加做匀速运动。
在这段时间内电梯上升的高度为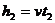 =6m
=6m
在t=5s到t=65s的时间内,体重计的示数小于mg,故电梯应向上的加做匀减速运动。设这段时间内电梯和小孩的加速度为a2,由牛顿第二定律
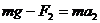 ,得:a2=2m/s2
,得:a2=2m/s2
在这段时间内电梯上升的高度为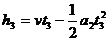 =1m
=1m
所以电梯在这段时间内上升的高度是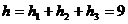 m
m
(2006年广东物理)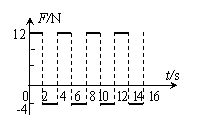 15.(14分)一个质量为4kg的物体放在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1,从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示,求83s内物体的位移大小和力F对物体所做的功.g=10m/s2
15.(14分)一个质量为4kg的物体放在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1,从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示,求83s内物体的位移大小和力F对物体所做的功.g=10m/s2
解:物体所受的摩擦力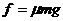
在每个周期内的前2s,物体运动的加速度大小为: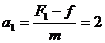 m/s2
m/s2
后2s,物体运动的加速度大小为: m/s2
m/s2
由于a1=a2,经过2s的加速,速度达到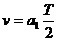 =4m/s,再经后2s减速为零。
=4m/s,再经后2s减速为零。
物体在一个周期内的位移为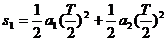 =8m
=8m
物体在82s内的位移为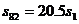 =164m
=164m
在第83s内,物体的速度由v=4m/s减为v/=2m/s,发生的位移为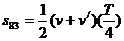 =3m
=3m
所以83s内物体的位移大小为s=167m
由动能定理,此过程中拉力F做功为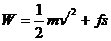 =676J
=676J
(2006年上海物理) 21.(l2分)质量为10kg的物体在F=200N的水平推力作用下,从粗糙斜面的底端由静止开始沿斜面运动,斜面固定不动,与水平地面的夹角θ=37O.力F作用2s后撤去,物体在斜面上继续上滑了1.25s后速度减为零.求:物体与斜面间的动摩擦因数μ和物体的总位移s.(已知sin37o=0.6,cos37O=0.8,g=10m/s2)
21.(l2分)质量为10kg的物体在F=200N的水平推力作用下,从粗糙斜面的底端由静止开始沿斜面运动,斜面固定不动,与水平地面的夹角θ=37O.力F作用2s后撤去,物体在斜面上继续上滑了1.25s后速度减为零.求:物体与斜面间的动摩擦因数μ和物体的总位移s.(已知sin37o=0.6,cos37O=0.8,g=10m/s2)
解:设物体在推力作用下(时间t1)的加速度为a1,撤去推力后(时间t2)的加速度为a2,则有: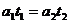
根据牛顿第二定律: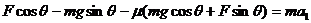
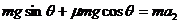
解得:μ=0.25
物体的总位移 =16.25m
=16.25m
(2004年全国理综1) 25.(20分)一小圆盘静止在桌布上,位于一方桌的水平桌面的中央.桌布的一边与桌的AB边重合,如图.已知盘与桌布间的动摩擦因数为μ1,盘与桌面间的动摩擦因数为μ2.现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边.若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
25.(20分)一小圆盘静止在桌布上,位于一方桌的水平桌面的中央.桌布的一边与桌的AB边重合,如图.已知盘与桌布间的动摩擦因数为μ1,盘与桌面间的动摩擦因数为μ2.现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边.若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)
答案:设圆盘的质量为m,桌长为l,在桌布从圆盘下抽出的过程中,圆盘的加速度为a1,有:μ1mg = ma1 ①
桌布抽出后盘子在桌面上做匀减速运动,以a2表示盘子的加速度的大小,有:μ2mg = ma2 ②
设圆盘刚离开桌布时的速度为v1,移动的距离为x1,离开桌布后在桌面上再移动距离x2后便停下,有:
υ12 =2a1x1 ③
υ12 =2a2x2 ④
盘没有从桌面上掉下的条件是x2≤1 l -x1 ⑤
设桌布从圆盘下抽出所经历的时间为t,在这段时间内桌布移动的距离为x,有:
对桌布x= 1 at2 ⑥
对盘 x1 = 1 a1t2 ⑦
而 x= 1 l + x1 ⑧
由以上各式解得:a≥( μ1 + 2 μ2) μ1g/ μ2 ⑨
21.(2000年上海物理)(12分)风洞实验室中可以产生水平方向的、大小可调节的风力,现将一套有小球的细直杆放入风洞实验室,小球孔径略大于细杆直径。
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上作匀速运动,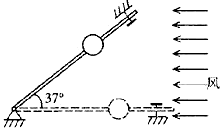 这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的滑动摩擦因数。
这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的滑动摩擦因数。
(2)保持小球所受风力不变,使杆与水平方向间夹角为37°并固定,则小球从静止出发在细杆上滑下距离S所需时间为多少?(sin37°=0.6,cos37°=0.8)
答案:(1)设小球所受的风力为F,小球质量为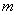
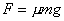
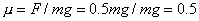
(2)设杆对小球的支持力为N,摩擦力为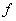
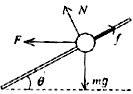 沿杆方向
沿杆方向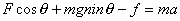
垂直于杆方向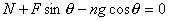
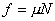
可解得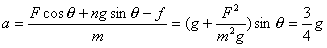
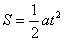
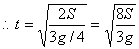
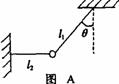
(2001年上海物理)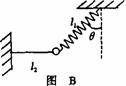 20.(10分)如图A所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,11的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态.现将l2线剪断,求剪断瞬时物体的加速度.
20.(10分)如图A所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,11的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态.现将l2线剪断,求剪断瞬时物体的加速度.
 (1)下面是某同学对该题的一种解法:
(1)下面是某同学对该题的一种解法:
解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在三力作用下保持平衡T1cosθ=mg,T1sinθ=T2,T2=mgtgθ,剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.
因为mgtgθ=ma,所以加速度a=gtgθ,方向在T2反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2)若将图A中的细线l1改为长度相同、质量不计的轻弹簧,如图B所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtgθ,你认为这个结果正确吗?请说明理由.
答案:(1)错。
因为I2被剪断的瞬间,l1上的张力大小发生了变化。
(2)对。
因为G被剪断的瞬间,弹簧U的长度末及发生变化,乃大小和方向都不变。
评分标准:全题10分。第(1)小题6分,第(2)小题4分。其中
(1)结论正确,得3分;评价和说明理由正确,得3分。
(2)结论正确,得2分;评价和说明理由正确,得2分。
(2003年江苏物理)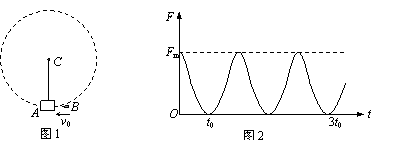 19.(13分)图1所示为一根竖直悬挂的不可伸长的轻绳,下端栓一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动. 在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图2所示.已知子弹射入的时间极短,且图2中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
19.(13分)图1所示为一根竖直悬挂的不可伸长的轻绳,下端栓一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动. 在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图2所示.已知子弹射入的时间极短,且图2中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
答案:由图2可直接看出,A、B一起做周期性运动,运动周期为T=2t0. 用m、m0分别表示A、B的质量,l表示绳长,v1、v2分别表示它们在圆周最低、最高点的速度,F1、F2分别表示运动到最低、最高点时绳的拉力大小,根据动量守恒有mv0=(m+m0)v1,根据牛顿定律有:F1-(m+m0)g=(m+m0) , F2+(m+m0)g=(m+m0) ,由机械能守恒又有:
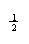 2l(m+m0)g= (m+m0)v12- (m+m0)v22,由图2知,F2=0,F1=Fm,由以上各式解得,反映系统性质的物理量是
2l(m+m0)g= (m+m0)v12- (m+m0)v22,由图2知,F2=0,F1=Fm,由以上各式解得,反映系统性质的物理量是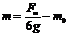 ,
,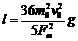 ,系统总机械能是E= (m+m0)v12,得E=3m02v02g/Fm
,系统总机械能是E= (m+m0)v12,得E=3m02v02g/Fm
46.(2002年上海综合)在水平路面上,一个大人推一辆重车,一个小孩推一辆轻车,各自作匀加速直线运动(阻力不计),甲、乙两同学在一起议论。甲两同学说:根据牛顿运动定律,大人的推力大,小孩的推力小,因此重车的加速度大。乙同学说:根据牛顿运动定律,重车质量大,轻车质量小,因此轻车加速度大。
你认为他们的说法是否正确?请简述理由。
26.(2001年上海综合)图中A为某火箭发射场,B为山区,C为城市。发射场正在进行某型号火箭的发射试验。该火箭起飞时质量为2.02×105kg,起飞推力2.75×106N,火箭发射塔高100m,则该火箭起飞时的加速度大小为 m/s2;在火箭推力不变的情况下,若不考虑空气阻力及火箭质量的变化,火箭起飞后,经
秒飞离火箭发射塔。(参考公式及常 数:F合=ma,vt=v0+at,S=v0t+(1/2)at2,g=9.8 m/s2)
数:F合=ma,vt=v0+at,S=v0t+(1/2)at2,g=9.8 m/s2)
答案:3.81米/秒2;7.25秒(答3.83秒同样给分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com