
3.与610°角终边相同的角表示为 .
答案 k·360°+250°(k∈Z)
2.若0<x<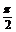 ,则sinx
,则sinx
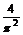 x2(用“>”,“<”或“=”填空).
x2(用“>”,“<”或“=”填空).
答案 >
1.已知cos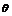 ·tan
·tan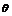 <0,那么角
<0,那么角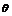 是第 象限角.
是第 象限角.
答案 三或四
12.已知函数f(x)=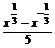 ,g(x)=
,g(x)=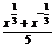 .
.
(1)证明f(x)满足f(-x)=-f(x),并求f(x)的单调区间;
(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,由此概括出涉及函数f(x)和g(x)的对所有
不等于零的实数x都成立的一个等式,并加以证明.
(1)证明 f(-x)=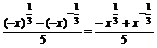 =-f(x),
=-f(x),
设x1>x2>0,由于y=x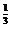 在R上递增,∴x
在R上递增,∴x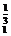 >x
>x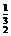 .又(x1x2)-
.又(x1x2)-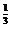 >0,
>0,
∴f(x1)-f(x2)=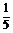 (x
(x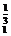 -x1
-x1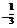 -x2
-x2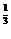 +
+ 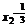 )=
)=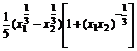 >0.
>0.
即f(x)在(0,+∞)上递增.
同理f(x)在(-∞,0)上也递增.
故f(x)在(-∞,0)和(0,+∞)上单调递增.
(2)解 f(4)-5f(2)g(2)=0,f(9)-5f(3)g(3)=0,
且f(x2)-5f(x)g(x)=0.
证明如下:
f(x2)-5f(x)g(x)=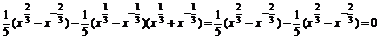
11.指出函数f(x)=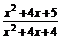 的单调区间,并比较f(-π)与f(-
的单调区间,并比较f(-π)与f(-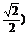 的大小.
的大小.
 解 ∵f(x)=
解 ∵f(x)=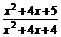 =1+
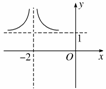
=1+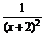 =1+(x+2)-2,其图象可由幂函数y=x-2向左平移2个单位,再向上平移1个单位,该函数在(-2,+∞)上是减函数,在(-∞,-2)上是增函数,且其图象关于直线x=-2对称(如图).
=1+(x+2)-2,其图象可由幂函数y=x-2向左平移2个单位,再向上平移1个单位,该函数在(-2,+∞)上是减函数,在(-∞,-2)上是增函数,且其图象关于直线x=-2对称(如图).
又∵-2-(-π)=π-2<-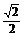 -(-2)=2-
-(-2)=2-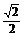 ,
,
∴f(-π)>f(-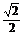 ).
).
10.已知f(x)=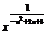 (n=2k,k∈Z)的图象在[0,+∞)上单调递增,解不等式f(x2-x)>f(x+3).
(n=2k,k∈Z)的图象在[0,+∞)上单调递增,解不等式f(x2-x)>f(x+3).
解 由条件知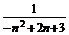 >0,
>0,
-n2+2n+3>0,解得-1<n<3.
又n=2k,k∈Z,∴n=0,2.
当n=0,2时,f(x)=x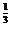 .∴f(x)在R上单调递增.
.∴f(x)在R上单调递增.
∴f(x2-x)>f(x+3)转化为x2-x>x+3.
解得x<-1或x>3.
∴原不等式的解集为(-∞,-1)∪(3,+∞).
9.求函数y=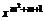 (m∈N)的定义域、值域,并判断其单调性.
(m∈N)的定义域、值域,并判断其单调性.
解 ∵m2+m+1=m(m+1)+1必为奇数,
且m2+m+1=(m+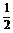 )2+
)2+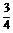 >0,
>0,
∴函数的定义域为R,
类比y=x3的图象可知,所求函数的值域为R,
在(-∞,+∞)上所求函数是单调递增函数.
8.给出封闭函数的定义:若对于定义域D内的任意一个自变量x0,都有函数值f(x0)∈D,则称函数y=f(x)在D上封闭.若定义域D=(0,1),则函数①f1(x)=3x-1;?②f2(x)=-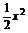 -
-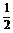 x+1;③f3(x)=1-x;④ f4(x)=x
x+1;③f3(x)=1-x;④ f4(x)=x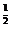 ,其中在D上封闭的是
.(填序号即可)
,其中在D上封闭的是
.(填序号即可)
答案 ②③④
7.当0<x<1时,f(x)=x2,g(x)=x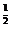 ,h(x)=x-2,则f(x),g(x),h(x)的大小关系是 .
,h(x)=x-2,则f(x),g(x),h(x)的大小关系是 .
答案 h(x)>g(x)>f(x)
6.设f(x)=x3+x,则对任意实数a,b,“a+b≥0”是“f(a)+f(b)≥0”的 条件.
答案 充分必要
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com