11．(12分)随着经济的持续发展，人民生活水平的不断提高，近年来我国私家车数量快速增长，高级和一级公路的建设也正加速进行．为了防止在公路弯道部分由于行车速度过大而发生侧滑，常将弯道部分设计成外高内低的斜面．如果某品牌汽车的质量为m，汽车行驶时弯道部分的半径为r，汽车轮胎与路面的动摩擦因数为μ，路面设计的倾角为θ，如图10所示．(重力加速度g取10 m/s²)

图10

(1)为使汽车转弯时不打滑，汽车行驶的最大速度是多少？

(2)若取sinθ＝，r＝60 m，汽车轮胎与雨雪路面的动摩擦因数为μ＝0.3，则弯道部分

汽车行驶的最大速度是多少？

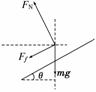解析：(1)受力分析如图所示，

竖直方向：

F_Ncosθ=mg+F_fsinθ；

水平方向：

F_Nsinθ+F_fcosθ=m ，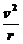

又F_f=μF_N，

可得v= .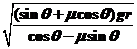

(2)代入数据可得：v=14.6 m/s.

答案：(1) 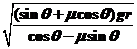　(2)14.6 m/s

10．(11分)(2008·广东高考)有一种叫“飞椅”的游乐项目，示意图如图9所示，长　

为L的钢绳一端系着座椅，另一端固定在半径为r的水平转盘边缘，转盘可绕

穿过其中心的竖直轴转动．当转盘以角速度ω匀速转动时，钢绳与转轴在同一

竖直平面内，与　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图9

竖直方向的夹角为θ，不计钢绳的重力，求转盘转动的角速度ω与夹角θ的关系．

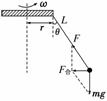解析：设座椅的质量为m，匀速转动时，座椅的运动半径为

R=r+Lsinθ　　　　　　　　　　　　　　　　　　　　　　 ①

受力分析如右图，由牛顿第二定律，有

F_合＝mgtanθ　　　　　　　　　　　　　　　　　　　　　　 ②

F_合＝mω²R　　　　　　　　　　　　　　　　　　　　　　 ③

联立①②③，得转盘角速度ω与夹角θ的关系

ω＝ .

答案：ω＝

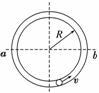
9．(2010·南通模拟)如图8所示，小球在竖直放置的光滑圆形管道内做圆周

运动，内侧壁半径为R，小球半径为r，则下列说法正确的是(　)

A．小球通过最高点时的最小速度v_min＝

B．小球通过最高点时的最小速度v_min＝0　　　　　　　　　　　　　　　　　 图8

C．小球在水平线ab以下的管道中运动时，内侧管壁对小球一定无作用力

D．小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力

解析：小球沿管上升到最高点的速度可以为零，故A错误，B正确；小球在水平线ab以下的管道中运动时，由外侧管壁对小球的作用力F_N与球重力在背离圆心方向的分力F_mg的合力提供向心力，即：F_N－F_mg＝m，因此，外侧管壁一定对球有作用力，而内侧壁无作用力，C正确；小球在水平线ab以上的管道中运动时，小球受管壁的作用力与小球速度大小有关，D错误．

答案：BC

8.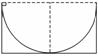如图7所示，一小物块在开口向上的半圆形曲面内以某一速率开始下　

滑，曲面内各处动摩擦因数不同，此摩擦作用使物块下滑时速率保持

不变，则下列说法正确的是　　　　　　　　　　　　　　　 (　)

A．因物块速率保持不变，故加速度为零　　　　　　　　　　　　　　　 图7

B．物块所受合外力大小不变，方向在变

C．在滑到最低点以前，物块对曲面的压力越来越大

D．在滑到最低点以前，物块受到的摩擦力越来越小

解析：物块速率不变，可理解为物块的运动是匀速圆周运动的一部分，物块所受合外力充当所需的向心力，故合外力大小不变，而方向在变，向心加速度不为零，A错，B对；对物块受力分析并正交分解可得F_N－mgcosθ＝m，而且其中θ越来越小，所以F_N越来越大；F_f＝mgsinθ，其中θ越来越小，所以F_f越来越小，C、D均正确．

答案：BCD

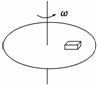
7.如图6所示，物块在水平圆盘上，与圆盘一起绕固定轴匀速运动，下列说

法中正确的是　　　　　　　　　　　　　　　　　　　　　 (　)

A．物块处于平衡状态

B．物块受三个力作用　　　　 　　　　　　　　　　　　　　　　　　　　　　图6

C．在角速度一定时，物块到转轴的距离越远，物块越容易脱离圆盘

D．在物块到转轴距离一定时，物块运动周期越小，越容易脱离圆盘

解析：对物块受力分析可知，物块受竖直向下的重力、垂直圆盘向上的支持力及指向圆心的摩擦力共三个力作用，合力提供向心力，A错，B正确．根据向心力公式F＝mrω²可知，当ω一定时，半径越大，所需的向心力越大，越容易脱离圆盘；根据向心力公式F＝mr()²可知，当物块到转轴距离一定时，周期越小，所需向心力越大，越容易脱离圆盘，C、D正确．

答案：BCD

6．铁路转弯处的弯道半径r是根据地形决定的．弯道处要求外轨比内轨高，其内外轨高度差h的设计不仅与r有关，还与火车在弯道上的行驶速率v有关．下列说法正确的是　　　　　

(　)

A．v一定时，r越小则要求h越大

B．v一定时，r越大则要求h越大

C．r一定时，v越小则要求h越大

D．r一定时，v越大则要求h越大

解析：设轨道平面与水平方向的夹角为θ，由mgtanθ＝m，得tanθ＝.可见v一定时，r越大，tanθ越小，内外轨道的高度差h越小，故A正确，B错误；当r一定时，v越大，tanθ越大，内外轨道的高度差越大，故C错误，D正确．

答案：AD

5.用一根细线一端系一小球(可视为质点)，另一端固定在一光滑圆锥顶上，　

如图4所示．设小球在水平面内做匀速圆周运动的角速度为ω，线的张力

为F_T，则F_T随ω²变化的图象是图5中的　　　　　　　　　　 (　) 　　　图4

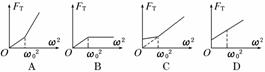
图5

解析：小球角速度ω较小，未离开锥面时，设线的张力为F_T，线的长度为L，锥面对小球的支持力为F_N，则有F_Tcosθ+F_Nsinθ＝mg，F_Tsinθ－F_Ncosθ＝mω²Lsinθ，可得出：F_T＝mgcosθ+mω²Lsin²θ，可见随ω由0开始增加，F_T由mgcosθ开始随ω²的增大，线性增大，当角速度增大到小球飘离锥面时，F_T·sinα＝mω²Lsinα，得F_T＝mω²L，可见F_T随ω²的增大仍线性增大，但图线斜率增大了，综上所述，只有C正确．

答案：C

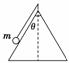
4.质量为60 kg的体操运动员做“单臂大回环”，用一只手抓住单杠，伸展

身体，以单杠为轴做圆周运动．如图3所示，此过程中，运动员到达最低

点时手臂受的拉力至少约为(忽略空气阻力，g＝10 m/s²)　　　　　 (　)

A．600 N　　　　 　B．2400 N　　　　　　　　　　　　　　　 图3

C．3000 N 　　　　　　　　　D．3600 N

解析：设运动员的重心到单杠的距离为R，在最低点的最小速度为v，则有mv²＝mg·2R

F－mg＝

由以上二式联立并代入数据解得F＝3000 N.

答案：C

3.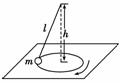用一根细绳，一端系住一个质量为m的小球，另一端悬在光滑水平桌面上方h处，绳长l大于h，使小球在桌面上做如图2所示的匀速圆周运动．若使小球不离开桌面，其转速最大值是　　　　　　　　　　　　　　　 (　)

A. 　　　　　　　 　B．π

C. 　 　　　　　　　　　D．2π 　　　　　　　　　　　　　　　 图2

解析：转速最大时，小球对桌面刚好无压力，

则F_向＝mgtanθ＝mlsinθω²，即ω＝ ，其中cosθ＝，所以n＝＝ ，

故选A.

答案：A

2.如图1所示，OO′为竖直轴，MN为固定在OO′上的水平光滑杆，　　

有两个质量相同的金属球A、B套在水平杆上，AC和BC为抗拉能力　

相同的两根细线，C端固定在转轴OO′上．当绳拉直时，A、B两球

转动半径之比恒为2∶1，当转轴的角速度逐渐增大时　　　 (　) 　　　　　图1

A．AC先断　　　　　　 　B．BC先断

C．两线同时断 　　　　　　　　D．不能确定哪段线先断

解析：A受重力、支持力、拉力F_A三个力作用，拉力的分力提供向心力，得：水平方向：F_Acosα＝mr_Aω²，

同理，对B：F_Bcosβ＝mr_Bω²，

由几何关系，可知cosα＝，cosβ＝.

所以：＝＝＝.

由于AC>BC，所以F_A>F_B，即绳AC先断．

答案：A