7．如图7所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P连接，P的斜面与固定挡板MN接触且处于静止状态，则斜面体P此刻所受的外力个数有可能为　　　　　　　　　　　　　　　　　　　　　 (　)

A．2个　　　　　B．3个

C．4个　 　　　　　　　　D．5个

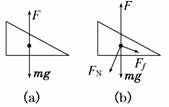解析：若斜面体P受到的弹簧弹力F等于其重力mg，则MN对P没

有力的作用，如图(a)所示，P受到2个力，A对；若弹簧弹力大于P

的重力，则MN对P有压力F_N，只有压力F_N则P不能平衡，一定存

在向右的力，只能是MN对P的摩擦力F_f，因此P此时受到4个力，

如图(b)所示，C对．

答案：AC

6.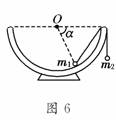如图6所示，一个半球形的碗放在桌面上，碗口水平，O点为其球　 心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m₁和m₂的小球，当它们处于 平衡状态时，质量为m₁的小球与O点的连线与水平线的夹角为α＝60°，则两小球的质量比为　　　　　　　　 (　)

A.　　　　　　　 　B.　　　　　　　　 C.　　　　　 　D.

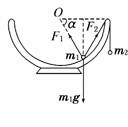
解析：质量为m₁的小球受重力m₁g、绳拉力F₂＝m₂g和支持力F₁的作用而平衡．如图所示，由平衡条件得，F₁＝F_2,2F₂cos30°＝m₁g，得＝.故选项A正确．

答案：A

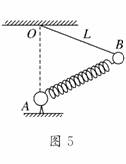
5．(2010·泰州模拟)如图5所示，A、B两球用劲度系数为k₁的轻弹簧相连，B球用长为L的细线悬于O点，A球固定在O点正下方，且O、A间的距离恰为L，此时绳子所受的拉力为F₁，现把A、B间的弹簧换成劲度系数为k₂的轻弹簧，仍使系统平衡，此时绳子所受的拉力为F₂，则F₁与F₂的大小关系为　　　　　　　　　　　　　　 (　)

A．F₁＜F₂ B．F₁＞F₂

C．F₁＝F₂ D．因k₁、k₂大小关系未知，故无法确定

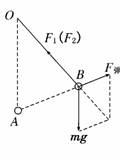解析：对B球受力分析如图所示，

则由相似三角形特点知：

＝＝

所以F₁＝F₂＝mg.

答案：C

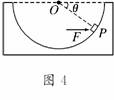
4. (2009·山东高考)如图4所示，光滑半球形容器固定在水平面上，O为球心．一质量为m 的小滑块，在水平力F的作用下静止于P点．设滑块所受支持力为F_N，OP与水平方向的夹角为θ.下列关系正确的是　　　　 　　(　)

A．F＝　　　B．F＝mgtanθ

C．F_N＝　 　　　　　D．F_N＝mgtanθ

解析：滑块受力如图，由平衡条件知：

＝cotθ⇒F＝mgcotθ＝，

F_N＝.

答案：A

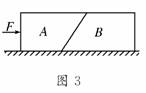
3.如图3所示，A、B两物体紧靠着放在粗糙水平面上，A、B间接触面光滑．在水平推力F 作用下两物体一起加速运动，物体A恰好不离开地面，则物体A的受力个数为　　　　　　　　　　 (　)

A．3　 　　　　B．4　　　　　 C．5　 　　　　　　　D．6

解析：A恰好不离开地面，即A与地面无作用力，故A受重力、F和B对A的作用力，共三个力，正确选项为A.

答案：A

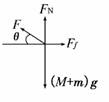
2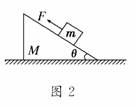．(2008·海南高考)如图2所示，质量为M的楔形物块静止在水平地面上，其斜面的倾角为θ.斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉小物块，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止．地面对楔形物块的支持力为　　　　　　　　　　　　　　　　　 　　　　　　(　)

A．(M+m)g　 　　　　　　　　　　B．(M+m)g－F

C．(M+m)g+Fsinθ　　　　　　 　D．(M+m)g－Fsinθ

解析：楔形物块静止，小物块匀速上滑，二者都处于平衡状态，取二者整体为研究对象，由受力分析得F_N+Fsinθ＝(M+m)g，所以F_N＝(M+m)g－Fsinθ，故选项D正确．

答案：D

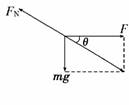
1．(2009·天津高考)物块静止在固定的斜面上，分别按如图1所示的方向对物块施加大小相等的力F，A中F垂直于斜面向上，B中F垂直于斜面向下，C中F竖直向上，D中F竖直向下，施力后物块仍然静止，则物块所受的静摩擦力增大的是　　　　　 (　)

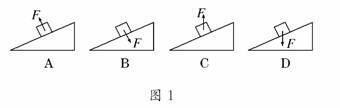
解析：物体在重力和F的合力沿斜面向下分力的作用下将受到沿斜面向上的静摩擦力，故知，竖直向下的力F会使其所受到的静摩擦力增大，D正确．

答案：D

12．(14分)(2010·淮安模拟)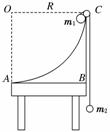如图10所示，半径为R的四分之一圆弧形支架竖直放置，圆弧边缘C处有一小定滑轮，绳子不可伸长，不计一切摩擦，开始时，m₁、m₂两球静止，且m₁＞m₂，试求：

(1)m₁释放后沿圆弧滑至最低点A时的速度．

(2)为使m₁能到达A点，m₁与m₂之间必须满足什么关系．

(3)若A点离地高度为2R，m₁滑到A点时绳子突然断开，则m₁落地点离　　

A点的水平距离是多少？　　　　　　　　　　　　　　　　　　　　　　　 图10

解析：(1)设m₁滑至A点时的速度为v₁，此时m₂的速度为v₂，由机械能守恒得：

m₁gR－m₂gR＝m₁v₁²+m₂v₂²

又v₂＝v₁cos45°

得：v₁＝ .

(2)要使m₁能到达A点，v₁≥0且v₂≥0，

必有：m₁gR－m₂gR≥0，得：m₁≥m₂.

(3)由2R＝gt²，x＝v₁t得x＝4R·.

答案：(1)

(2)m₁≥m₂　(3)4R·

11．(12分)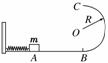如图9所示，光滑水平面AB与竖直面内的半圆形导轨在B点相接，导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半个圆周运动到达C点．试求：　　　　　 　　　　　　　　　　　　　　　　　　　　　　图9

(1)弹簧开始时的弹性势能；

(2)物体从B点运动至C点克服阻力做的功；

(3)物体离开C点后落回水平面时的动能．

解析：(1)物块在B点时，

由牛顿第二定律得：F_N－mg＝m，F_N＝7mg

E_kB＝mv_B²＝3mgR

在物体从A点至B点的过程中，根据机械能守恒定律，弹簧的弹性势能E_p＝E_kB＝3mgR.

(2)物体到达C点仅受重力mg，根据牛顿第二定律有

mg＝m

E_kC＝mv_C²＝mgR

物体从B点到C点只有重力和阻力做功，根据动能定理有：

W_阻－mg·2R＝E_kC－E_kB

解得W_阻＝－0.5mgR

所以物体从B点运动至C点克服阻力做的功为W＝0.5mgR.

(3)物体离开轨道后做平抛运动，仅有重力做功，根据机械能守恒定律有：

E_k＝E_kC+mg·2R＝2.5mgR.

答案：(1)3mgR　(2)0.5mgR　(3)2.5mgR

10.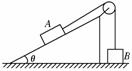 (11分)如图8所示，一固定的楔形木块，其斜面的倾角为θ＝30°，　

另一边与水平地面垂直，顶端有一个定滑轮，跨过定滑轮的细线　

两端分别与物块A和B连接，A的质量为4m，B的质量为m.开

始时，将B按在地面上不动，然后放开手，让A沿斜面下滑而B

上升，所有摩擦均忽略不计．当A沿斜面下滑距离x后，细线突然断了．求物块B上升

的最大高度H.(设B不会与定滑轮相碰)

解析：设细线断前一瞬间A和B速度的大小为v，A沿斜面下滑距离x的过程中，A的高度降低了xsinθ，B的高度升高了x.物块A和B组成的系统机械能守恒，物块A机械能的减少量等于物块B机械能的增加量，即

4mgxsinθ－·4mv²＝mgx+mv²

细线断后，物块B做竖直上抛运动，物块B机械能守恒，设物块B继续上升的最大高度为h，有mgh＝mv².

联立两式解得h＝，故物块B上升的最大高度为H＝x+h＝x+＝x.

答案：x