5. (2010·连云港模拟)一物体在A、B两点的正中间由静止开

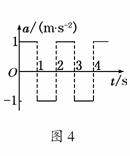
始运动(设不会超越A、B)，其加速度随时间变化如图4所示，

设指向A的加速度方向为正方向，若从出发开始计时，

则物体的运动情况是　　　　　　　　　　　　　 (　)

A．先向A运动，后向B，再向A，又向B,4 s末v＝0物体在原处

B．先向A运动，后向B，再向A，又向B,4 s末v＝0物体在偏向A的某点

C．先向A运动，后向B，再向A，又向B,4 s末v＝0物体在偏向B的某点

D．一直向A运动，4 s末v＝0物体在偏向A的某点

解析：各秒内加速度的大小均为1 m/s²，故各秒内均为匀变速直线运动，运动过程是先加速再减速，到0再加速后又减速到0，如此反复．

答案：D

4. (2008·宁夏高考)甲、乙两车在公路上沿同一方向做直线运动，它们的v－t图象如图3所示．两图象在t＝t₁时相交于P点，P在横轴上的投影为Q，△OPQ的面积为S.在t＝0时刻，乙车在甲车前面，相距为d.已知此后两车相遇两次，且第一次相遇的时刻为t′，则下面四组t′和d的组合可能的是　　　　　　　　　　　　　　　　　　　 (　)

A．t′＝t₁，d＝S　 B．t′＝t₁，d＝S

C．t′＝t₁，d＝S　 D．t′＝t₁，d＝S

解析：在t₁时刻如果甲车没有追上乙车，以

后就不可能追上了，故t′<t₁，A错；从图象

中甲、乙与坐标轴所围的面积即对应的位移看，甲在t₁时间内运动的位移比乙的多S，当t′＝0.5t₁时，甲的面积比乙的面积多出S，即相距d＝S，选项D正确．

答案：D

3．一列车队从同一地点先后开出n辆汽车在平直的公路上排成直线行驶，各车均由静止出发先做加速度为a的匀加速直线运动，达到同一速度v后改做匀速直线运动，欲使n辆车都匀速行驶时彼此距离均为x，则各辆车依次启动的时间间隔为(不计汽车的大小)

(　)

A. 　　　　　　　　B.　　　　　　　　　 C.　　　　　 　D.

解析：取相邻两车考虑：以后一辆车开始运动时为计时起点，设经时间t₀达到v做匀速运动，则前一辆车已经运动的时间为t₀+Δt.

前、后两车的位移分别为：

x_前＝t₀+vΔt

x_后＝t₀

由x_前－x_后＝x

t₀+vΔt－t₀＝x

得Δt＝.

答案：D

2．(2009·广东高考)图2所示是甲、乙两物体做直线运动的v－t图象．下列表述正确的是(　)

图2

A．乙做匀加速直线运动

B．0-1 s内甲和乙的位移相等

C．甲和乙的加速度方向相同

D．甲的加速度比乙的小

解析：甲、乙两物体在速度图象里的图形都是倾斜的直线，表明两物体都做匀变速直线运动，乙是匀加速，甲是匀减速，加速度方向不同，A对C错；根据在速度图象里面积表示位移的方法可知在0-1 s内甲通过的位移大于乙通过的位移，B错；根据斜率表示加速度可知甲的加速度大于乙的加速度，D错．

答案：A

1．(2010·徐州模拟)一质点自x轴原点出发，沿x轴正方向以

加速度a加速，经过t₀时间速度变为v₀，接着以－a加速度

运动，当速度变为－时，加速度又变为a，直至速度为时，

加速度再变为－a，直到速度变为－…，其v－t图象如图1

所示，则下列说法正确的是　　　　　　　　　　　　　　　　　 (　)

A．质点一直沿x轴正方向运动

B．质点将在x轴上一直运动，永远不会停止

C．质点最终静止时离开原点的距离一定大于v₀t₀

D．质点运动过程中离原点的最大距离为v₀t₀

解析：由v－t图可知，质点先沿x轴正向运动，经2t₀时间反向加速后减速，接着又正向加速后减速，如此反复，但每次位移总比前一次小，最终停止，质点在运动过程中在2t₀时刻离原点最远，其位移大小等于大三角形面积v₀·2t₀＝v₀t₀，只有D对．

答案：D

12．(15分)(2010·广州模拟)鸵鸟是当今世界上最大的鸟，有人说，如果鸵鸟能长出一副与身材大小成比例的翅膀，就能飞起来．生物学研究的结论指出：鸟的质量与鸟的体长立方成正比．鸟扇动翅膀，获得向上的升力的大小可以表示为F＝cSv²，式中S是翅膀展开后的面积，v为鸟的运动速度，c是比例常数．我们不妨以燕子和鸵鸟为例，假设鸵鸟能长出和燕子同样比例的大翅膀，已知燕子的最小飞行速度是5.5 m/s，鸵鸟的最大奔跑速度为22 m/s，又测得鸵鸟的体长是燕子的25倍，试分析鸵鸟能飞起来吗？

解析：燕子以最小速度飞行时，m₁g＝cS₁v₁².

而鸵鸟展翅以最大速度奔跑时，获得的升力为：

F₂＝cS₂v₂²

又＝25²，＝4，可得F₂＝10000 m₁g

而鸵鸟重力m₂g＝25³m₁g

故F₂＜m₂g，鸵鸟不能飞起来．

答案：鸵鸟不能飞起来

11．(15分)在倾角α＝37°的斜面上，一条质量不计的皮带一端固定在斜面上端，另一端绕过一质量m＝3 kg、中间有一圈凹槽的圆柱体，并用与斜面夹角β＝37°的力F拉住，使整个装置处于静止状态，如图11所示．不计一切摩擦，求拉力F和斜面对圆柱体的弹力F_N的大小．(g＝10 m/s² ，sin37°＝0.6，cos37°＝0.8)

某同学分析过程如下：

将拉力F沿斜面和垂直于斜面方向进行分解．

沿斜面方向：Fcosβ＝mgsinα

垂直于斜面方向：Fsinβ+F_N＝mgcosα

问：你认为上述分析过程正确吗？若正确，按照这种分析方法求出F及F_N的大小；

若不正确，指明错误之处并求出认为正确的结果．

解析：不正确，该同学没想到平行于斜面的皮带对圆柱体也有力的作用．

沿斜面方向：Fcosβ+F＝mgsinα

垂直于斜面方向：Fsinβ+F_N＝mgcosα

得：F＝ mg＝×30 N＝10 N

F_N＝mgcosα－Fsinβ＝30×0.8 N－10×0.6 N＝18 N.

答案：不正确　没想到平行于斜面的皮带对圆柱体也有力的作用　10 N　18 N

10．如图10所示，固定在水平面上的斜面倾角为θ，长方体木块A的质量为M，其PQ面上钉着一枚小钉子，质量为m的小球B通过一细线与小钉子相连接，细线与斜面垂直，木块与斜面间的动摩擦因数为μ，以下说法正确的是　　　　　　　　　　　　　　　 (　)

A．若木块匀速下滑，则小球对木块的压力为零

B．若木块匀速下滑，则小球对木块的压力为mgsinθ

C．若木块匀加速下滑，则小球对木块的压力为零

D．若木块匀加速下滑，则小球对木块的压力为μmgcosθ

解析：当木块匀速下滑时，对小球受力分析可求得小球对木块的压力为mgsinθ，B正确；当木块匀加速下滑时，将小球和木块看做一个整体，根据牛顿第二定律可得a＝gsinθ－μgcosθ，选小球为研究对象，可求得小球对木块的压力为μmgcosθ，D正确．

答案：BD

9.如图9所示，A是一质量为M的盒子，B的质量为，A、B用细绳相连，跨过光滑的定滑轮，A置于倾角θ＝30°的斜面上，B悬于斜面之外而处于静止状态．现在向A中缓慢加入沙子，整个系统始终保持静止，则在加入沙子的过程中　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．绳子拉力逐渐减小

B．A对斜面的压力逐渐增大

C．A所受的摩擦力逐渐增大

D．A所受的合力不变

解析：以B为研究对象，由二力平衡条件可知，绳子的拉力F_T始终等于B的重力的大小，即F_T＝Mg，选项A错误．以A为研究对象，未加沙子前，绳子拉力F_T与A的重力沿斜面方向的分力平衡，A与斜面间没有摩擦力的作用；加入沙子后，相当于A的重力增加，A对斜面的压力增大，为了平衡加入沙子的重力沿斜面方向的分力，A将受到沿斜面向上的静摩擦力，且随着沙子的加入而逐渐增大，所以选项B、C正确．因为A一直处于静止状态，所受的合力为零，保持不变，选项D正确．

答案：BCD

8．如图8所示，一倾角为45°的斜面固定于竖直墙上，为使一光滑的铁球静止，需加一水平力F，且F过球心，下列说法正确的是　　　　　 (　)

A．球一定受墙的弹力且水平向左

B．球可能受墙的弹力且水平向左

C．球一定受斜面的弹力且垂直斜面向上

D．球可能受斜面的弹力且垂直斜面向上

解析：对球受力分析，可以确定的力是水平力F和重力mg，根据平衡条　

件，斜面对球一定有弹力的作用，墙对球可能有弹力，也可能没有弹力．

答案：BC