
6.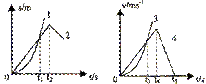 如图所示的位移(s)-时间(t)图象和速度(v)-时间(t)图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是 (
)
如图所示的位移(s)-时间(t)图象和速度(v)-时间(t)图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是 (
)
A.图线1表示物体做曲线运动
B.s-t图象中t1时刻v1>v2
C.v-t图象中0至t3时间内3和4的平均速度大小相等
D.两图象中,t2、t4时刻分别表示2、4开始反向运动
5.如图所示,真空中等量异种点电荷放置在M、N两点,在MN
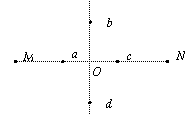 的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,
的连线上有对称点a、c,MN连线的中垂线上有对称点b、d,
则下列说法正确的是 ( )
A.a点场强与c点场强一定相同
B.a点电势一定小于c点电势
C.负电荷在c点电势能一定大于在a点电势能
D.正电荷从d点移到b点电场力不做功
4.如图是电熨斗的结构图,下列说法正确的是 ( )
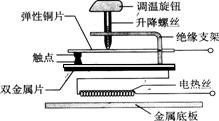
A.双金属片上层金属的膨胀系数小于下层金属
B.常温下,上下触点接触;温度过高时,双金属片发生弯曲使上下触点分离
C.需要较高温度熨烫时,要调节调温旋钮,使升降螺丝下移并推动弹性铜片下移
D.双金属片温度传感器的作用是控制电路的通断
3.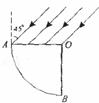 如图所示,空气中有一折射率为
如图所示,空气中有一折射率为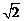 的玻璃柱体,其横截而是
的玻璃柱体,其横截而是
圆心角为90o,、半径为R的扇形OAB、一束平行光平行于
横截面,以45o入射角射到OA上,OB不透光,若考虑首
次入射到圆弧AB上的光,则圆弧AB上有光透出的部分
的弧长为 ( )
A.1/6 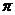 R B.1/4
R B.1/4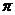 R
R
C.1/3 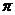 R D.5/12
R D.5/12 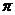 R
R
2.太阳因核聚变释放出巨大的能量,同时其质量不断减少。太阳每秒钟辐射出的能量约为4×1026J,根据爱因斯坦质能方程,太阳每秒钟减少的质量最接近 ( )
A.1036Kg B.1018Kg C.1013Kg D.109Kg
1.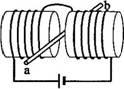 如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,
如图所示,两个端面半径同为R的圆柱形铁芯同轴水平放置,
相对的端面之间有一缝隙,铁芯上绕导线并与电源连接,在
缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中,
且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落,铜棒
下落距离为0.2R时铜棒中电动势大小为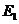 ,下落距离为0.8R时电动势大小为
,下落距离为0.8R时电动势大小为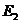 ,忽略涡流损耗和边缘效应.关于
,忽略涡流损耗和边缘效应.关于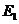 、
、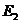 的大小和铜棒离开磁场前两端的极性,下列判断正确的是 ( )
的大小和铜棒离开磁场前两端的极性,下列判断正确的是 ( )
A.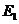 >
>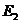 ,a端为正 B.
,a端为正 B.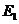 >
>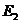 ,b端为正
,b端为正
C.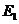 <
<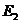 ,a端为正 D.
,a端为正 D.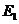 <
<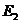 ,b端为正
,b端为正
3.三角恒等式的证明
证明三角恒等式的过程,实际上是化异为同的过程,即化去形式上的异,而呈现实质上的同,这个过程,往往是从化简开始的--这就是说,在证明三角恒等式时,我们可以从最复杂处开始.
例5 求证 cosα(2secα+tgα)(secα-2tgα)=2cosα-3tgα.
分析 从复杂的左边开始证得右边.
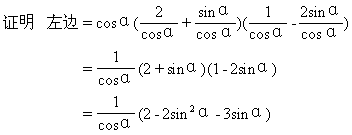
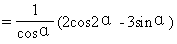
=2cosα-3tgα=右边
例6 证明恒等式
(1)1+3sin2αsec4α+tg6α=sec6α
(2)(sinA+ secA)3+(cosA+cscA)2=(1+secAcscA)2
分析 (1)的左、右两边均较复杂,所以可以从左、右两边同时化简
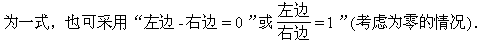
证明 (1)右边-左边=sec6α-tg6α-3sin2αsec4α-1
=(sec2α-tg2α)(sec4α+sec2α·tg2α+tg2α)-3sin2αsec4α-1
=(sec4α-2sec2αtg2α+tg2α)-1
=(sec2α-tg2α)2-1=0
∴等式成立.
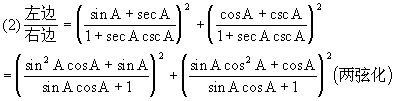
=sin2A+cos2A=1故原式成立
在解题时,要全面地理解“繁”与“简”的关系.实际上,将不同的角化为同角,以减少角的数目,将不同的函数名称,化为同名函数,以减少函数的种类,都是化繁为简,以上两点在三角变换中有着广泛的应用.
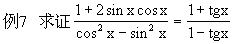
分析1 从右端向左端变形,将“切”化为“弦”,以减少函数的种类.
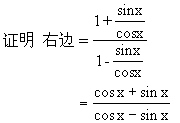
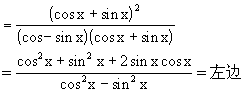
分析2 由1+2sinxcosx立即想到(sinx+cosx)2,进而可以约分,达到化简的目的.
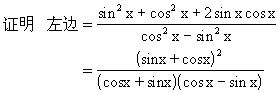
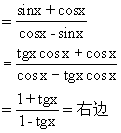
说明 (1)当题目中涉及多种名称的函数时,常常将切、割化为弦(如解法1),或将弦化为切(如解法2)以减少函数的种类.
(2)要熟悉公式的各种变形,以便迅速地找到解题的突破口,请看下列.
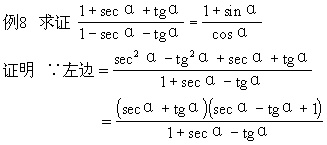
=secα+tgα
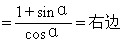
∴等式成立
说明 以上证明中采用了“1的代换”的技巧,即将1用sec2α-tg2α代换,可是解题者怎么会想到这种代换的呢?很可能,解题者在采用这种代换时,已经预见到代换后,分子可以因式分解,可以约分,而所有这一切都是建立在熟悉公式的各种变形的基础上的,当然,对不熟练的解题者而言,还有如下的“一般证法”--即证明“左边-右边=0”
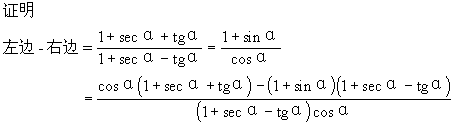
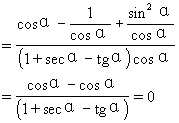
∴左边=右边
2.三角函数式的化简
三角函数式的化简的结果应满足下述要求:
(1)函数种类尽可能地少.
(2)次数尽可能地低.
(3)项数尽可能地少.
(4)尽可能地不含分母.
(5)尽可能地将根号中的因式移到根号外面来.
化简的总思路是:尽可能地化为同类函数再化简.
例3 化简sin2α·tgα+cos2α·ctgα+2sinαcosα
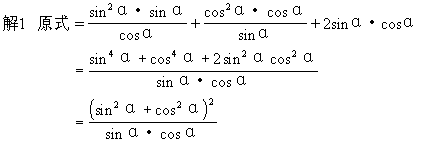
=secα·cscα
解2 原式=(sin2α·tgα+sinα·cosα)+(cos2α·ctgα+sinαcosα)
=tgα·(sin2α+cos2α)+ctgα(sin2α+cos2α)
=tgα+ctgα
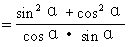
=secα·cscα
说明 (1)在解1中,将正切、余切化为正弦、余弦再化简,仍然是循着减少函数种类的思路进行的.
(2)解2中的逆用公式将sinα·cosα用tgα表示,较为灵活,解1与解2相比,思路更自然,因而更实用.
例4 化简:
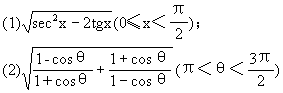
分析 将被开方式配成完全平方式,脱去根号,进行化简.
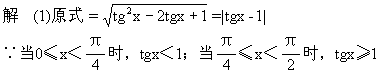
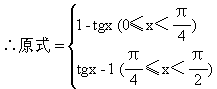
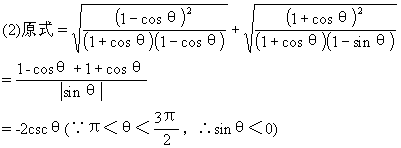
1.已知某角的一个三角函数值,求该角的其他三角函数值.
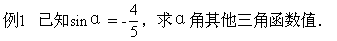
解 ∵sinα<0
∴角α在第三或第四象限(不可能在y轴的负半轴上)
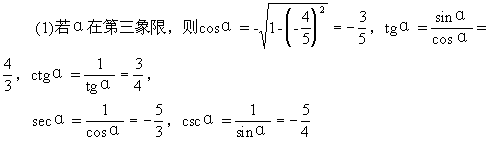
(2)若α在第四象限,则
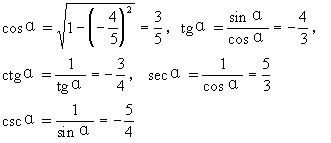
说明 在解决此类问题时,要注意:
(1)尽可能地确定α所在的象限,以便确定三角函数值的符号.
(2)尽可能地避免使用平方关系(在一般情况下只要使用一次).
(3)必要时进行讨论.
例2 已知sinα=m(|m|≤1),求tgα的值.
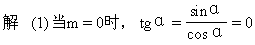
(2)当m=±1时,α的终边在y轴上,tgα无意义.
(3)当α在Ⅰ、Ⅳ象限时,∵cosα>0.
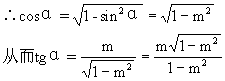
当α在第Ⅱ、Ⅲ象限时,∵cosα<0,
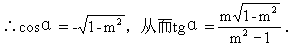
说明 (1)在对角的范围进行讨论时,不可遗漏终边在坐标轴上的情况.
(2)本题在进行讨论时,为什么以cosα的符号作为分类的标准,而不按sinα的符号(即m的符号)来分类讨论呢?你能找到这里的原因并概括出所用的技巧吗?
(三)实际运用,拓展延伸
 通过自行车模型,探究自行车的坐垫弹簧、减小与增大摩擦的应用。
通过自行车模型,探究自行车的坐垫弹簧、减小与增大摩擦的应用。
•多处刻有凹凸不平的花纹以增大摩擦。如车的外胎,车把手塑料套,蹬板套、闸把套等。
.变滚动摩擦为滑动摩擦以增大摩擦。如在刹车时,车轮不再滚动,而在地面上滑动,摩擦大大增加了,故车可迅速停驶。而在刹车的同时,手用力握紧车闸把,增大刹车皮对钢圈的压力以达到制止车轮滚动的目的。
•车的前轴、中轴及后轴均采用滚动以减小摩擦。为更进一步减小摩擦,人们常在这些部位加润滑剂。
•车的坐垫下安有许多根弹簧,利用它的弹性,发挥缓冲作用以减小震动。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com