6.若函数f(x)＝x³－3x+a有3个不同的零点，则实数a的取值范围是　　 (　)

A．(－2,2)　 　　　B．[－2,2]　　　 C．(－∞，－1)　 　　　D．(1，+∞)

解析：由f′(x)＝3x²－3＝3(x－1)(x+1)，

且当x＜－1时，f′(x)＞0；

当－1＜x＜1时，f′(x)＜0；当x＞1时，f′(x)＞0.

所以当x＝－1时函数f(x)有极大值，当x＝1时函数f(x)有极小值．

要使函数f(x)有3个不同的零点，只需满足

解之得－2＜a＜2.

答案：A

5.(文)函数f(x)＝x³+ax²+3x－9，已知f(x)在x＝－3时取得极值，则a＝　　　 (　)

A．2　　　 　B．3 　　　C．4 　　　　D．5

解析：因为f(x)＝x³+ax²+3x－9，所以f′(x)＝3x²+2ax+3，由题意有f′(－3)＝0，所以3×(－3)²+2a×(－3)+3＝0，由此解得a＝5.

答案：D

(理)设a∈R，若函数y＝e^x+ax，x∈R有大于零的极值点，则　　　　　　　 (　)

A．a＜－1　 　　B．a＞－1 　　　C．a＞－ 　　D．a＜－

解析：由y′＝(e^x+ax)′＝e^x+a＝0得e^x＝－a，

即x＝ln(－a)＞0⇒－a＞1⇒a＜－1.

答案：A

4．设函数f(x)＝x³+ax²－9x－1(a<0)．若曲线y＝f(x)的斜率最小的切线与直线12x+y＝6平行，求：

(1)a的值；

(2)函数f(x)的单调区间．

解：(1)因f(x)＝x³+ax²－9x－1，

所以f′(x)＝3x²+2ax－9

＝3²－9－.

即当x＝－时，f′(x)取得最小值－9－.

因斜率最小的切线与12x+y＝6平行，即该切线的斜率为－12，所以－9－＝－12，即a²＝9.

解得a＝±3，由题设a<0，所以a＝－3.

(2)由(1)知a＝－3，因此f(x)＝x³－3x²－9x－1，

f′(x)＝3x²－6x－9＝3(x－3)(x+1)，

令f′(x)＝0，解得x₁＝－1，x₂＝3.

当x∈(－∞，－1)时，f′(x)>0，

故f(x)在(－∞，－1)上为增函数；

当x∈(－1,3)时，f′(x)<0，

故f(x)在(－1,3)上为减函数；

当x∈(3，+∞)时，f′(x)>0，故f(x)在(3，+∞)上为增函数．

由此可见，函数f(x)的单调递增区间为(－∞，－1)和(3，+∞)，单调递减区间为(－1,3)．

3．已知函数y＝ax与y＝－在(0，+∞)上都是减函数，则函数y＝ax³+bx²+5的单调减区间为________．

解析：根据题意a＜0，b＜0.

由y＝ax³+bx²+5，得y′＝3ax²+2bx，

令y′＜0，可得x＞0或x＜－，

故所求减区间为(－∞，－)和(0，+∞)．

答案：(－∞，－)和(0，+∞)

2.若函数h(x)＝2x－+在(1，+∞)上是增函数，则实数k的取值范围是　　　 (　)

A．[－2，+∞)　　 　B．[2，+∞)　　　 C．(－∞，－2] 　　　D．(－∞，2]

解析：因为h′(x)＝2+，所以h′(x)＝2+＝≥0在(1，+∞)上恒成立，即k≥－2x²在(1，+∞)上恒成立，所以k∈[－2，+∞)．

答案：A

1.(2009·广东高考)函数f(x)＝(x－3)e^x的单调递增区间是说明　　　　　　　　　 (　)

A．(－∞，2)　 　　B．(0,3)　　 C．(1,4) 　　D．(2，+∞)

解析：f(x)＝(x－3)·e^x，f′(x)＝e^x(x－2)＞0，

∴x＞2.

∴f(x)的单调递增区间为(2，+∞)．

答案：D

20. 已知f(x)是定义域为(0，+∞)的函数，当x∈(0，1)时f(x)＜0．现针对任意正实数x、y，给出下列四个等式：

① f(xy)=f(x) f(y) ；② f(xy)=f(x)+f(y) ；③ f(x+y)=f(x)+f(y) ； ④ f(x+y)=f(x) f(y) ．

请选择其中的一个等式作为条件，使得f(x)在(0，+∞)上为增函数；并证明你的结论．

解：你所选择的等式代号是　　　　 　．　　　　　　　　　　　

19．已知二次函数.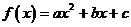

(1)若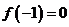，试判断函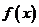数零点个数；

(2)若对任意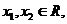且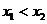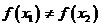，，试证明存在，

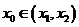使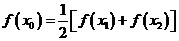成立．

18. 即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力，加速城市之间的流通；根据测算，如果一列火车每次拖4节车厢，每天能来回16次；如果每次拖7节车厢，则每天能来回10次；每天来回次数是每次拖挂车厢个数的一次函数，每节车厢一次能载客110人，试问每次应拖挂多少节车厢才能使每天营运人数最多？并求出每天最多的营运人数．(注：营运人数指火车运送的人数) .

17. 讨论函数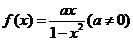在区间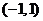上的单调性.