
1、 氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如下所示,在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )
氦原子被电离一个核外电子,形成类氢结构的氦离子,已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如下所示,在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )
A、40.8eV B、43.2eV C、51.0 eV D、54.4 eV
[例1]氢原子的核外电子从距核较近的轨道跃迁到距核较远的轨道的过程中( )
A、原子要吸收光子,电子的动能增大,原子的电势能增大
B、原子要放出光子,电子的动能减小,原子的电势能减小
C、原子要吸收光子,电子的动能增大,原子的电势能减小
D、原子要吸收光子,电子的动能减小,原子的电势能增大
[解析]根据玻尔理论,氢原子核外电子在离核越远的轨道上运动能量越大,必须吸收一定能量的光子后,电子才能从离核较近的轨道跃迁到离核较远的轨道,故B错。
氢原子核外电子绕核做圆周运动,由原子核对电子的库仑力提供其向心力,即
k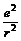 =m
=m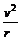 ,又Ek=
,又Ek= mv2,ke2/2r=
mv2,ke2/2r= mv2,即Ek=
mv2,即Ek=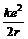 。
。
由此式可知:电子离核越远,r越大时,则电子的动能越小,故A、C错。
由于r变大时,库仑力对核外电子做负功,因此电势能增大,从而判断D正确。
[例2] Th(钍)经过一系列α和β衰变,变成
Th(钍)经过一系列α和β衰变,变成 Pb(铅),下列说法正确的是:
Pb(铅),下列说法正确的是:
A、铅核比钍核少8个质子
B、铅核比钍核少16个中子
C、共经过4次α衰变和6次β衰变
D、共经过6次α衰变和4次β衰变
[解析]由于β衰变不会引起质量数的减少,故可先根据质量数的减少确定α衰变的次数为:x= =6
=6
再结合核电荷数的变化情况和衰变规律来判定β衰变的次数y应满足:2x-y=90-82=8
所以y=2x-8=4
即答案D是正确的。
[例3]氢原子从能级A跃迁到能级B时,辐射出波长为λ1的光子,从能级A跃迁到能级C时,辐射出波长为λ2的光子,若λ1>λ2,则氢原子从能级B跃迁到能级C时,将吸收还是发射光子,光子的波长为多少?
[解析]因为EA-EB=h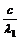 ,EA-EC=h
,EA-EC=h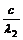 ,而λ1>λ2,所以EB>EC。
,而λ1>λ2,所以EB>EC。
于是从B能级跃迁到C能级时,应辐射光子。
EB-EC=(EA-EC)-(EA-EB)
=hc( -
-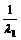 )=h
)=h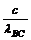
所以λBC=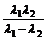 。
。
[例4]已知氘核质量为2.0136u,中子质量为1.0087u,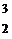 He核的质量为3.0150u。
He核的质量为3.0150u。
⑴写出两个氘核聚变成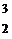 He的核反应方程;
He的核反应方程;
⑵计算上述核反应中释放的核能;
⑶若两氘核以相等的动能0.35MeV做对心碰撞即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的
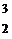 He核和中子的动能各是多少?
He核和中子的动能各是多少?
[解析]应用质量数守恒和核电荷数守恒不难写出核反应方程为: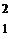 H+
H+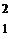 H→
H→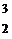 He+
He+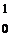 n
n
由题给条件可求出质量亏损为:
△m=2.0136u×2-(3.0150+1.0087)u=0.0035u
所以释放的核能为
△E=△mc2=931.5×0.0035MeV=3.26 MeV。
因为该反应中释放的核能全部转化为机械能--即转化为He核和中子的动能。若设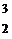 He核和中子的质量分别为m1、m2,速度分别为υ1、υ2,则由动量守恒及能的转化和守恒定律,得m1υ1-m2υ2=0
He核和中子的质量分别为m1、m2,速度分别为υ1、υ2,则由动量守恒及能的转化和守恒定律,得m1υ1-m2υ2=0
Ek1+ Ek2=2 Ek0+△E
解方程组,可得:
Ek1= (2Ek0+△E)=
(2Ek0+△E)= ×(2×0.35+3.26)MeV=0.99 MeV,
×(2×0.35+3.26)MeV=0.99 MeV,
Ek2=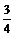 (2Ek0+△E)=
(2Ek0+△E)=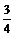 ×(2×0.35+3.26)MeV=2.97 MeV。
×(2×0.35+3.26)MeV=2.97 MeV。
6、能。6.86eV
原子和原子结构
5、⑴4.9×1014个 ⑵1.8×1017W
4、4.2×1021
3、A、B
2、B
1、B
6、已知锌板的极限波长λO=372nm,氢原子的基态能量为-13.6eV,若氢原子的核外电子从量子数n=2跃迁到n=1时所发出的光子照射到该锌板上,此时能否产生光电效应?若能,光电子的最大初动能是多少电子伏?(真空中光速c=3×108m/s,普朗克常量h=6.63×10-34J·s,电子电荷量e=1.6×10-19C)
课堂练习答案:
5、太阳光垂直射到地面上时,1m2地面接受的太阳光的功率为1.4kW,其中可见光部分约占45%。
⑴假如认为可见光的波长约为0.55μm,日地间距离R=1.5×1011m,普朗克恒量h=6.6×10-34J·s,估算太阳每秒辐射出的可见光光子为多少。
⑵若已知地球的半径r=6.4×106m,估算地球接受的太阳光的总功率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com