
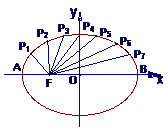
6.(2006四川15)如图把椭圆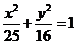 的长轴AB分成8份,过每个分点作x轴的垂线交椭圆的上半部分于
的长轴AB分成8份,过每个分点作x轴的垂线交椭圆的上半部分于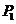 ,
,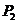 ,……
,……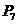 七个点,F是椭圆的一个焦点,则
七个点,F是椭圆的一个焦点,则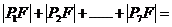 ____________.
____________.
简答提示:1-4.CBBA;
5.椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是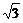 ,则这个椭圆方程为__________________.
,则这个椭圆方程为__________________.
4.设F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为 ( )
A. 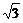 -1
B.2-
-1
B.2-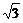 C.
C.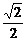 D.
D.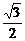
3. (2006山东)在给定椭圆中,过焦点且垂直于长轴的弦长为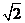 ,焦点到相应准线的距离为1,则该椭圆的离心离为
( )
,焦点到相应准线的距离为1,则该椭圆的离心离为
( )
A.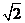 B.
B.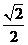 C.
C.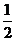 D.
D.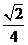
2.(2005广东) 若焦点在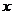 轴上的椭圆
轴上的椭圆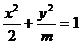 的离心率为
的离心率为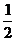 ,则m=(
)
,则m=(
)
A.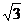 B.
B.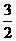 C.
C.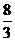 D.
D.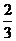
1.(2006全国Ⅱ)已知△ABC的顶点B、C在椭圆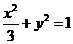 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 ( )
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 ( )
A. B.6
C.
B.6
C.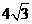 D.12
D.12
6.有关圆锥曲线弦的中点和斜率问题可利用“点差法”及结论:
设椭圆: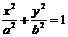 上弦AB的中点为M(x0,y0),则斜率kAB=
上弦AB的中点为M(x0,y0),则斜率kAB=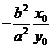 ,
,
对椭圆: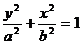 , 则kAB=
, 则kAB=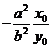 .
.
5.对椭圆方程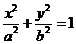 作三角换元即得椭圆的参数方程:
作三角换元即得椭圆的参数方程:
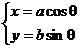 ;注意θ不是∠xOP(x,y).
;注意θ不是∠xOP(x,y).
4.椭圆方程中的a,b,c,e与坐标系无关,是椭圆本身所固有的,决定椭圆形状的参数,而焦点坐标,准线方程,顶点坐标,与坐标系有关.
3.性质:对于椭圆: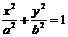 (a>b>0)如下性质必须熟练掌握:
(a>b>0)如下性质必须熟练掌握:
①范围; ②对称轴,对称中心; ③顶点;
④焦点; ⑤准线方程; ⑥离心率; (参见课本)
此外还有如下常用性质:
⑦焦半径公式: |PF1|=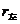 =a+ex0,|PF2|=
=a+ex0,|PF2|=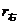 =a-ex0;(由第二定义推得)
=a-ex0;(由第二定义推得)
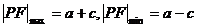
⑧焦准距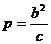 ;准线间距
;准线间距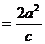 ;通径长
;通径长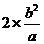 ;
;
⑨最大角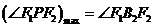
证:设|PF1|=r1,|PF2|=r2,则
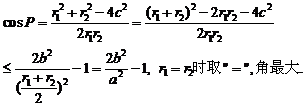
对于椭圆: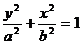 (a>b>0)的性质可类似的给出(请课后完成)。
(a>b>0)的性质可类似的给出(请课后完成)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com