
6.4棵柳树和4棵杨树栽成一行,柳树、杨树逐一相间的栽法有_____________种.
5.(2006春上海) 电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有 种不同的播放方式(结果用数值表示).
4.(2005全国II)在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有 个.
3. 若S=A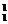 +A
+A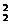 +A
+A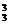 +A
+A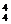 +…+A
+…+A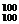 ,则S的个位数字是
,则S的个位数字是
A.8 B.5 C.3 D.0
2.2004黄冈检测)某班新年联欢会原定的6个节目已排成节目单,开演前又增加了3个新节目,如果将这3个节目插入节目单中,那么不同的插法种数为
A.504 B.210 C.336 D.120
1.某城市的电话号码,由六位升为七位(首位数字均不为零),则该城市可增加的电话部数是______ ( )
A.9×8×7×6×5×4×3 B.8×96
C.9×106 D.81×105
5.带限制条件排列问题
(1)限制条件的常见类型及解法:
某元素在不在某位置--优先按排受限制的元素或位置;
元素相邻--捆绑法,即把相邻元素看成一个元素;
元素不相邻--插空法;
数的大小,先考虑首位或前几位;整除问题,先看末位;
(2)一般思想方法:直接法,间接法,排除法,优先安排特殊元素或位置.务必做到分步清楚,分类明确,不重不漏.
4.排列:从n个不同的元素中取出m个(m≤n)元素并按一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
(1)排列数: 从n个不同的元素中取出m个(m≤n)元素的所有排列的个数.
(2)排列数公式:
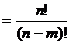 .
.
Ann=n!=n(n-1)! 规定 0!=1
3.两个计数原理的区别:
如果完成一件事,有n类办法,不论哪一类办法中的哪一种方法,都能独立完成这件事,用分类计数原理,
如果完成一件事需要分成几个步骤,各步骤都不可缺少,需要完成所有步骤才能完成这件事,是分步问题,用分步计数原理.
两个计数原理用来计算完成一件事的不同方法种数的,是计算排列组合,概率统计的基础,在生产,生活及科学实验中有广泛的应用.
2.分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有N=m1×m2×……mn 种不同的方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com