
3. 6个人并排站成一排,B站在A的右边,C站在B的右边,则不同的排法总数为
A. 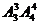 B.
B. 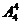 C.
C. 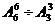 D.
D. 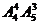 ( )
( )
[填空题]
2.若2n个学生排成一排的排法数为x,这2n个学生排成前后两排,每排各n个学生的排法数为y,则x、y的关系为 ( )
A.x>y B.x<y C.x=y D.x=2y
1.从长度分别为1、2、3、4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则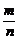 等于 ( )
等于 ( )
A.0 B. C.
C.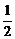 D.
D.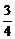
4.带有限制条件的排列问题的解题思想方法:
同步练习 10.1 计数原理 排列
[选择题]
3.正确理解排列的定义,掌握排列为公式:不仅与元素的异同有关,还与排放的位置、顺序有关。
2.正确区分两个原理:分类问题中,按一类中的每一种方法,做完后这件事就完成了;而分步问题中,必须把每一步都做完才算完成这件事。
1.分类计数原理和分步计数原理; 是解决排列、组合问题的算法基础.
[例1]从集合{1,2,3,…,10}中,选出由5个数组成的子集,使得这5个数中的任何两个数的和不等于11,这样的子集共有多少个?
解:和为11的数共有5组:1与10,2与9,3与8,4与7,5与6,子集中的元素不能取自同一组中的两数,即子集中的元素取自5个组中的一个数.而每个数的取法有2种,所以子集的个数为2×2×2×2×2=25=32.
提炼方法:解本题的关键是找出和为11的5组数,然后再用分步计数原理求解.
[例2]二次函数y=ax2+bx+c的系数a、b、c,在集合{-3,-2,-1,0,1,2,3,4}中选取3个不同的值,则可确定坐标原点在抛物线内部的抛物线多少条?
解:由图形特征分析,a>0,开口向上,坐标原点在内部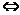 f(0)=c<0;a<0,开口向下,原点在内部
f(0)=c<0;a<0,开口向下,原点在内部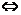 f(0)=c>0,所以对于抛物线y=ax2+bx+c来讲,原点在其内部
f(0)=c>0,所以对于抛物线y=ax2+bx+c来讲,原点在其内部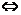 af(0)=ac<0,则确定抛物线时,可先定一正一负的a和c,再确定b,故满足题设的抛物线共有C
af(0)=ac<0,则确定抛物线时,可先定一正一负的a和c,再确定b,故满足题设的抛物线共有C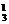 C
C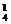 A
A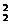 A
A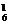 =144条
=144条
[例3]有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间,乙必在两端;
(2)甲不在左端,乙不在右端;
(3)男、女生分别排在一起;
(4)男女相间;
(5)甲、乙、丙三人从左到右顺序保持一定.
解:(1)优先安排特殊元素.乙的站法有2种,甲的站法有7种,其余随便站,共有:
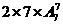 =70560种
=70560种
(2)按甲在不在右端分类分类讨论.
甲站右端的有: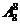 种;甲不在右端的有:
种;甲不在右端的有: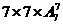 种;
种;
共有: 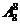 +
+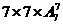 =
=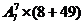 =287280种
=287280种
(3)(捆绑法)A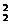 ·A
·A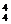 ·A
·A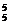 =5760种.
=5760种.
(4)(插空法)先排4名男生有A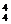 种方法,再将5名女生插空,有A
种方法,再将5名女生插空,有A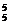 种方法,故共有A
种方法,故共有A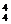 ·A
·A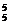 =2880种排法.
=2880种排法.
(5)方法一:(机会均等法)9人共有A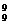 种排法,其中甲、乙、丙三人有A
种排法,其中甲、乙、丙三人有A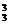 种排法,因而在A
种排法,因而在A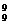 种排法中每A
种排法中每A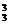 种对应一种符合条件的排法,故共有
种对应一种符合条件的排法,故共有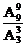 =60480种排法.
=60480种排法.
方法二:C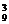 ·A
·A =60480种.
=60480种.
提炼方法:本题集排列多种类型于一题,充分体现了元素分析法(优先考虑特殊元素)、位置分析法(优先考虑特殊位置)、直接法、间接法(排除法)、捆绑法、机会均等法、插空法等常见的解题思路.
[例4]用0~9这十个数字组成没有重复数字的正整数
(1)共有几个三位数?
(2)求所有三位数的和;
(3)能被4整除的三位数有多少?
(4)比5231大的四位数有多少?
解:(1) 百位不能为 “0”,因此共有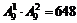 个;
个;
(2)考虑各数位上的数字之和,可得所有三位数的和为:
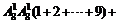
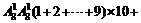
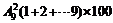
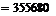
(3)只需考虑个,十两位能被4整除.,这两位能被4整除的数(含04,08)共有24个;
①含0的数有04、08、20、40、60、80,可组成能被4整除的三位数:6×8=48个
②不含0,且不重复数字的两位数有24-6-2=16个,可组成能被4整除的三位数:16×8=128个;
综上知,共可组成能被4整除的三位数:48+128=176个;
(4)①千位上为9,8,7,6的四位数各有A93个;②千位上是5,百位上为3,4,6,7,8,9的四位数各有A82个; ③千位上是5,百位上为2,十位上为4,6,7,8,9的四位数各有A71个; ④千位上是5,百位上为2,十位上为3且满足要求的共有5个,因此共有
N=4A93+6A82+5A71+5=2392种。
[研讨.欣赏]8个人站成一排,其中A、B、C互不相邻且D、E也互不相邻的排法有多少种?
解:先排去掉A、B、C外的5个人,有A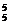 种,
种,
再排A、B、C 三人,有A63种.
故有A55·A63种(含D、E相邻).
其中D、E相邻的有A22·A44·A53种.
∴满足条件的排法种数为A55·A63-A22·A44·A53=11520.
8.(2006湖北)某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,又工程丁必须在工程丙完成后立即进行,那么安排这6项工程的不同排法种数是_____________.(用数字作答)
◆例题简答:1-3.DAC; 1.六位时,可装9×105部,七位时9×106.∴可增加9×106-9×105=81×105.答案:D; 2.A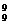 ÷A
÷A =504.答案:A; 3. A
=504.答案:A; 3. A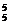 ,A
,A ,…中个位数字均为0,…; 4. 192; 5.
48; 6. 2A
,…中个位数字均为0,…; 4. 192; 5.
48; 6. 2A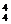 ·A
·A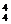 =1152种; 7. x=6或13(舍)。8. 20.
=1152种; 7. x=6或13(舍)。8. 20.
7.解方程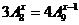 正整数x=______
正整数x=______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com