
3.(09·北京·14)下列现象中,与原子核内部变化有关的是 ( B )
A. 粒子散射现象
B.天然放射现象
粒子散射现象
B.天然放射现象
C.光电效应现象 D.原子发光现象
解析:α粒子散射实验表明了原子内部有一个很小的核,并没有涉及到核内部的变化,故A项错误;天然放射现象是原子核内部发生变化自发的放射出α粒子或电子,从而发生α衰变或β衰变,故B项正确;光电效应是原子核外层电子脱离原子核的束缚而逸出,没有涉及到原子核的变化,故C项错误;原子发光是原子跃迁形成的也没有涉及到原子核的变化,故D项错误。
2. (09·全国卷Ⅱ·18)氢原子的部分能级如图所示。已知可见光的光子能量在1.62eV到3.11eV之间。由此可推知, 氢原子
( AD
)
(09·全国卷Ⅱ·18)氢原子的部分能级如图所示。已知可见光的光子能量在1.62eV到3.11eV之间。由此可推知, 氢原子
( AD
)
A. 从高能级向n=1能级跃迁时了出的光的波长比可见光的短
B. 从高能级向n=2能级跃迁时发出的光均为可见光
C. 从高能级向n=3能级跃迁时发出的光的频率比可见光的高
D. 从n=3能级向n=2能级跃迁时发出的光为可见光
解析:本题考查玻尔的原理理论. 从高能级向n=1的能级跃迁的过程中辐射出的最小光子能量为9.20ev,不在1.62eV到3.11eV之间,A正确.已知可见光子能量在1.62eV到3.11eV之间从高能级向n=2能级跃迁时发出的光的能量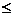 3.40ev,B错. 从高能级向n=3能级跃迁时发出的光的频率只有能量大于3.11ev的光的频率才比可见光高,C错.从n=3到n=2的过程中释放的光的能量等于1.89ev介于1.62到3.11之间,所以是可见光D对。
3.40ev,B错. 从高能级向n=3能级跃迁时发出的光的频率只有能量大于3.11ev的光的频率才比可见光高,C错.从n=3到n=2的过程中释放的光的能量等于1.89ev介于1.62到3.11之间,所以是可见光D对。
1.(09·全国卷Ⅰ·16) 氦氖激光器能产生三种波长的激光,其中两种波长分别为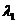 =0.6328µm,
=0.6328µm, =3.39µm,已知波长为
=3.39µm,已知波长为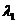 的激光是氖原子在能级间隔为
的激光是氖原子在能级间隔为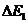 =1.96eV的两个能级之间跃迁产生的。用
=1.96eV的两个能级之间跃迁产生的。用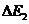 表示产生波长为
表示产生波长为 的激光所对应的跃迁的能级间隔,则
的激光所对应的跃迁的能级间隔,则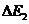 的近似值为
( D )
的近似值为
( D )
A.10.50eV B.0.98eV C.0.53eV D.0.36eV
解析:本题考查波尔的原子跃迁理论.根据 ,可知当
,可知当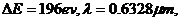 当
当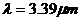 时,连立可知
时,连立可知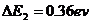 。
。
3.理解核能与核能的计算
凡是释放核能的核反应都有质量亏损。核子组成不同的原子核时,平均每个核子的质量亏损是不同的,所以各种原子核中核子的平均质量不同。核子平均质量小的,每个核子平均放的能多。铁原子核中核子的平均质量最小,所以铁原子核最稳定。凡是由平均质量大的核,生成平均质量小的核的核反应都是释放核能的。
核能的计算方法:
(1)根据爱因斯坦的质能亏损,用核子结合成原子核时的质量亏损(Δm)的千克数乘以真空中光速的平方(c=3×108m/s),即:ΔE=Δmc2 ①
(2)根据1原子质量单位(u)相当于931.5(MeV)能量,用核子结合成原子核时质量亏损的原子质量单位乘以931.5MeV,即:ΔE=Δm×931.5MeV ②
注意:
①式Δm的单位是千克(kg),ΔE的单位是焦耳(J);
②式中Δm的单位是指原子质量单位(u)(1u=1.660566×10-27 kg),
ΔE的单位是兆电子伏(MeV)。
(3)由核能的转化量来计算核能。
在无光子辐射的情况下,核反应中释放的核能转化为生成新核和新粒子的动能,因而在此情况下可应用力学原理--动量守恒和能量守恒来计算核能。
[例18] 一个氢原子的质量为1.6736×10-27kg,一个锂原子的质量为11.6505×10-27kg,一个氦原子的质量为6.6467×10-27kg。一个锂核受到一个质子轰击变为2个α粒子,⑴写出核反应方程,并计算该反应释放的核能是多少?⑵1mg锂原子发生这样的反应共释放多少核能?
解:⑴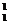 H+
H+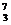 Li →2
Li →2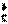 He 反应前一个氢原子和一个锂原子共有8个核外电子,反应后两个氦原子也是共有8个核外电子,因此只要将一个氢原子和一个锂原子的总质量减去两个氦原子的质量,得到的恰好是反应前后核的质量亏损,电子质量自然消掉。由质能方程ΔE=Δmc2得释放核能ΔE=2.76×10-12J
He 反应前一个氢原子和一个锂原子共有8个核外电子,反应后两个氦原子也是共有8个核外电子,因此只要将一个氢原子和一个锂原子的总质量减去两个氦原子的质量,得到的恰好是反应前后核的质量亏损,电子质量自然消掉。由质能方程ΔE=Δmc2得释放核能ΔE=2.76×10-12J
⑵1mg锂原子含锂原子个数为10-6÷11.6505×10-27,每个锂原子对应的释放能量是2.76×10-12J,所以共释放2.37×108J核能。
[例11]如下一系列核反应是在恒星内部发生的。
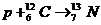
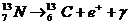
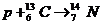

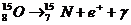

其中p为质子,α为α粒子,e+为正电子,γ为一种中微子,已知质子的质量为mp=1.672648×10-27kg,α粒子的质量为mα=6.644929×10-27kg,正电子的质量为me=9.11×10-31kg,中微子的质量可忽略不计,真空中的光速c=3×108m/s,试计算该系列核反应完成后释放的能量。
讲解:为求出该系列反应后释放的能量,将题中所给的诸核反应方程左右两侧分别相加,消去两侧相同的项,系列反应最终等效为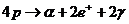 。
。
设反应后释放的能量为Q,根据质能关系和能量守恒得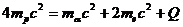 ,代入数值得Q=3.95×10-12J。
,代入数值得Q=3.95×10-12J。
[例19]在其他能源中,核能具有能量密度大,地区适应性强的优势。在核电站中,核反应堆释放的核能被转化为电能。核反应堆的工作原理是利用中子轰击重核发生裂变反应,释放出大量核能。
(1)核反应方程式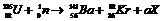 是反应堆中发生的许多核反应中的一种,X为待求粒子,a为X的个数,则X为 ,a=
。以mU、mBa、mKr分别表示
是反应堆中发生的许多核反应中的一种,X为待求粒子,a为X的个数,则X为 ,a=
。以mU、mBa、mKr分别表示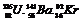 核的质量,mn、mp分别表示中子、质子的质量,C为光在真空中传播的速度,则在上述核反应过程中放出的核能ΔE= 。
核的质量,mn、mp分别表示中子、质子的质量,C为光在真空中传播的速度,则在上述核反应过程中放出的核能ΔE= 。
(2)有一座发电能力为P=1.00×106kW的核电站,核能转化为电能的效率η=40%。假定反应堆中发生的裂变反应全是本题(1)中的核反应,已知每次核反应过程放出的核能ΔE=2.78×10-11J, 核的质量mU=390×10-27kg。求每年(1年=3.15×107s)消耗的
核的质量mU=390×10-27kg。求每年(1年=3.15×107s)消耗的 的质量。
的质量。
分析与解 (1) 根据题意X为中子,a=3。质量亏损为mU-mBa-mKr-2mn,释放的核能为ΔE=(mU-mBa-mKr-2mn)c2
(2) 反应堆每年提供的核能为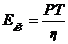 ,其中T表示一年的时间,以M表示每年消耗的
,其中T表示一年的时间,以M表示每年消耗的 的质量,则
的质量,则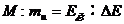 ,解上述式子可得
,解上述式子可得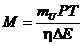 ,代入数据可以得到M=1.10×103 (kg)。
,代入数据可以得到M=1.10×103 (kg)。
[例20]太阳现正处于主序星演化阶段,它主要是由电子和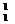 H、
H、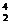 He等电子核组成,维持太阳辐射的是它内部的核聚变反应,核反应方程是2
He等电子核组成,维持太阳辐射的是它内部的核聚变反应,核反应方程是2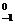 e+4
e+4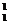 H→
H→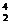 He+释放的核能,这些核能最后转化为辐射能,根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的
He+释放的核能,这些核能最后转化为辐射能,根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的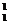 H核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段,为了简化,假定目前太阳全部由电子和
H核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段,为了简化,假定目前太阳全部由电子和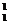 H核组成.
H核组成.
(1)为了研究太阳演化进程,需知道目前太阳的质量M,已知地球半径R=6.4×106 m,地球质量m=6.0×1024 kg,日地中心的距离r=1.5×1011 m,地球表面处的重力加速度g=10 m/s2,1年约为3.2×107 s,试估算目前太阳的质量M.
(2)已知质子质量mp=1.6726×10-27
kg,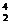 He质量mα=6.6458×10-27
kg,电子质量me=0.9×10-30 kg,光速c=3×108 m/s,求每发生一次题中所述的核聚变反应所释放的核能.
He质量mα=6.6458×10-27
kg,电子质量me=0.9×10-30 kg,光速c=3×108 m/s,求每发生一次题中所述的核聚变反应所释放的核能.
(3)又知地球上与太阳光垂直的每平方米截面上,每秒通过的太阳辐射能ω=1.35×103 W/m2,试估算太阳继续保持在主序星阶段还有多少年的寿命.(估算结果只需要一位有效数字)
[解析] (1)地球绕太阳的运动近似地认为是匀速圆周运动.由G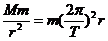 得:M=
得:M= .
.
又因为g=GM/R2所以M=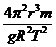 =2×1030
kg.
=2×1030
kg.
(2)ΔE=Δmc2=(2me+4mp-mα)c2=4.2×10-12 J.
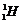 (3)太阳中 减少10%放出的总能量E=
(3)太阳中 减少10%放出的总能量E=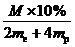 ·ΔE,太阳每秒辐射的总能量E′=4πr2ω,所以太阳保持在主序星阶段寿命t=E/E/=1010
年.
·ΔE,太阳每秒辐射的总能量E′=4πr2ω,所以太阳保持在主序星阶段寿命t=E/E/=1010
年.
到19世纪末,人们认识到物质由分子组成,分子由原子组成,原子由原子核和电子组成,原子核由质子和中子组成。
20世纪30年代以来,人们认识了正电子、μ子、K介子、π介子等粒子。后来又发现了各种粒子的反粒子(质量相同而电荷及其它一些物理量相反)。
现在已经发现的粒子达400多种,形成了粒子物理学。按照粒子物理理论,可以将粒子分成三大类:媒介子、轻子和强子,其中强子是由更基本的粒子--夸克组成。从目前的观点看,媒介子、轻子和夸克是没有内部结构的“点状”粒子。
用粒子物理学可以较好地解释宇宙的演化。
规律方法 1。掌握典型的反应方程
⑴衰变: α衰变: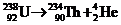 (核内
(核内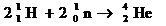 )
)
β衰变: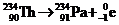 (核内
(核内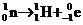 )
)
+β衰变: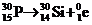 (核内
(核内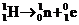 )
)
γ衰变:原子核处于较高能级,辐射光子后跃迁到低能级。
⑵人工转变: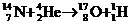 (发现质子的核反应)
(发现质子的核反应)
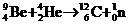 (发现中子的核反应)
(发现中子的核反应)
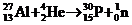
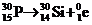 (人工制造放射性同位素)
(人工制造放射性同位素)
⑶重核的裂变: 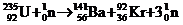 在一定条件下(超过临界体积),裂变反应会连续不断地进行下去,这就是链式反应。
在一定条件下(超过临界体积),裂变反应会连续不断地进行下去,这就是链式反应。
⑷轻核的聚变: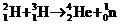 (需要几百万度高温,所以又叫热核反应)
(需要几百万度高温,所以又叫热核反应)
[例14] 完成下列核反应方程,并指出其中哪个是发现质子的核反应方程,哪个是发现中子的核反应方程。
 ⑵
⑵ 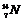 +
+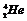 →
→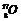 +_____
⑶
+_____
⑶ 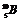 +
+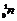 →_____+
→_____+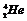
⑷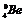 +
+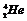 →_____+
→_____+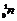 ⑸
⑸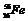 +
+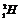 →
→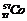 +_____
+_____
解:根据质量数守恒和电荷数守恒,可以判定:⑴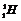 ,⑵
,⑵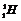 是发现质子的核反应方程,;⑶
是发现质子的核反应方程,;⑶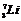 ,⑷
,⑷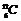 是发现中子的核反应方程; ⑸
是发现中子的核反应方程; ⑸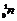
[例14])最近几年,原子核科学家在超重元素岛的探测方面取得重大进展。1996年科学家们在研究某两个重离子结合成超重元素的反应时,发现生成的超重元素的核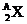 经过6次
经过6次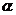 衰变后的产物是
衰变后的产物是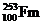 。由此,可以判定生成的超重元素的原子序数和质量数分别是
。由此,可以判定生成的超重元素的原子序数和质量数分别是
A.124、259 B.124、265 C.112、265 D.112、277
分析与解写出核反应方程为: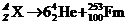 ,从而可知
,从而可知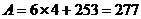 ,
,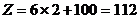 ,选项D正确。
,选项D正确。
[例15]
1956年李政道和杨振宁提出在弱相互作用中宇称不守恒,并由吴健雄用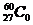 放射源进行了实验验证,次年,李、杨二人为此获得诺贝尔物理奖,
放射源进行了实验验证,次年,李、杨二人为此获得诺贝尔物理奖,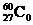 的衰变方程是
的衰变方程是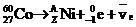 。其中
。其中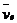 是反中微子,它的电荷为零,静止质量可认为是零
是反中微子,它的电荷为零,静止质量可认为是零
(1)CO与Fe同周期,它应在周期表的第_____周期,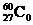 的核外电子数为____在上述衰变方程中,衰变产物
的核外电子数为____在上述衰变方程中,衰变产物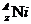 的质量数A是____,核电荷数Z是______。
的质量数A是____,核电荷数Z是______。
(2)在衰变前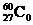 核静止,根据云室照片可以看出,衰变产物Ni和
核静止,根据云室照片可以看出,衰变产物Ni和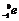 的运动径迹不在一条直线上,如果认为衰变产物只有Ni和
的运动径迹不在一条直线上,如果认为衰变产物只有Ni和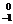 e,那么衰变过程将违背_____守恒定律。
e,那么衰变过程将违背_____守恒定律。
分析与解
(1) 关键要知道CO在周期表中的位置,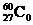 核外电子数等于质子数(27),而
核外电子数等于质子数(27),而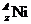 是
是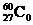 的衰变产物,且它与
的衰变产物,且它与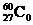 质量只相差一个电子和一个反中微子,电子质量仅为质子质量的
质量只相差一个电子和一个反中微子,电子质量仅为质子质量的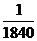 ,可忽略不计,又知道反中微子静止质量可认为是零。因此
,可忽略不计,又知道反中微子静止质量可认为是零。因此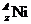 的质量数A应与
的质量数A应与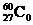 相同,也为60,据衰变方程知,
相同,也为60,据衰变方程知,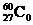 的一个中子变成质子,则
的一个中子变成质子,则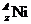 的电荷数应比
的电荷数应比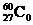 多1,即
多1,即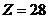 。
。
(2) 衰变前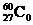 静止,总动量为零,衰变后若只产生两粒子
静止,总动量为零,衰变后若只产生两粒子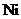 和
和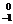 e,据动量守恒,
e,据动量守恒,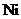 和
和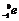 系统动量也为零,只有当两粒子运动在同一直线上,方向相反才能保持动量为零。假如原为静态粒子衰变为两个粒子,若现在它们却不在同一直线上运动,那肯定是违反了动量守恒定律。
系统动量也为零,只有当两粒子运动在同一直线上,方向相反才能保持动量为零。假如原为静态粒子衰变为两个粒子,若现在它们却不在同一直线上运动,那肯定是违反了动量守恒定律。
2.理解原子核的变化
无论天然放射性元素的衰变,还是原子核的人工转变,都遵循电荷数守恒、质量数守恒(注意:质量并不守恒),动量守恒与能量守恒有关规律,除去会写核反应过程以外,还需结合以前学过的力学知识、电磁学知识进行有关计算.
[例16] 静止的氡核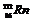 放出α粒子后变成钋核
放出α粒子后变成钋核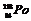 ,α粒子动能为Eα。若衰变放出的能量全部变为反冲核和α粒子的动能,真空中的光速为c,则该反应中的质量亏损为
,α粒子动能为Eα。若衰变放出的能量全部变为反冲核和α粒子的动能,真空中的光速为c,则该反应中的质量亏损为
A.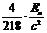 B. 0 C.
B. 0 C.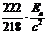 D.
D.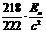
解:由于动量守恒,反冲核和α粒子的动量大小相等,由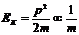 ,它们的动能之比为4∶218,因此衰变释放的总能量是
,它们的动能之比为4∶218,因此衰变释放的总能量是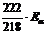 ,由质能方程得质量亏损是
,由质能方程得质量亏损是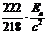 。
。
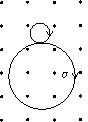 [例17] 静止在匀强磁场中的一个
[例17] 静止在匀强磁场中的一个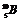 核俘获了一个速度为向v =7.3×104m/s的中子而发生核反应,生成α粒子与一个新核。测得α粒子的速度为2×104 m/s,方向与反应前中子运动的方向相同,且与磁感线方向垂直。求:⑴写出核反应方程。⑵画出核反应生成的两个粒子的运动轨迹及旋转方向的示意图(磁感线方向垂直于纸面向外)。⑶求α粒子与新核轨道半径之比。⑷求α粒子与新核旋转周期之比。
核俘获了一个速度为向v =7.3×104m/s的中子而发生核反应,生成α粒子与一个新核。测得α粒子的速度为2×104 m/s,方向与反应前中子运动的方向相同,且与磁感线方向垂直。求:⑴写出核反应方程。⑵画出核反应生成的两个粒子的运动轨迹及旋转方向的示意图(磁感线方向垂直于纸面向外)。⑶求α粒子与新核轨道半径之比。⑷求α粒子与新核旋转周期之比。
解:⑴由质量数守恒和电荷数守恒得: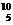 B+
B+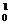 n→
n→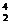 He+
He+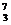 Li
Li
⑵由于α粒子和反冲核都带正电,由左手定则知,它们旋转方向都是顺时针方向,示意图如右。
⑶由动量守恒可以求出反冲核的速度大小是103m/s方向和α粒子的速度方向相反,由带电粒子在匀强磁场中做匀速圆周运动的半径公式r=mv/qB可求得它们的半径之比是120∶7
⑷由带电粒子在匀强磁场中做匀速圆周运动的周期公式T=2πm/qB可求得它们的周期之比是6∶7
2.轻核的聚变
①所谓轻核是指质量数很小的原子核,如氢核、氘核等.
②某些轻核结合成质量数较大的原子核的反应过程叫做轻核的聚变,同时放出大量的能量.
轻核聚变方程例举 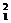 H+
H+ H→
H→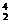 He+
He+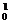 n
n
经核聚变只能发生在超高温(需要几百万度高温)条件下,故轻核聚变也叫做热核反应.
[例12]一个中子以1.9 ×107 m/s的速度射中一个静止的氮核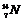 ,并发生核反应,生成甲、乙两种新核,它们的运动方向与中子原来的运动方向相同,测得甲核质量是中子质量的11倍,速度是1×106m/s,乙核垂直进入B=2 T的匀强磁场中做匀速圆周运动的半径为R=0.02 m,已知中子质量m=1.6×10-27kg,e=1.6×10-19C,求乙核是何种原子核?并写出核反应方程。
,并发生核反应,生成甲、乙两种新核,它们的运动方向与中子原来的运动方向相同,测得甲核质量是中子质量的11倍,速度是1×106m/s,乙核垂直进入B=2 T的匀强磁场中做匀速圆周运动的半径为R=0.02 m,已知中子质量m=1.6×10-27kg,e=1.6×10-19C,求乙核是何种原子核?并写出核反应方程。
[解析]设乙核质量为m乙,甲核质量为m甲=11m,氮核质量为14m。则由核反应过程中质量数守恒知,乙核质量数为:
14+1-11=4,即m乙=4m
由动量守恒定律: mv0== m甲v甲+ m乙v乙,
解得v乙=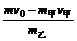 =2×l06m/s
=2×l06m/s
设乙核的电量为q,则由:R=mv/qB,得:q=m乙v/BR=3.2×10-19(C)=2e
[例12]众所周知,地球围绕着太阳做椭圆运动,阳光普照大地,万物生长。根据你学过的知以,试论述随着岁月的流逝,地球公转的周期,日地的平均距离及地球的表面温度变化的趋势。(不考虑流星及外星球与地球发生碰撞的可能性)。
[解析]太阳内部进行着激烈的热核反应,辐射大量光子,根据质能方程ΔE=Δm·C2,可知太阳的质量M在不断减小。由万有引力定律F=GMm/r2知,太阳对地球的万有引力也在不断减小。根据牛顿第二定律F=mv2/r知,日、地距离r将不断增大。由v=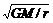 知,地球环绕太阳运动的速度将减小(或地球克服引力做功,动能减小),所以地球运行周期T=2πr/v将增大。由于太阳质量不断减小,辐射光子的功率不断减小,而r日地增大,所以辐射到地球表面热功率也不断减小。这样,地球表面温度也将逐渐降低。
知,地球环绕太阳运动的速度将减小(或地球克服引力做功,动能减小),所以地球运行周期T=2πr/v将增大。由于太阳质量不断减小,辐射光子的功率不断减小,而r日地增大,所以辐射到地球表面热功率也不断减小。这样,地球表面温度也将逐渐降低。
1.重核的裂变
①所谓重核即为质量数很大的原子核.
②重核俘获一个中子后分裂为两个或几个中等质量数的原子核的反应过程叫重核的裂变。在裂变的同时,还会放出几个中子和大量能量.
裂变方程式例举: 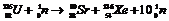
铀235裂变时,同时放出2-3个中子,如果这些中子再引起其他铀235核裂变,就可使裂变反应不断地进行下去,这种反应叫链式反应.铀235核能够发生接式反应的铀块的最小体积叫做它的临界体积.
③核反应堆的构造:
A.核燃料--用铀棒(含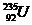 3%-4%的浓缩铀)。
3%-4%的浓缩铀)。
B.减速剂--用石墨、重水或普通水(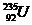 只吸收慢中子)。
只吸收慢中子)。
C.控制棒--用镉做成(镉吸收中子的能力很强)。
D.冷却剂--用水或液态钠(把反应堆内的热量传递出去)
2.核能
(1)结合能:核子结合成原子核时放出一定的能量,原子核分解成核子时吸收一定能量,这种能量叫结合能.
(2)质量亏损:核子结合生成原子核,所生成的原子核的质量比生成它的核子的总质量要小些,这种现象叫做质量亏损。
也可以认为.在核反应中,参加核反应的总质量m和核反应后生成的核总质量m/之差: Δm=m一m/
(3)爱因斯坦质能方程:爱因斯坦的相对论指出:物体的能量和质量之间存在着密切的联系,它们的关系是:E = mc2,这就是爱因斯坦的质能方程。
质能方程的另一个表达形式是:ΔE=Δmc2。
(4)核能计算:
①应用公式ΔE=Δmc 2时应选用国际单位,即ΔEM的单位为焦耳,Δm的单位为千克,C的单位为米/秒.
②1u相当于931.5MeV,其中u为原子质量单位:1u=1.660566×10-27kg ,lMev= l06 ev,leV=1.6×10-19J
③应用公式ΔE=931.5Δm时,ΔE的单位为兆电子伏(MeV),Δm的单位为原子质量单位.
[例10]下面是一核反应方程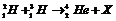 ,用
,用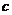 表示光速,则( )
表示光速,则( )
A. X是质子,核反应放出的能量等于质子质量乘C2
B. X是中子,核反应放出的能量等于质子质量乘C2
C. X是质子,核反应放出的能量等于氘核与氚核的质量和减去氦核与质子的质量和,再乘C2
D. X是中子,核反应放出的能量等于氘核与氚核的质量和减去氦核与中子的质量和,再乘C2
解:根据在核反应中,质量数和电荷数都守恒,可知核反应方程中的X为中子,根据爱因斯坦质能方程ΔE=Δmc2知,核反应放出的能量等于氘核与氚核的质量和减去氦核与中子的质量和,再乘以C2,答案为D。
1.核力:原子核的半径很小,其中的质子之间的库仑力很大,受到这么大的库仑斥力却能是稳定状态,一定还有另外一种力把各核子紧紧地拉在一起.这种力叫做核力
①核力是很强的力
②核力作用范围小,只在2.0×10-15 m短距离内起作用
③每个核子只跟它相邻的核子间才有核力作用
3.放射性同位素的应用
⑴利用其射线:α射线电离性强,用于使空气电离,将静电泄出,从而消除有害静电。γ射线贯穿性强,可用于金属探伤,也可用于治疗恶性肿瘤。各种射线均可使DNA发生突变,可用于生物工程,基因工程。
⑵作为示踪原子。用于研究农作物化肥需求情况,诊断甲状腺疾病的类型,研究生物大分子结构及其功能。
⑶进行考古研究。利用放射性同位素碳14,判定出土木质文物的产生年代。
一般都使用人工制造的放射性同位素(种类齐全,半衰期短,可制成各种形状,强度容易控制)。
[例9] 关于放射性同位素应用的下列说法中正确的有
A.放射线改变了布料的性质使其不再因摩擦而生电,因此达到消除有害静电的目的
B.利用γ射线的贯穿性可以为金属探伤,也能进行人体的透视
C.用放射线照射作物种子能使其DNA发生变异,其结果一定是成为更优秀的品种
D.用γ射线治疗肿瘤时一定要严格控制剂量,以免对人体正常组织造成太大的危害
解:利用放射线消除有害静电是利用放射线的电离性,使空气分子电离成为导体,将静电泄出。γ射线对人体细胞伤害太大,不能用来进行人体透视。作物种子发生的DNA突变不一定都是有益的,还要经过筛选才能培育出优秀品种。用γ射线治疗肿瘤对人体肯定有副作用,因此要科学地严格控制剂量。本题选D。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com