
6.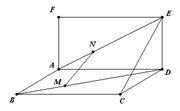 如图,已知矩形
如图,已知矩形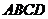 和矩形
和矩形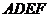 垂直,以
垂直,以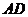 为公共边,但它们不在同一平面上.点M、N分别在对角线BD、AE上,且|BM|=
为公共边,但它们不在同一平面上.点M、N分别在对角线BD、AE上,且|BM|=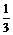 |BD|,|AN|=
|BD|,|AN|=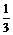 |AE|.证明:MN∥平面CDE.
|AE|.证明:MN∥平面CDE.
解:如图,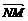 =
=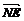 +
+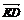 +
+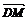 .
.
由已知,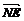 =
=
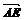 ,又因为
,又因为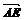 =
=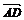 +
+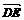 ,
,
所以 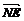 =
=
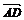 +
+
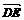 .
.
由已知,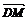 =
=
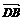 ,又因为
,又因为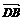 =
=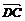 +
+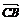 ,
,
所以 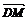 =
=
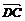 +
+
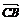 .所以
.所以 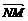 =
=
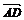 +
+
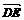 +
+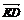 +
+
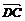 +
+
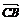 ,
,
又 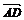 =-
=-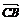 ,
,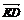 =-
=-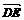 ,所以
,所以 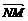 =
=
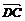 -
-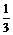
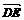 ,即有MN∥平面CDE.
,即有MN∥平面CDE.
5.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5):
(1)求以向量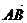 、
、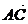 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
(2)若向量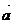 分别与向量
分别与向量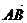 、
、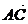 垂直,且|
垂直,且|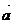 |=
|= ,求向量a的坐标。
,求向量a的坐标。
(1)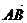 =(-2,-1,3),
=(-2,-1,3),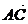 =(1,-3,2),
=(1,-3,2),
则cos∠BAC=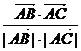 =
=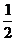 ,∴∠BAC=
,∴∠BAC=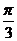 ,∴ S=|
,∴ S=|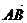 |·|
|·|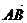 |·sin
|·sin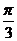 =7
=7
(2)设 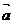 =(x,y,z),则
=(x,y,z),则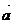 ⊥
⊥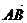
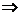 -2x-y+3z= 0
①
-2x-y+3z= 0
①
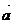 ⊥
⊥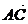
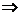 x-3y+2z=
0 ② |
x-3y+2z=
0 ② |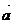 |=
|=
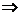 x2+y2+z2=3
③
x2+y2+z2=3
③
由式①、②、③解得,x=y=z=1 或 x=y=z=-1.
∴ 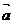 =(1,1,1)或
=(1,1,1)或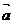 =(-1,-1,-1)
=(-1,-1,-1)
4.已知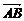 =(2,2,1),
=(2,2,1),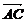 =(4,5,3),求平面ABC的单位法向量.
=(4,5,3),求平面ABC的单位法向量.
解:单位法向量n 0=±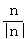 =±(
=±(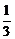 ,-
,-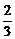 ,
,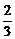 ).
).
3. 已知正四棱柱ABCD-A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点P为BD1中点. 证明EF为BD1与CC1的公垂线;
已知正四棱柱ABCD-A1B1C1D1.AB=1,AA1=2,点E为CC1中点,点P为BD1中点. 证明EF为BD1与CC1的公垂线;
证:建立如图的坐标系,得B(0,1,0),D1(1,0,2),F(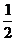 ,
,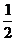 ,1),C1(0,0,2),E(0,0,1).
,1),C1(0,0,2),E(0,0,1).
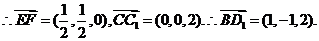
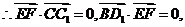 即EF⊥CC1,EF⊥BD1 .
即EF⊥CC1,EF⊥BD1 .
故EF是为BD1 与CC1的公垂线.
2.设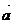 =(cosα,1,sinα),
=(cosα,1,sinα),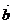 =(sinα,1,cosα),求证:(
=(sinα,1,cosα),求证:(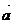 +
+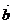 )⊥(
)⊥(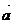 -
-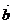 )。
)。
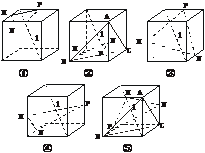
1.下列五个正方体图形中,l是正方体的一条对角线,点M、N、P分别是其所在棱的中点,能得出l⊥平面MNP的图形的序号是_____________.①④⑤.
7.已知向量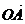 =(3,0,1),
=(3,0,1),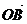 =(-1,1,2),
=(-1,1,2),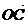 ⊥
⊥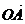 ,
,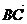 ∥
∥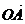 ,若
,若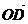 =
=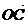 -
-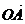 ,求向量
,求向量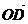 的坐标。(-
的坐标。(-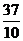 ,1,
,1,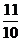 )
)
考查空间向量的概念及运算.要求空间向量的加法、减法和数乘、空间向量的坐标运算、空间向量的数量积的概念、性质.
6.若e1,e2,e3是三个不共面向量,试问向量a=3e1+2e2+e3,b=-e1+ e 2+3 e 3,c=2e 1-e 2-4 e 3是否共面,并说明理由。
解:由共面向量定理可知,关键是能否找到三个不全为零的实数x,y,z,
使得xa+yb+zc=0,即x(3 e1+2e2+e3)+y(-e1+ e 2+3 e 3)+z(2 e 1-e 2-4 e 3)=0,
即(3x-y+2z)e1+(2x+y-z)e2+(x+3y-4z)e3=0。由于e1,e2,e3不共面,
故得3x-y+2z=0,① 2x+y-z=0,② x+3y-4z=0。③
①+②求得z=-5x,代入③得y=-7x,取x=1,则y=-7,z=-5,于是a-7b-5c=0,
即a=7b+5c,所以a,b,c三向量共面。
5.已知 、
、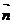 是空间两个单位向量,它们的夹角为60°,设向量
是空间两个单位向量,它们的夹角为60°,设向量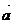 =2
=2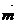 +
+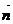 ,
,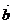 =-3
=-3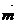 +2
+2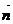 ,则向量
,则向量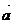 与
与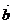 的夹角是_______.120°
的夹角是_______.120°
4.命题:
①若a与b共线,b与c共线,则a与c共线;
②向量a、b、c共面,则它们所在的直线也共面;
③若a与b共线,则存在唯一的实数λ,使b=λa;
④若A、B、C三点不共线,O是平面ABC外一点,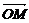 =
= 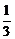
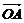 +
+ 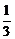
 +
+ 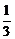
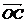 ,
,
则点M一定在平面ABC上,且在△ABC内部.
上述命题中的真命题是_____________.④
解:①中b为零向量时,a与c可以不共线,故①是假命题;②中a所在的直线其实不确定,故②是假命题;③中当a=0,而b≠0时,则找不到实数λ,使b=λa,故③是假命题;④中M是△ABC的重心,故M在平面ABC上且在△ABC内,故④是真命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com