
3.火星的质量和半径分别约为地球的和,地球表面的重力加速度为g,则火星表面的重力加速度约为 ( )
A.0.2g B.0.4g C.2.5g D.5g
解析:由万有引力公式,在地球表面有G=mg ①
在火星表面有G=mg火 ②
由①②得g火=·g=0.4g,故B正确.
答案:B
2.宇宙中两个星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则下列说法错误的是 ( )
A.双星相互间的万有引力减小
B.双星圆周运动的角速度增大
C.双星圆周运动的周期增大
D.双星圆周运动的半径增大
解析:距离增大万有引力减小,A正确;由m1r1ω2=m2r2ω2及r1+r2=r,得r1=,r2=,可知D正确.F=G=m1r1ω2=m2r2ω2,r增大F减小,r1增大,故ω减小,B错;由T=知C正确.
答案:B
1.(2009·广东高考)宇宙飞船在半径为R1的轨道上运行,变轨后的半径为R2,R1>R2,宇宙飞船绕地球做匀速圆周运动,则变轨后宇宙飞船的 ( )
A.线速度变小 B.角速度变小
C.周期变大 D.向心加速度变大
解析:根据G=m=mω2r=m=ma向得v= ,可知变轨后飞船的线速度变大,A错;角速度变大,B错;周期变小,C错;向心加速度变大,D正确.
答案:D
12.已知a>0,函数f(x)=-2asin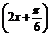 +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f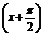 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间.
解 (1)∵x∈ ,∴2x+
,∴2x+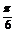 ∈
∈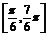 .
.
∴sin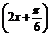 ∈
∈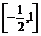 ,
,
∴-2asin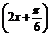 ∈[-2a,a].
∈[-2a,a].
∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,因此可得b=-5,3a+b=1,
因此a=2,b=-5.
(2)由(1)知a=2,b=-5,
∴f(x)=-4sin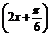 -1,
-1,
g(x)=f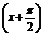 =-4sin
=-4sin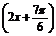 -1
-1
=4sin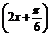 -1.
-1.
又由lg g(x)>0得g(x)>1,∴4sin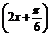 -1>1,
-1>1,
∴sin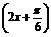 >
>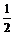 ,
,
∴2k +
+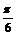 <2x+
<2x+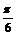 <2k
<2k +
+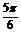 ,k∈Z.
,k∈Z.
由2k +
+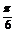 <2x+
<2x+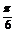 ≤2k
≤2k +
+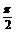 (k∈Z),得g(x)的单调增区间为:
(k∈Z),得g(x)的单调增区间为: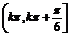 (k∈Z)
(k∈Z)
由2k +
+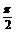 ≤2x+
≤2x+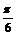 <2k
<2k +
+ ,
,
得g(x)的单调减区间为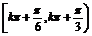 (k∈Z).
(k∈Z).
11.定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是 ,且当x∈
,且当x∈ 时,f(x)=sinx.
时,f(x)=sinx.
(1)求当x∈[- ,0]时,f(x)的解析式;
,0]时,f(x)的解析式;
(2)画出函数f(x)在[- ,
, ]上的函数简图;
]上的函数简图;
(3)求当f(x)≥ 时,x的取值范围.
时,x的取值范围.
解 (1)∵f(x)是偶函数,∴f(-x)=f(x).
而当x∈ 时,f(x)=sinx.
时,f(x)=sinx.
∴当x∈ 时,
时,
f(x)=f(-x)=sin(-x)=-sinx.
又当x∈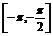 时,x+
时,x+ ∈
∈ ,
,
∵f(x)的周期为 ,
,
∴f(x)=f( +x)=sin(
+x)=sin( +x)=-sinx.
+x)=-sinx.
∴当x∈[- ,0]时,f(x)=-sinx.
,0]时,f(x)=-sinx.
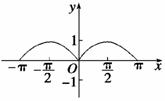 (2)如图:
(2)如图:
(3)由于f(x)的最小正周期为 ,
,
因此先在[- ,0]上来研究f(x)≥
,0]上来研究f(x)≥ ,
,
即-sinx≥ ,∴sinx≤-
,∴sinx≤- ,
,
∴- ≤x≤-
≤x≤-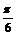 .
.
由周期性知,
当x∈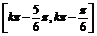 ,k∈Z时,f(x)≥
,k∈Z时,f(x)≥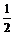 .
.
10.设a=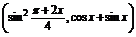 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数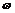 >0,若y=f(
>0,若y=f(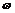 x)在区间
x)在区间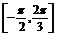 上是增函数,求
上是增函数,求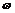 的取值范围;
的取值范围;
(3)设集合A=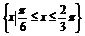 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A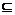 B,求实数m的取值范围.
B,求实数m的取值范围.
解 (1)f(x)=sin2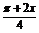 ·4sinx+(cosx+sinx)·(cosx-sinx)
·4sinx+(cosx+sinx)·(cosx-sinx)
=4sinx·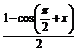 +cos2x
+cos2x
=2sinx(1+sinx)+1-2sin2x=2sinx+1,
∴f(x)=2sinx+1.
(2)∵f(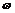 x)=2sin
x)=2sin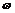 x+1,
x+1,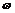 >0.
>0.
由2k -
-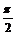 ≤
≤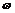 x≤2k
x≤2k +
+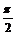 ,
,
得f(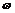 x)的增区间是
x)的增区间是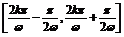 ,k∈Z.
,k∈Z.
∵f(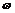 x)在
x)在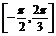 上是增函数,
上是增函数,
∴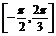
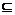
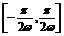 .
.
∴-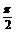 ≥
≥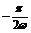 且
且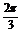 ≤
≤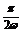 ,∴
,∴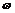 ∈
∈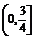 .
.
(3)由|f(x)-m|<2,得-2<f(x)-m<2,
即f(x)-2<m<f(x)+2.
∵A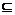 B,∴当
B,∴当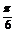 ≤x≤
≤x≤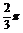 时,
时,
不等式f(x)-2<m<f(x)+2恒成立.
∴f(x)max-2<m<f(x)min+2,
∵f(x)max=f(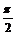 )=3,f(x)min=f(
)=3,f(x)min=f(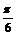 )=2,∴m∈(1,4).
)=2,∴m∈(1,4).
9.已知x∈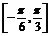 ,若方程mcosx-1=cosx+m有解,试求参数m的取值范围.
,若方程mcosx-1=cosx+m有解,试求参数m的取值范围.
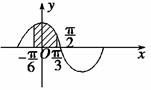 解 由mcosx-1=cosx+m得
解 由mcosx-1=cosx+m得
cosx=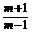 ,作出函数y=cosx的图象(如图所示),
,作出函数y=cosx的图象(如图所示),
由图象可得 ≤
≤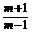 ≤1,解得m≤-3.
≤1,解得m≤-3.
8.(2009·东海高级中学高三调研)定义在R上的函数f(x):当sinx≤cosx时,f(x)=cosx;当sinx>cosx时,f(x)=sinx.给出以下结论:
①f(x)是周期函数
②f(x)的最小值为-1
③当且仅当x=2k (k∈Z)时,f(x)取最大值
(k∈Z)时,f(x)取最大值
④当且仅当2k -
-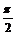 <x<(2k+1)
<x<(2k+1) (k∈Z)时,f(x)>0
(k∈Z)时,f(x)>0
⑤f(x)的图象上相邻最低点的距离是2 .
.
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
答案 ①④⑤
7.(2008·江苏,1)f(x)=cos(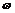 x-
x-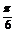 )最小正周期为
)最小正周期为 ,其中
,其中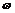 >0,则
>0,则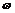 =
.
=
.
答案 10
6.给出下列命题:
①函数y=cos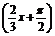 是奇函数;
是奇函数;
②存在实数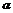 ,使得sin
,使得sin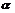 +cos
+cos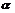 =
=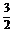 ;
;
③若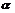 、
、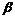 是第一象限角且
是第一象限角且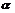 <
<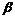 ,则tan
,则tan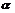 <tan
<tan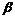 ;
;
④x=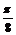 是函数y=sin
是函数y=sin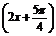 的一条对称轴方程;
的一条对称轴方程;
⑤函数y=sin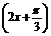 的图象关于点
的图象关于点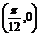 成中心对称图形.
成中心对称图形.
其中命题正确的是 (填序号).
答案 ①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com