1．(2010年福建普通高中质检)图甲示意“福建省1960-2005年平均台风降水量分布”，图乙示意“福建省台风降水年总量的变化”。读图，完成下列问题。

(1)据图并结合所学知识，分析福建省台风降水量的时空分布特点。

(2)说明福建沿海地区台风灾害严重的原因及其防御措施。

解析：第(1)题，依据甲图可以看出，福建省台风降水量自沿海向内陆逐渐减少；依据图乙可发现降水的年际变化大。第(2)题，对台风灾害的防御，可从工程措施、非工程措施等分析。

答案：(1)自沿海向内陆逐渐减少；主要集中在夏秋季节，年际变化大。

(2)台风频繁登陆区，狂风暴雨，易引发风暴潮、洪涝等；人口稠密，城镇众多，经济发达，造成严重损失。防御措施：加强对台风的监测和预警；植树造林；修建水利和护坡工程，加固堤防；制定救灾应急预案。

12．设f(x)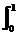＝|x²－a²|dx.

(1)当0≤a≤1与a＞1时，分别求f(a)；

(2)当a≥0时，求f(a)的最小值．

解：(1)0≤a≤1时，

f(a)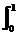＝|x²－a²|dx

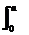＝(a²－x²)dx+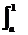(x²－a²)dx

＝(a²x－x³)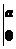+(－a²x)

＝a³－a³－0+0+－a²－+a³

＝a³－a²+.

当a＞1时，

f(a)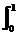＝(a²－x²)dx

＝(a²x－x³)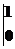

＝a²－.

∴f(a)＝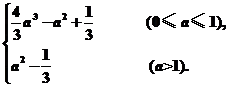

(2)当a＞1时，由于a²－在[1，+∞)上是增函数，故f(a)在[1，+∞)上的最小值是f(1)＝1－＝.

当a∈[0,1]时，f′(a)＝4a²－2a＝2a(2a－1)，

由f′(a)＞0知：a＞或a＜0，

故在[0，]上递减，在[，1]上递增．

因此在[0,1]上，f(a)的最小值为f()＝.

综上可知，f(x)在[0，+∞)上的最小值为.

11．(2010·温州模拟)若f(x)是一次函数，且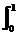f(x)dx＝5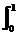，xf(x)dx＝，那么dx的值是________．

解析：∵f(x)是一次函数，∴设f(x)＝ax+b(a≠0)，由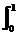(ax+b)dx＝5得(ax²+bx)＝a+b＝5，　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

由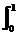xf(x)dx＝得 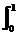(ax²+bx)dx＝，即

(ax³+bx²) ＝，∴a+b＝，　　　　　　　　　　　　　　　　　 ②

解①②得a＝4，b＝3，∴f(x)＝4x+3，

于是dx＝dx＝ (4+)dx

＝(4x+3lnx)＝8+3ln2－4＝4+3ln2.

答案：4+3ln2

10.(2010·烟台模拟)若y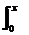＝(sint+costsint)dt，则y的最大值是　　　　　　　 (　)

A．1　 　　B．2 　　　　C．－ 　　　　D．0

解析：y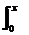＝(sint+costsint)dt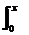＝(sint+sin2t)dt

＝(－cost－cos2t)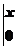＝－cosx－cos2x+

＝－cosx－(2cos²x－1)+＝－cos²x－cosx+

＝－(cosx+1)²+2≤2.

答案：B

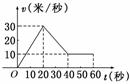
9．一辆汽车的速度-时间曲线如图所示，则该汽车在这一分钟内行驶的路程为_______米．

解析：据题意，v与t的函数关系式如下：

v＝v(t)＝

所以该汽车在这一分钟内所行驶的路程为

s＝＝++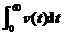

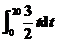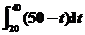＝t²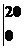+(50t－t²)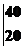+10t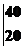

＝900米．

答案：900

8．若1 N的力能使弹簧伸长1 cm，现在要使弹簧伸长10 cm，则需要花费的功为(　)

A．0.05 J 　　B．0.5 J　　 C．0.25 J 　　　D．1 J

解析：设力F＝kx(k是比例系数)，当F＝1 N时，x＝0.01 m，可解得k＝100 N/m，则F＝100x，所以W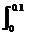＝100xdx＝50x²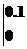＝0.5 J.

答案：B

7.一质点运动时速度与时间的关系为v(t)＝t²－t+2，质点作直线运动，则此物体在时间[1,2]内的位移为　　　　　　　　　　　　　 　　　　　　　　　　　　　　(　)

A.　　　B.　　　　 C.　 　　　　　D.

解析：s＝(t²－t+2)dt＝(t³－t²+2t)|＝.

答案：A

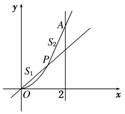
6．如图，设点P从原点沿曲线y＝x²向点A(2,4)移动，

记直线OP、曲线y＝x²及直线x＝2所围成的面积

分别记为S₁，S₂，若S₁＝S₂，则点P的坐标为________．

解析：设直线OP的方程为y＝kx, P点的坐标为(x，y)，

则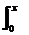(kx－x²)dx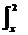＝(x²－kx)dx，

即(kx²－x³)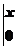＝(x³－kx²)，

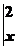解得kx²－x³＝－2k－(x³－kx²)，

解得k＝，即直线OP的方程为y＝x，所以点P的坐标为(，)．

答案：(，)

5．已知函数y＝x²与y＝kx(k＞0)的图象所围成的阴影部分

(如图所示)的面积为，则k＝________.

解析：直线方程与抛物线方程联立先求出积分区间为[0，k]，

再由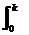(kx－x²)dx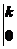＝(－)＝＝求得k＝2.

答案：2

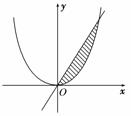
4．如图，函数y＝－x²+2x+1与y＝1相交形成一个闭合

图形(图中的阴影部分)，则该闭合图形的面积是　　 (　)

A．1　 　　B.　　　 C. 　　　　D．2

解析：函数y＝－x²+2x+1与y＝1的两个交点为(0,1)和(2,1)，所以闭合图形的面积等于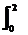(－x²+2x+1－1)dx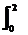＝(－x²+2x)dx＝.

答案：B