
6.I haven’t much b________ in his honesty.
5.Newspapers also carry financial reports,travel news and book and film r________.
4.Quality newspapers have home and international news,and sport and c________ events.
3.Popular newspapers are also known as tabloids.They have large h________.
2.Tokyo and New York are major ________(金融的)centres.
1.The ancient Romans ________(建立)colonies throughout Europe.
在复习过程 中抓住以下几点:
中抓住以下几点:
(1)坚持源于课本 、高于课本,以考纲为纲的原则。高考命题的依据是《高考说明》.并明确考点及对知识点与能力的要求作出了明确规定,其实质是精通课本,而本章考题大多数是课本的变式题,即源于课本,因此掌握双基、精通课本是关键;
、高于课本,以考纲为纲的原则。高考命题的依据是《高考说明》.并明确考点及对知识点与能力的要求作出了明确规定,其实质是精通课本,而本章考题大多数是课本的变式题,即源于课本,因此掌握双基、精通课本是关键;
(2)在注重解题方法、数学思想的应用的同时注意一些解题技巧,椭圆、双曲线、抛物线的定义揭示了各自存在的条件、性质及几何特征与圆锥曲线的焦点、焦半径、准线、离心率有关量的关系问题,若能用定义法,可避免繁 琐的推理与运算;
琐的推理与运算;
(3)焦半径公式:抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p>0):

题型1:椭圆的概念及标准方程
例1.求适合下列条件的椭圆的标准 方程:
方程:
(1)两个焦点的坐标分别是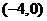 、
、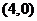 ,椭圆上一点
,椭圆上一点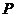 到两焦点距离的和等于
到两焦点距离的和等于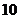 ;
;
(2)两个焦点的坐标分别是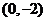 、
、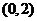 ,并且椭圆经过点
,并且椭圆经过点 ;
;
(3)焦点在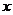 轴上,
轴上,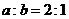 ,
,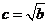 ;
;
(4)焦点在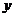 轴上,
轴上,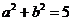 ,且过点
,且过点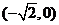 ;
;
(5)焦距为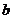 ,
,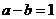 ;
;
(6)椭圆经过两点 ,
,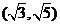 。
。
解析:(1)∵椭圆的焦点在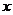 轴上,故设椭圆
轴上,故设椭圆 的标准方程为
的标准方程为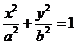 (
(
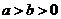 ),
),
∵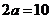 ,
,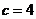 ,∴
,∴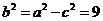 ,
,
所以,椭圆的标准方程为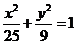 。
。
(2)∵椭圆焦点在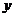 轴上,故设椭圆的标准方程为
轴上,故设椭圆的标准方程为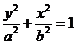 (
(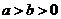 ),
),
由椭圆的定义知,
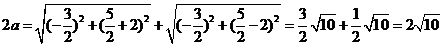 ,
,
∴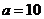 ,又∵
,又∵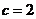 ,∴
,∴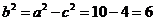 ,
,
所以,椭圆的标准方程为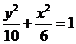 。
。
(3)∵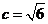 ,∴
,∴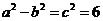 ,①
,①
又由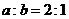 代入①得
代入①得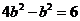 ,
,
∴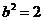 ,∴
,∴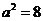 ,又∵焦点在
,又∵焦点在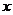 轴上,
轴上,
所以,椭圆的标准方程为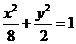 。
。
(4) 设椭圆方程为
设椭圆方程为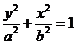 ,
,
∴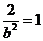 ,∴
,∴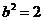 ,
,
又∵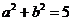 ,∴
,∴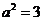 ,
,
所以,椭圆的标准方 程为
程为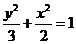 .
.
(5)∵焦距为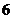 ,∴
,∴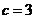 ,
,
∴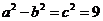 ,又∵
,又∵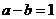 ,∴
,∴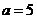 ,
,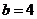 ,
,
所以,椭圆的标准方程为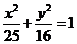 或
或 .
.
(6)设椭圆方程为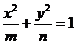 (
(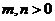 ),
),
由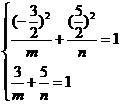 得
得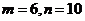 ,
,
所以,椭圆方程为 .
.
点评:求椭圆的方程首先清楚椭圆的定义,还要知道椭圆中一些几何要素与椭圆方程间的关系
例2.(1)(06山东)已知椭圆中心在原点,一个焦点为F(-2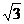 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
(2)(06天津理,8)椭圆的中心为点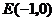 ,它的一个焦点为
,它的一个焦点为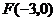 ,相应于焦点
,相应于焦点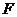 的准线方程为
的准线方程为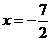 ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )
A.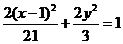 B.
B.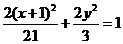
C.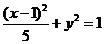 D.
D.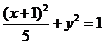
解析:(1)已知 为所求;
为所求;
(2)椭圆的中心为点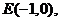 它的一个焦点为
它的一个焦点为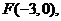
∴ 半焦距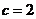 ,相应于焦点F的准线方程为
,相应于焦点F的准线方程为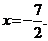
∴ 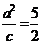 ,
,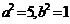 ,则这个椭圆的方程是
,则这个椭圆的方程是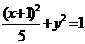 ,选D。
,选D。
点评:求椭圆方程的题目属于中低档题目,掌握好基础知识就可以。
题型2:椭圆的性质
例3.(1)(06山东理,7)在给定椭圆中,过焦点且垂直于长轴的弦长为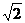 ,焦点到相应准线的距离为1,则该椭圆的离心率为( )
,焦点到相应准线的距离为1,则该椭圆的离心率为( )
(A)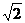 (B)
(B)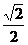 (C)
(C) 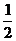 (D)
(D)
(2)(2009全国卷Ⅰ理)设双曲线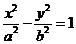 (a>0,b>0)的渐近线与抛物线y=x2
+1相切,则该双曲线的离心率等于( )
(a>0,b>0)的渐近线与抛物线y=x2
+1相切,则该双曲线的离心率等于( )
A.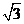 B.2
C.
B.2
C. D.
D.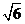
[解析]设切点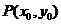 ,则切线的斜率为
,则切线的斜率为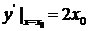 .
.
由题意有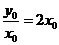 又
又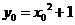
解得: 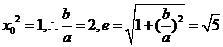 .
.
[答案]C
点评:本题重点考查了椭圆和双曲线的基本性质。
例4.(1)((2009全国卷Ⅰ理)已知椭圆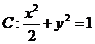 的右焦点为
的右焦点为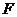 ,右准线为
,右准线为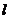 ,点
,点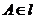 ,线段
,线段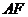 交
交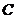 于点
于点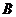 ,若
,若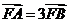 ,则
,则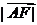 =( )
=( )
A. 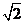 B.
2
C.
B.
2
C.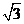 D. 3
D. 3 
[解析]过点B作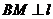 于M,并设右准线
于M,并设右准线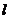 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意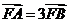 ,故
,故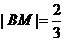 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得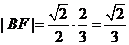
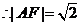 .故选A
.故选A
[答案]A
(2)(2009浙江理)过双曲线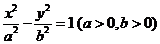 的右顶点
的右顶点 作斜率为
作斜率为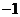 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为 .若
.若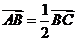 ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )
A.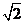 B.
B.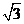 C.
C. D.
D.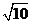
[解析]对于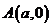 ,则直线方程为
,则直线方程为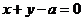 ,直线与两渐近线的交点为B,C,
,直线与两渐近线的交点为B,C,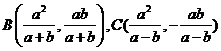 则有
则有
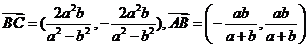 ,因
,因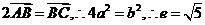 .
.
[答案]C
题型3:双曲线的方程
例5.(1)已知焦点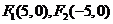 ,双曲线上的一点
,双曲线上的一点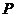 到
到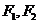 的距离差的绝对值等于
的距离差的绝对值等于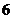 ,求双曲线的标准方程;
,求双曲线的标准方程;
(2)求与椭圆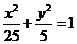 共焦点且过点
共焦点且过点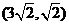 的双曲线的方程;
的双曲线的方程;
(3)已知双曲线的焦点在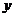 轴上,并且双曲线上两点
轴上,并且双曲线上两点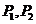 坐标分别为
坐标分别为 ,求双曲线的标准方程。
,求双曲线的标准方程。
解析:(1)因为双曲线的焦点在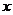 轴上,所以设它的标准方程为
轴上,所以设它的标准方程为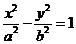
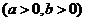 ,
,
∵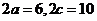 ,∴
,∴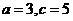 ,∴
,∴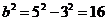 。
。
所以所求双曲线的方程为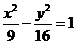 ;
;
(2)椭圆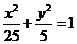 的焦点为
的焦点为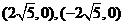 ,可以设双曲线的方程为
,可以设双曲线的方程为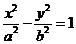 ,则
,则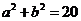 。
。
又∵过点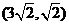 ,∴
,∴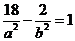 。
。
综上得, ,所以
,所以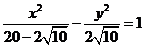 。
。
点评:双曲线的定义;方程确定焦点的方法;基本量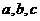 之间的关系。
之间的关系。
(3)因为双曲线的焦点在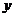 轴上,所以设所求双曲线的标准方程为
轴上,所以设所求双曲线的标准方程为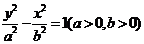 ①;
①;
∵点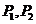 在双曲线上,∴点
在双曲线上,∴点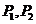 的坐标适合方程①。
的坐标适合方程①。
将 分别代入方程①中,得方程组:
分别代入方程①中,得方程组: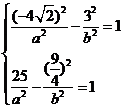
将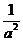 和
和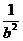 看着整体,解得
看着整体,解得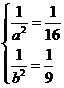 ,
,
∴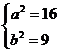 即双曲线的标准方程为
即双曲线的标准方程为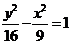 。
。
点评:本题只要解得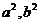 即可得到双曲线的方程,没有必要求出
即可得到双曲线的方程,没有必要求出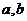 的值;在求解的过程中也可以用换元思想,可能会看的更清楚
的值;在求解的过程中也可以用换元思想,可能会看的更清楚
例6.已知双曲线中心在原点,一个顶点的坐标为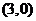 ,且焦距与虚轴长之比为
,且焦距与虚轴长之比为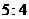 ,则双曲线的标准方程是____________________.
,则双曲线的标准方程是____________________.
解析:双曲线中心在原点,一个顶点的坐标为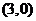 ,则焦点在x轴上,且a=3,焦距与虚轴长之比为
,则焦点在x轴上,且a=3,焦距与虚轴长之比为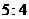 ,即
,即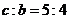 ,解得
,解得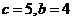 ,则双曲线的标准方程是
,则双曲线的标准方程是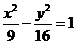 ;
;
点评:本题主要考查双曲线的基础知识以及综合运用知识解决问题的能力。充分挖掘双曲线几何性质,数形结合,更为直观简捷
题型4:双曲线的性质
例7.(1)(2009安徽卷理)下列曲线中离心率为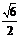 的是
的是
A.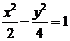 B.
B.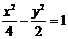 C.
C.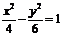 D.
D.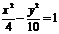
[解析]由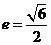 得
得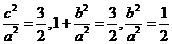 ,选B.
,选B.
[答案]B
(2)(2009江西卷文)设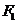 和
和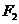 为双曲线
为双曲线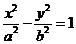 (
(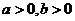 )的两个焦点, 若
)的两个焦点, 若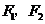 ,
,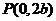 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为
A.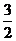 B.
B.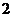 C.
C.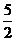 D.3
D.3
[解析]由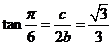 有
有 ,则
,则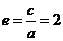 ,故选B.
,故选B.
[答案]B
(3)(2009天津卷文)设双曲线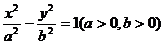 的虚轴长为2,焦距为
的虚轴长为2,焦距为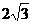 ,则双曲线的渐近线方程为(
)
,则双曲线的渐近线方程为(
)
A.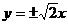 B .
B .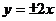 C .
C .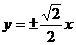 D.
D.
[解析]由已知得到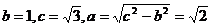 ,因为双曲线的焦点在x轴上,故渐近线方程为
,因为双曲线的焦点在x轴上,故渐近线方程为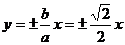
[答案]C
[考点定位]本试题主要考查了双曲线的几何性质和运用。考察了同学们的运算能力和推理能力。
例8.(1)(2009湖北卷理)已知双曲线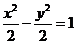 的准线过椭圆
的准线过椭圆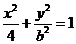 的焦点,则直线
的焦点,则直线 与椭圆至多有一个交点的充要条件是( )
与椭圆至多有一个交点的充要条件是( )
A. 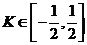
 B.
B. 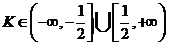
C. 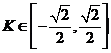 D.
D. 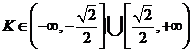
[解析]易得准线方程是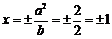
所以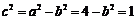 即
即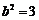 所以方程是
所以方程是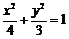
联立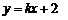 可得
可得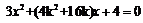 由
由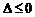 可解得A.
可解得A.
[答案]A
(2)(2009四川卷文、理)已知双曲线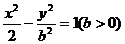 的左、右焦点分别是
的左、右焦点分别是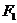 、
、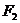 ,其一条渐近线方程为
,其一条渐近线方程为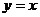 ,点
,点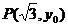 在双曲线上.则
在双曲线上.则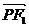 ·
·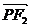 =( )
=( )
 A. -12
B. -2
C. 0
D. 4
A. -12
B. -2
C. 0
D. 4
[解析]由渐近线方程为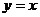 知双曲线是等轴双曲线,∴双曲线方程是
知双曲线是等轴双曲线,∴双曲线方程是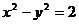 ,于是两焦点坐标分别是(-2,0)和(2,0),且
,于是两焦点坐标分别是(-2,0)和(2,0),且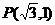 或
或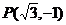 .不妨去
.不妨去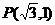 ,则
,则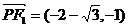 ,
,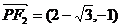 .
.
∴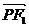 ·
·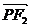 =
=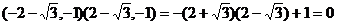
[答案]C
(3)(2009全国卷Ⅱ理)已知双曲线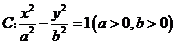 的右焦点为
的右焦点为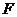 ,过
,过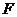 且斜率为
且斜率为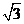 的直线交
的直线交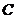 于
于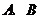 两点,若
两点,若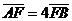 ,则
,则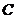 的离心率为 ( A.
的离心率为 ( A.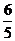 B.
B. 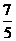 C.
C.
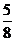 D.
D.
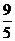
[解析]设双曲线 的右准线为
的右准线为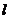 ,过
,过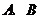 分 别作
分 别作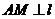 于
于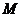 ,
,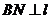 于
于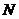 ,
, 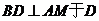 ,由直线AB的斜率为
,由直线AB的斜率为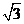 ,知直线AB的倾斜角
,知直线AB的倾斜角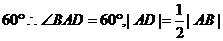 ,
,
由双曲线的第二定义有
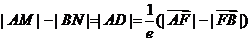
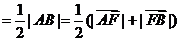 .
.
又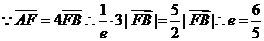 .
.
[答案]A
题型5:抛物线方程
例9.(1))焦点到准线的距离是2;
(2)已知抛物线的焦点坐标是F(0,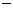 2),求它的标准方程
2),求它的标准方程
解析:(1)y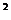 =4x,y
=4x,y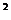 =
=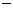 4x,x
4x,x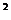 =4y,x
=4y,x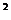 =
=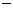 4y;
4y;
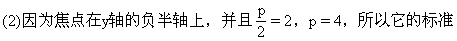
方程是x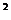 =
=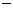 8y。
8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
题型6:抛物线的性质
例10.(1)若抛物线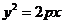 的焦点与椭圆
的焦点与椭圆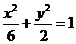 的右焦点重合,则
的右焦点重合,则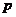 的值为( )
的值为( )
A.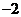 B.
B.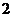 C.
C.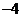 D.
D.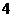
(2)抛物线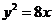 的准线方程是( )
的准线方程是( )
(A)  (B)
(B) 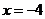 (C)
(C) 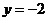 (D)
(D)
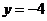
(3)(2009湖南卷文)抛物线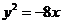 的焦点坐标是(
)
的焦点坐标是(
)
A.(2,0) B.(- 2,0) C.(4,0)
D.(- 4,0)
B.(- 2,0) C.(4,0)
D.(- 4,0)
解析:(1)椭圆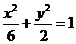 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线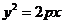 的焦点为(2,0),则
的焦点为(2,0),则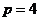 ,故选D;
,故选D;
(2)2p=8,p=4,故准线方程为x=-2,选A;
(3)[解析]由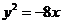 ,易知焦点坐标是
,易知焦点坐标是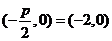 ,故选B.
,故选B.
[答案]B
点评:考察抛物线几何要素如焦点坐标、准线方程的题目根据定义直接计算机即可。
例11.(1)(全国卷I)抛物线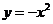 上的点到直线
上的点到直线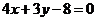 距离的最小值是( )
距离的最小值是( )
A.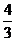 B.
B.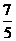 C.
C.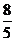 D.
D.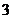
(2)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。
(3)对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则 a的取值范围是( )
a的取值范围是( )
A.(-∞,0) B.(-∞,2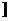 C.[0,2] D.(0,2)
C.[0,2] D.(0,2)
能使这抛物线方程为y2=10x的条件是 .(要求填写合适条件的序号)
解析:(1)设抛物线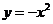 上一点为(m,-m2),该点到直线
上一点为(m,-m2),该点到直线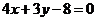 的距离为
的距离为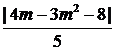 ,当m=
,当m= 时,取得最小值为
时,取得最小值为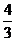 ,选A;
,选A;
(2)答案:②,⑤
解析:从抛物线方程易得②,分别按条件③、④、⑤计算求抛物线方程,从而确定⑤。
(3)答案:B
解析:设点Q的坐标为(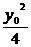 ,y0),
,y0),
由 |PQ|≥|a|,得y02+(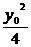 -a)2≥a2.
-a)2≥a2.
整理,得:y02(y02+16-8a)≥0,
∵y02≥0,∴y02+16-8a≥0.
即a≤2+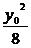 恒成立.而2+
恒成立.而2+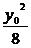 的最小值为2.
的最小值为2.
∴a≤2.选B。
点评:抛物线问题多考察一些距离、最值及范围问题。
3.抛物线
(1)抛物线的概念
平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上)。定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
方程 叫做抛物线的标准方程。
叫做抛物线的标准方程。
注意:它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是F(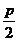 ,0),它
,0),它 的准线方程是
的准线方程是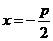 ;
;
(2)抛物线的性质
一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式: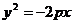 ,
,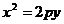 ,
, .这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下表:
.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下表:
|
标准方程 |
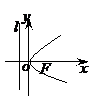 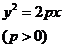 |
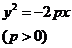 [来源:ZXXK] [来源:ZXXK] |
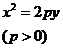 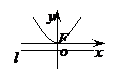 |
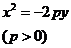 |
|
图形 |
|
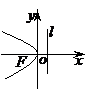 |
|
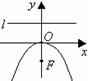 |
|
焦点坐标 |
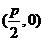 |
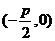 |
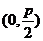 |
 |
|
准线方程 |
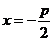 |
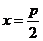 |
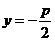 |
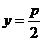 |
|
范围 |
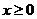 |
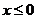 |
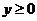 |
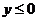 |
|
对称性 |
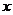 轴 轴 |
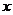 轴 轴 |
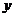 轴 轴 |
 轴 轴 |
|
顶点 |
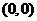 |
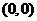 |
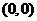 |
 |
|
离心率 |
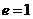 |
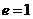 [来源:学#科#网] [来源:学#科#网] |
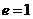 |
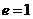 |
说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径;(2)抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,没有渐近线;(3)注意强调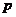 的几何意义:是焦点到准线的距离。
的几何意义:是焦点到准线的距离。
2.双曲线
(1)双曲线的概念
平面上与两点距离的差的绝对值为非零常数的动点轨迹是双曲线(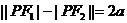 )。
)。
注意:①(*)式中是差的绝对值,在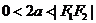 条件下;
条件下;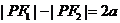 时为双曲线的一支(含
时为双曲线的一支(含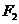 的一支);
的一支);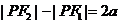 时为双曲线的另一支(含
时为双曲线的另一支(含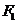 的一支);②当
的一支);②当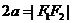 时,
时,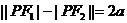 表示两条射线;③当
表示两条射线;③当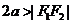 时,
时,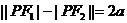 不表示任何图形;④两定点
不表示任何图形;④两定点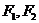 叫做双曲线的焦点,
叫做双曲线的焦点,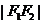 叫做焦距。
叫做焦距。
椭圆和双曲线比较:
|
|
椭
圆 |
双
曲 线 |
||
|
定义 |
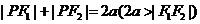 |
 |
||
|
方程 |
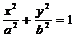 |
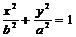 |
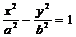 |
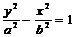 |
|
焦点 |
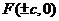 |
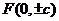 |
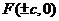 |
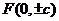 |
|
注意:如何有方程确定焦点的位置! |
(2)双曲线的性质
①范围:从标准方程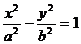 ,看出曲线在坐标系中的范围:双曲线在两条直线
,看出曲线在坐标系中的范围:双曲线在两条直线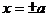 的外侧。即
的外侧。即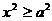 ,
, 即双曲线在两条直线
即双曲线在两条直线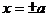 的外侧。
的外侧。
②对称性:双曲线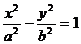 关于每个坐标轴和原点都是对称的,这时,坐标轴是双曲线的对称轴,原点是双曲线
关于每个坐标轴和原点都是对称的,这时,坐标轴是双曲线的对称轴,原点是双曲线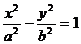 的对称中心,双曲线的对称中心叫做双曲线的中心。
的对称中心,双曲线的对称中心叫做双曲线的中心。
③顶点:双曲线和对称轴的交点叫做双曲线的顶点。在双曲线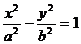 的方程里,对称轴是
的方程里,对称轴是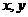 轴,所以令
轴,所以令 得
得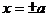 ,因此双曲线和
,因此双曲线和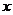 轴有两个交点
轴有两个交点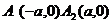 ,他们是双曲线
,他们是双曲线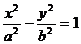 的顶点。
的顶点。
令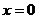 ,没有实根,因此双曲线和y轴没有交点。
,没有实根,因此双曲线和y轴没有交点。
1)注意:双曲线的顶点只有两个,这是与椭圆不同的(椭圆有四个顶点),双曲线的顶点分别是实轴的两个端点。
2)实轴:线段 叫做双曲线的实轴,它的长等于
叫做双曲线的实轴,它的长等于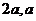 叫做双曲线的实半轴长。虚轴:线段
叫做双曲线的实半轴长。虚轴:线段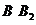 叫做双曲线的虚轴,它的长等于
叫做双曲线的虚轴,它的长等于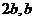 叫做双曲线的虚半轴长
叫做双曲线的虚半轴长
④渐近线:注意到开课之初所画的矩形,矩形确定了两条对角线,这两条直线即称为双曲线的渐近线。从图上看,双曲线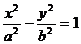 的各支向外延伸时,与这两条直线逐渐接近。
的各支向外延伸时,与这两条直线逐渐接近。
⑤等轴双曲线:
1)定义:实轴和虚轴等长的双曲线叫做等轴双曲线。定义式: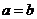 ;
;
2)等轴双曲线的性质:(1)渐近线方程为: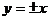 ;(2)渐近线互相垂直
;(2)渐近线互相垂直
注意以上几个性质与定义式彼此等价。亦即若题目中出现上述其一,即可推知双曲线为等轴双曲线,同时其他几个亦成立。
3)注意到等轴双曲线的特征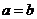 ,则等轴双曲线可以设为:
,则等轴双曲线可以设为: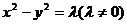 ,当
,当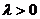 时交点在
时交点在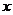 轴,当
轴,当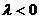 时焦点在
时焦点在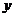 轴上
轴上
⑥注意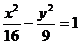 与
与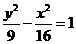 的区别:三个量
的区别:三个量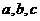 中
中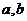 不同(互换)
不同(互换) 相同,还有焦点所在的坐标轴也变了。
相同,还有焦点所在的坐标轴也变了。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com