3.广州的一些商业街的建筑特色是许多商店一层楼的门前是贯通的前廊，如右图所

示，其目的是　　　　　　　　　　　　　　　　　　　　　 (　　 )

①增加街道宽度，便于人们的行走 　　　 ②体现建筑的层次美、节省建筑材料

③便于购物逛街的人们避雨　　　　　 　　 ④为购物逛街的人们遮挡阳光

A.①②　　　　　　　　　　 B.②③　　　　　　　 C.③④　　　　　　　 D.①④

答案　 C

2.由于气候的差异，北方和南方住宅窗户的朝向是不同的，最适宜的朝向是　　　　　　　 (　　 )

①北方避开西北方向　　　　　　　　　　　　　　 ②南方避开东南方向

③北方朝向西北方向　　　　　　　　　　　　　　 ④南方朝向东南方向

A.①②　　　　　　　　　　 B.①④　　　　　　　 C.②③　　　　　　　 D.③④

答案　 B

1.为了保证全年南侧楼房不遮挡北侧楼房的底层采光，楼房之间应相隔一定的距离。在楼高相同的情况下，楼房间距应越来越大的城市依次是　　　　　　　　　　　　　　　　　　 (　　 )

A.广州、珠海、上海、杭州　　　　　　　　　　　 B.海口、深圳、福州、南京

C.成都、重庆、西安、洛阳　　　　　　　　　　　 D.武汉、石家庄、包头、大连

答案　 B

2.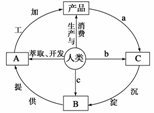读图，回答下列问题。

(1)写出图中字母、数字代表的内容：A.　　　　　　　　 B.　　　　　　 　　C.　　　　　　　　 a.　　　　　 b.　　　　　　　 c.　　　　　　　 。

(2)陆地自然资源包括　　　　　　　 资源、　　　　　　　　 资源、　　　　　　　　　 资源和生物资源。其中　　　　　　　　 资源属于非可再生资源。

(3)假若A地有丰富的森林资源，那么该地发展的社会第一级生产是　　　　　 ，在此基础上还可发展　　　

　　　　 业和　　　　　　 　业。

(4)从图中可知，人类主要是通过　　　　　 与环境发生关系的，在协调系统平衡中起　　　　　　 作用。

(5)假若A地煤、铁资源丰富，那么工业化时期以后，该地区的人口　　　　　 ，原因是　　　　　　　　　　　　 。

(6)陆地自然资源是人类文明和社会进步的物质基础，是人类进行生产活动的　　　　　　　　　 。

答案　 (1)自然资源　 陆地环境　 废弃物　 消费流通　 生产、生活排放　 改造控制

(2)矿产　 土地　 水　 矿产　 ?(3)林?业　 木材加工　 造纸　

(4)对自然资源的开发利用　 核心　 (5)增长过快　 工业化时期以后，煤铁资源成为发展生产的重要资源

(6)对象

命题视角　 自然资源特点及其分布、应用

[例](2007·北京文综)资源短缺和市场有限往往制约着一个国家的发展。历史上，许多国家为了获取资源、争夺市场采用了非和平的手段。我国政府明确指出，中国坚持走和平发展道路。完成下列问题。

以一种陆地资源为例，说明其特点和分布规律。

答案　 (1)举例：矿产、土地、水、生物资源(举出任意一种即可)

(2)特点和分布：①数量有限，利用潜力无限；②各种资源相互影响；③分布不均；④土地、水、生物资源分布一般具有地带性，矿产资源的分布受地质条件制约。

子　 变式演练

(2008·上海地理)当前，水资源紧缺已成为许多国家与地区经济发展的严重障碍，人们正在采取多种措施摆脱这一困境。

(1)通常所说的水资源，是指目前人类可以大量利用的　　　　　　　　　　　　　　　　　　　 (　　 )

A.冰川水、河水、湖泊水　　　　　　　　　　　 B.河水、淡水湖泊水、浅层地下水

C.冰川水、大气水、土壤水　　　　　　　　　　 D.大气水、淡水湖泊水、沼泽水

(2)根据自然条件与用水需求等因素判断，下列四组国家中，水资源都非常紧缺的一组是　　　　　　 (　　 )

A.埃及、新加坡　　　　　 B.巴西、阿根廷　 C.英国、以色列　　　 D.美国、墨西哥

(3)跨流域调水是解决地区水资源不足的措施之一。下列国家中，根据本国自然环境特点进行大规模“东水西调”的是 　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.俄罗斯　　　　　　 B.加拿大　　　　　　　　 C.中国　　　　　　　 D.澳大利亚

答案　 (1)B　 (2)A　 (3)D

住宅与气象、气候的关系是十分密切的。在我国的春联中常常可以看到“向阳门第春常在”这句话，意思是说一个住宅如果能经常得到阳光的照射，家人就会心情舒畅、精神愉快、健康长寿。住宅区房屋的建筑要充分利用当地气候的有利因素，避开不利因素，寻求适应于当地气候特点的建筑形式，利用建筑自身的调节能力创造怡人的小气候。据此回答1-3题。

1.读“某小区规划设计图”，回答下列问题。

(1)从光照条件分析，A、B、C三条街道规划合理的是　　　　　　　　　　　 ，理由是　　　　　　　　　 。

(2)居住区最好布局在小区　　　　　　　　　　　 方向。

(3)该小区的工业区应布局在小区的　　　　　　　　　 地区，理由是　　　　　　　　 　　　。

(4)若小区地处季风地区，夏季风与图中风向相反，则工业区应布局在小区的　　　　　　　　 地区。

答案　 (1)AC　 只有当街道与子午线成30°-60°夹角时，街道两侧所有建筑物才有较好的日照条件

(2)西北　 (3)东南　 使工业区位于常年风向的下风向，可减少工厂排放污染物对小区的影响

(4)东北或西南

考点二　 陆地资源

子　 强化专练

解法二　 设S_x＝Ax²+Bx(x∈N)

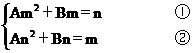
①－②，得A(m²－n²)+B(m－n)＝n－m

∵m≠n　 ∴ A(m+n)+B=－1

故A(m+n)²+B(m+n)＝－(m+n)

即S_m+n＝－(m+n)

说明　 a₁，d是等差数列的基本元素，通常是先求出基本元素，再

解的“整体化”思想，在解有关数列题目中值得借鉴．解法二中，由于是等差数列，由例22，故可设S_x=Ax²+Bx．(x∈N)

[例14]　 在项数为2n的等差数列中，各奇数项之和为75，各偶数项之和为90，末项与首项之差为27，则n之值是多少？

解　 ∵S_偶项－S_奇项=nd

∴nd=90－75=15

又由a_2n－a₁＝27，即(2n－1)d=27

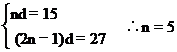
[例15]　 在等差数列{a_n}中，已知a₁＝25，S₉＝S₁₇，问数列前多少项和最大，并求出最大值．

解法一　 建立S_n关于n的函数，运用函数思想，求最大值．

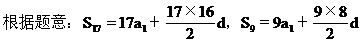
∵a₁=25，S₁₇＝S₉　 解得d＝－2

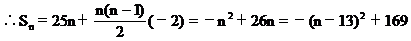
∴当n=13时，S_n最大，最大值S₁₃＝169

解法二　 因为a₁=25＞0，d＝－2＜0，所以数列{a_n}是递减等

∵a₁＝25，S₉＝S₁₇

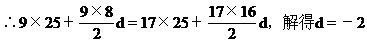
∴a_n=25+(n－1)(－2)=－2n+27

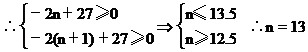
即前13项和最大，由等差数列的前n项和公式可求得S₁₃=169．

解法三　 利用S₉=S₁₇寻找相邻项的关系．

由题意S₉=S₁₇得a₁₀+a₁₁+a₁₂+…+a₁₇=0

而a₁₀+a₁₇=a₁₁+a₁₆=a₁₂+a₁₅=a₁₃+a₁₄

∴a₁₃+a₁₄＝0，a₁₃=－a₁₄　 ∴a₁₃≥0，a₁₄≤0

∴S₁₃=169最大．

解法四　 根据等差数列前n项和的函数图像，确定取最大值时的n．

∵{a_n}是等差数列

∴可设S_n＝An²+Bn

二次函数y=Ax²+Bx的图像过原点，如图3．2－1所示

∵S₉＝S₁₇，

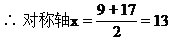
∴取n=13时，S₁₃＝169最大

3．要掌握对数列各项的同加、同减、同乘以某一个不等于零的数的变形方法，将其转化为常见的一些数列．

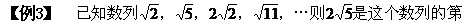
几项．

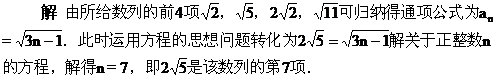
[例4]　 已知下面各数列{a_n}的前n项和S_n的公式，求数列的通项公式．

(1)S_n＝2n²－3n　　 (2)S_n＝n²+1

(3)S_n＝2ⁿ+3 　(4)S_n＝(－1)ⁿ⁺¹·n

解　 (1)当n=1时，a₁=S₁＝－1；

当n≥2时，a_n＝S_n－S_n-1=(2n²－3n)－[2(n－1)²－3(n－1)]＝4n－5，由于a₁也适合此等式，因此a_n=4n－5．

(2)当n＝1时，a₁＝S₁=1+1＝2；

当n≥2时，a_n＝S_n－S_n-1=n²+1－[(n－1)²+1]＝2n－1，由于a₁不适合于此等式，

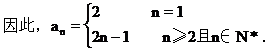
(3)当n＝1时，a₁=S₁＝2+3=5；

当n≥2时，a_n=S_n－S_n-1＝2ⁿ+3－(2^n-1+3)＝2^n-1，由于a₁不适合于此等式，

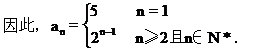
(4)当n＝1时，a₁＝S₁=(－1)²·1=1；

当n≥2时，a_n＝S_n－S_n-1=(－1)ⁿ⁺¹·n－(－1)ⁿ·(n－1)=(－1)ⁿ⁺¹(2n－1)，由于a₁也适可于此等式，因此a_n＝(－1)ⁿ⁺¹(2n－1)，n∈N*．

说明　 已知S_n求a_n时，要先分n＝1和n≥2两种情况分别进行计算，然后验证能否统一．

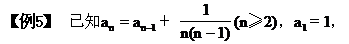
(1)写出数列的前5项；

(2)求a_n．

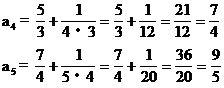
(2)由第(1)小题中前5项不难求出．

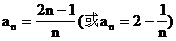
[例6]　 数列{a_n}中，a₁＝1，对所有的n≥2，都有a₁·a₂·a₃·…·a_n＝n²．

(1)求a₃+a₅；

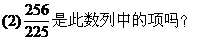
解　 由已知：a₁·a₂·a₃·…·a_n＝n²得

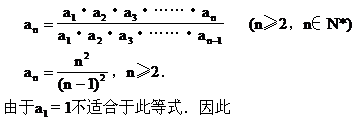
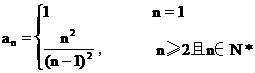
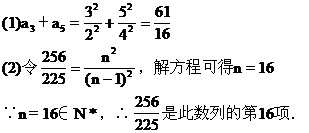
说明　 (1)“知和求差”、“知积求商”是数列中常用的基本方法．

(2)运用方程思想求n，若n∈N*，则n是此数列中的项，反之，则不是此数列中的项．

[例7]　 已知数a_n=(a²－1)(n³－2n)(a=≠±1)是递增数列，试确定a的取值范围．

解法一　 ∵数列{a_n}是递增数列，∴a_n+1＞a_n

a_n+1－a_n＝(a²－1)[(n+1)³－2(n+1)]－(a²－1)(n³－2n)

＝(a²－1)[(n+1)³－2(n+1)－n³+2n]

＝(a²－1)(3n²+3n－1)

∵(a²－1)(3n²+3n－1)＞0

又∵n∈N*，∴3n²+3n－1=3n(n+1)－1＞0

∴a²－1＞0，解得a＜－1或a＞1．

解法二　 ∵{a_n}是递增数列，∴a₁＜a₂即：

(a²－1)(1－2)＜(a²－1)(8－4)

化简得　 a²－1＞0

∴a＜－1或a＞1

说明　 本题从函数的观点出发，利用递增数列这一已知条件，将求取值范围的问题转化为解不等式的问题

2．对于常见的一些数列的通项公式(如：自然数列，a_n=n；自然数的平方数列，a_n＝n²；奇数数列，a_n＝2n－1；偶数数列，a_n=2n；

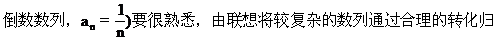
纳出数列的通项公式．

1．用归纳法写出数列的一个通项公式，体现了由特殊到一般的思维规律．对于项的结构比较复杂的数列，可将其分成几个部分分别考虑，然后将它们按运算规律结合起来．

2．

由eU₀=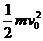得电子入射速度

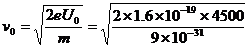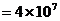m/sm/s　　 　

(1)加直流电压时，板间场强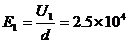V/m　　　 　

电子做直线运动时，由条件eE₁= ev₀B，

得应加磁场的磁感应强度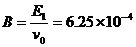T，　　 　

方向垂直纸面向里。　　　　 　

(2)加交流电压时，A、B两极间场强(V/m)

电子飞出板间时偏距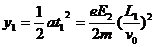　　 　

电子飞出板间时竖直速度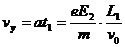　 　

从飞离板到达圆筒时偏距

在纸上记录落点的总偏距　

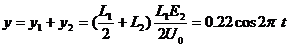(m) 　

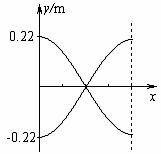
可见，在记录纸上的点以振幅0.20m，周期T=1s作简谐运动，

因圆筒每秒钟转2周，故在1s内，纸上图形如图所示。