
1.掌握机械能守恒定律,知道它的含义和适用条件,并能判断物体机械能守恒的条件。.
7.72 机械能守恒定律的应用
(第二课时)
Ⅰ 学习目标
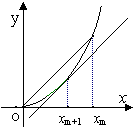
10. (2006浙江)已知函数f(x)=x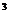 + x
+ x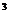 ,数列|x
,数列|x |(x
|(x >0)的第一项x
>0)的第一项x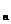 =1,以后各项按如下方式取定:曲线x=f(x)在
=1,以后各项按如下方式取定:曲线x=f(x)在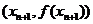 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x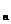 ,f (x
,f (x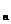 ))两点的直线平行(如图).
))两点的直线平行(如图).
求证:当n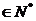 时,
时,
(Ⅰ)x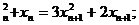
(Ⅱ)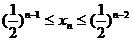
证明:(I)因为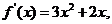
所以曲线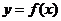 在
在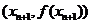 处的切线斜率
处的切线斜率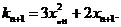
因为过 和
和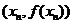 两点的直线斜率是
两点的直线斜率是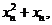
所以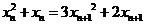 .
.
(II)因为函数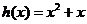 当
当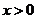 时单调递增,
时单调递增,
而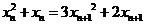
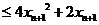
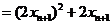 ,
,
所以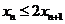 ,即
,即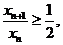
因此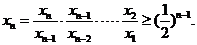
又因为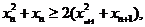 令
令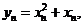 则
则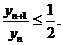
因为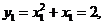 所以
所以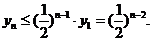
因此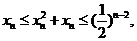 故
故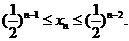
[探索题] 已知函数f(x)= f(x)的导函数是
f(x)的导函数是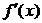
 对任意两个不相等的正数
对任意两个不相等的正数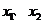 ,证明:当
,证明:当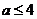 时,
时,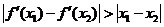

证法一:由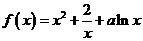 ,得
,得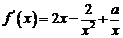
∴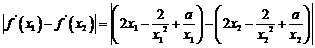
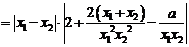
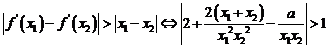
下面证明对任意两个不相等的正数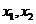 ,有
,有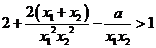 恒成立
恒成立
即证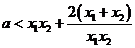 成立
成立
∵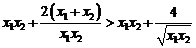
设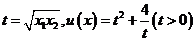 ,则
,则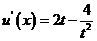
令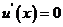 得
得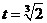 ,列表如下:
,列表如下:
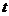 |
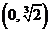 |
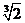 |
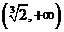 |
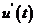 |
 |
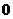 |
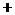 |
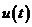 |
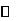 |
极小值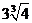 |
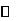 |
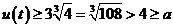 ∴
∴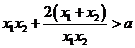
∴对任意两个不相等的正数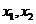 ,恒有
,恒有
证法二:由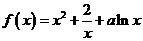 ,得
,得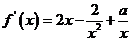
∴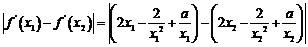
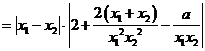
∵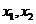 是两个不相等的正数
是两个不相等的正数
∴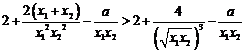
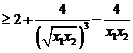
设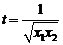 ,
,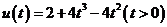
则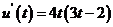 ,列表:
,列表:
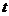 |
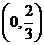 |
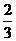 |
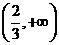 |
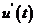 |
 |
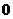 |
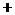 |
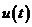 |
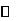 |
极小值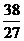 |
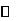 |
∴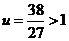 即
即 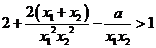
∴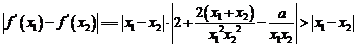
即对任意两个不相等的正数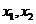 ,恒有
,恒有
9.(2006重庆)已知函数f(x)=(x2+bx+c)ex,其中b,c∈R为常数。
(Ⅰ)若b2>4(c-1),讨论函数f(x)的单调性;
(Ⅱ)若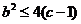 ,且
,且 ,试证:
,试证: 。
。
解(I)求导得f/(x)=[x2+(b+2)x+b+e]ex
∵b2>4(c-1)故方程f/(x)=0 即 x2+(b+2)x+b+e=0有两个实根
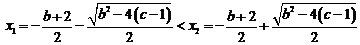
令f/(x)>0,解得x<x1,或x>x2.
又令f/(x)<0,解得x1<x<x2.
故当x∈(-∞,x1)时,f(x)是增函数,x∈(x2,+∞)时,f(x)也是函数,当x∈(x1,x2)时,f(x)是减函数。
(II)易知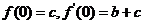
∴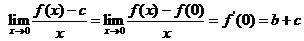
∴由已知条件得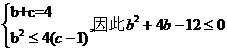
解得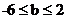
8.(2006江西)已知函数 在
在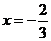 与
与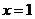 时都取得极值.
时都取得极值.
(1)求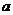 、
、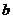 的值及函数f(x)的单调区间;
的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
解: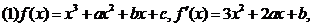
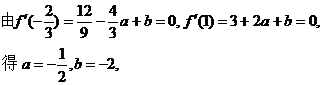
f/(x)=3x2-x-2=(3x-2)(x-1),函数f(x)的单调区间如下表:
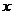 |
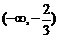 |
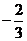 |
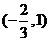 |
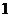 |
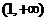 |
|
f/(x) |
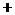 |
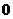 |
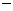 |
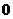 |
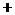 |
|
f(x) |
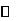 |
极大值 |
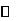 |
极小值 |
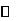 |
所以函数f(x)的递增区间为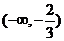 与
与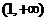 ;
;
递减区间为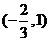 .
.

7. 已知x∈R,求证:ex≥x+1.
证明:设f(x)=ex-x-1,则f′(x)=ex-1.
∴当x=0时,f′(x)=0,f(x)=0.
当x>0时,f′(x)>0,∴f(x)在(0,+∞)上是增函数.∴f(x)>f(0)=0.
当x<0时,f′(x)<0,f(x)在(-∞,0)上是减函数,∴f(x)>f(0)=0.
∴对x∈R都有f(x)≥0.∴ex≥x+1.
5. 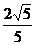 ; 6.设底面边长为x,则高为h=
; 6.设底面边长为x,则高为h= ,
,
∴S表=3× x+2×
x+2×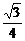 x2=
x2=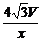 +
+ x2
x2
∴S′=-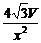 +
+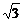 x
x 令S′=0,得x=
令S′=0,得x=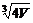 .答案:
.答案: 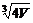
[解答题]
4. ,
,
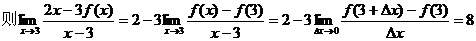
3.由f(-x)=f(x),求导得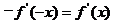 .
.
2.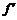 (x)=4x(x2-3x+5)在[1,2]上,
(x)=4x(x2-3x+5)在[1,2]上,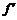 (x)>0,
(x)>0,
∴f(x)在[1,2]上单调递增.∴f(x)≥f(1)=7.
∴f(x)=0在[1,2]上无根.答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com