

6.设两个向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
解:由已知,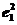 =|e1|2=4,
=|e1|2=4,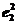 =|e2|2=1,
=|e2|2=1,
e1·e2=2×1×cos60°=1.
∴(2te1+7e2)·(e1+te2)=2t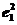 +(2t2+7)e1·e2+7t
+(2t2+7)e1·e2+7t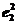
=2t2+15t+7.
由2t2+15t+7<0,得-7<t<-.
由2te1+7e2=λ(e1+te2)(λ<0),得,
∴.由于2te1+7e2与e1+te2的夹角为钝角,
故(2te1+7e2)·(e1+te2)<0且2te1+7e2≠λ(e1+te2)(λ<0),故t的取值范围是(-7,-)∪(-,-).
|
题组三 |
两向量的平行与垂直 |
5.在△ABC中,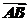 ·
·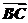 =3,△ABC的面积S∈[,],则
=3,△ABC的面积S∈[,],则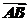 与
与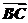 夹角的取值范围是
( )
夹角的取值范围是
( )
A.[,] B.[,] C.[,] D.[,]
解析:设〈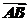 ·
·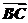 〉=θ,由
〉=θ,由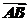 ·
·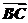 =|
=|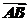 ||
||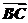 |cosθ=3,得|
|cosθ=3,得|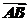 ||
||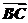 |=,
|=,
∴S=|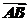 ||
||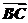 |sinθ=××sinθ=tanθ.
|sinθ=××sinθ=tanθ.
由≤tanθ≤,得≤tanθ≤1,
∴≤θ≤.
答案:B
4.(2009·全国卷Ⅰ)设非零向量a、b、c满足|a|=|b|=|c|,a+b=c,则〈a,b〉=( )
A.150° B.120° C.60° D.30°
解析:(a+b)2=c2,a·b=-,cos〈a,b〉==-,〈a,b〉=120°.
答案:B
3.(2009·福建高考)设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于 ( )
A.以a,b为两边的三角形的面积
B.以b,c为两边的三角形的面积
C.以a,b为邻边的平行四边形的面积
D.以b,c为邻边的平行四边形的面积
解析:设〈a,b〉=θ,θ∈(0,π),
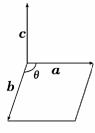 ∵〈a,c〉=,∴〈b,c〉=-θ,
∵〈a,c〉=,∴〈b,c〉=-θ,
以a,b为邻边的平行四边形面积为
|a||b|sinθ,而|b·c|=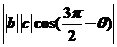
=|b||c|sinθ,
又|a|=|c|,∴|b·c|=|a||b|sinθ.
答案:C
|
题组二 |
两向量的夹角问题 |
2.(2009·广东高考)一质点受到平面上的三个力F1、F2、F3(单位:牛顿)的作用而处于平衡状态.已知F1、F2成60°角,且F1、F2的大小分别为2和4,则F3的
大小为 ( )
A.2 B.2 C.2 D.6
解析:由已知得F1+F2+F3=0,∴F3=-(F1+F2).
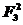 =
=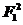 +
+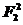 +2F1F2=
+2F1F2=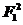 +
+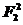 +2|F1||F2|cos60°=28.
+2|F1||F2|cos60°=28.
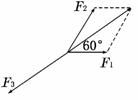 ∴|F3|=2.
∴|F3|=2.
答案:A
1.(2010·四平模拟)设a、b、c是单位向量,且a·b=0,则(a-c)·(b-c)的最小值为 ( )
A.-2 B.-2 C.-1 D.1-
解析:(a-c)·(b-c)=a·b-c·(a+b)+c2
=0-|c|·|a+b|·cos〈c,(a+b)〉+1
≥0-| c ||a+b|+1=-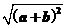 +1
+1
=-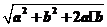 +1=-
+1=-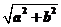 +1
+1
=-+1.
答案:D
本节课的内容相对比较简单,通过学生的自主学习学生要能够掌握核反应的概念以及核反应方程,两种 放射性同位素的异同点以及人工放射性同位素的一些应用,并能从物理学的原理上进行解释,还要了解核辐射的应用和防护。
放射性同位素的异同点以及人工放射性同位素的一些应用,并能从物理学的原理上进行解释,还要了解核辐射的应用和防护。
4.辐射与安全
学生通过看书与上网查找资料,了解放射性辐射的用处以及危害,知道只要控制好辐射量,我们就可以利用它的射线,知道身边的一些放射性物质,以及如何防护一些有害的放射性物质。
点评:这部分内容同样通过学生的自主性学习获得知识,同时也让学生知道核辐射并不可怕,只要控制好量并注意防护,培养学生学 科学,讲科学的意识。
科学,讲科学的意识。
3.放射性同位素的应用:
(1)利用射线:
射线测厚装置
烟雾报警器
放射治疗
培育新品种,延长保质期
学生要能说 出如何利用放射性物
出如何利用放射性物 质的射线的。对于书本的几种事例要能够讲清楚工作的原理。对学生上网查找的有关射线的应用也要能说出原理。
质的射线的。对于书本的几种事例要能够讲清楚工作的原理。对学生上网查找的有关射线的应用也要能说出原理。
点评:通过学生的自习与回答 问题,培养学生搜索信息,加工信息的能力,同时培养学生的表达能力,规范应用物理术语的能力。
问题,培养学生搜索信息,加工信息的能力,同时培养学生的表达能力,规范应用物理术语的能力。
(2)作为示踪原子
棉花对磷肥的吸收
甲状腺疾病的诊断
学生要说出如何将放射性物质作为示踪原子的原理。
2.人工放射性同位素
(1)放射性同位素:有些同位素具有放射性,叫做放射性同位素。放射性同位素有天然和人造两种,它们的化学性质相同。
(2)人工放射性同位素
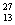 Al
Al 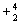 He
He  P
P 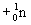
(3)人工放射性同位素的优点:放射强度容易控制;形状容易控制;半衰期短,废料容易处理。
(4)凡是用到射线时,都用人造放射性同位素
学生:从这部分开始主要为学生自习和上网查找资料,一方面要掌握书本的知识,另一方面要扩展自己的知识面,同时有问题的地方及时向老师提问,
点评:这一节大部分为陈述性的知识,教学难度不大,学生很容易掌握,如果让学生自习 并上网查相关资料
并上网查相关资料 ,他们一样可以掌握的很好,同时还能扩展他们的知识面,更能激发学生学习的热情。
,他们一样可以掌握的很好,同时还能扩展他们的知识面,更能激发学生学习的热情。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com