
8.气体分子运动的特点 (1)气体分子间有很大的空隙.气体分子之间的距离大约是分子直径的10倍.(2)气体分子之间的作用力十分微弱.在处理某些问题时,可以把气体分子看作没有相互作用的质点.(3)气体分子运动的速率很大,常温下大多数气体分子的速率都达到数百米每秒.离这个数值越远,分子数越少,表现出“中间多,两头少”的统计分布规律.
12.声波 (1)空气中的声波是纵波,传播速度为340m/s. (2)能够引起人耳感觉的声波频率范围是:20-20000Hz. (3)超声波:频率高于20000Hz的声波. ①超声波的重要性质有:波长短,不容易发生衍射,基本上能直线传播,因此可以使能量定向集中传播;穿透能力强. ②对超声波的利用:用声纳探测潜艇、鱼群,探察金属内部的缺陷;利用超声波碎石治疗胆结石、肾结石等;利用“B超”探察人体内病变. 13.多普勒效应:由于波源和观察者之间有相对运动使观察者感到频率发生变化的现象.其特点是:当波源与观察者有相对运动,两者相互接近时,观察者接收到的频率增大;两者相互远离时,观察者接收到的频率减小. 八、分子动理论、热和功、气体 1.分子动理论 (1)物质是由大量分子组成的 分子直径的数量级一般是10 -10 m. (2)分子永不停息地做无规则热运动. ①扩散现象:不同的物质互相接触时,可以彼此进入对方中去.温度越高,扩散越快.②布朗运动:在显微镜下看到的悬浮在液体(或气体)中微小颗粒的无规则运动,是液体分子对微小颗粒撞击作用的不平衡造成的,是液体分子永不停息地无规则运动的宏观反映.颗粒越小,布朗运动越明显;温度越高,布朗运动越明显. (3)分子间存在着相互作用力 分子间同时存在着引力和斥力,引力和斥力都随分子间距离增大而减小,但斥力的变化比引力的变化快,实际表现出来的是引力和斥力的合力. 2.物体的内能 (1)分子动能:做热运动的分子具有动能,在热现象的研究中,单个分子的动能是无研究意义的,重要的是分子热运动的平均动能.温度是物体分子热运动的平均动能的标志. (2)分子势能:分子间具有由它们的相对位置决定的势能,叫做分子势能.分子势能随着物体的体积变化而变化.分子间的作用表现为引力时,分子势能随着分子间的距离增大而增大.分子间的作用表现为斥力时,分子势能随着分子间距离增大而减小.对实际气体来说,体积增大,分子势能增加;体积缩小,分子势能减小. (3)物体的内能:物体里所有的分子的动能和势能的总和叫做物体的内能.任何物体都有内能,物体的内能跟物体的温度和体积有关. (4)物体的内能和机械能有着本质的区别.物体具有内能的同时可以具有机械能,也可以不具有机械能. 3.改变内能的两种方式 (1)做功:其本质是其他形式的能和内能之间的相互转化. (2)热传递:其本质是物体间内能的转移. (3)做功和热传递在改变物体的内能上是等效的,但有本质的区别. 4. ★能量转化和守恒定律 5★.热力学第一定律 (1)内容:物体内能的增量(ΔU)等于外界对物体做的功(W)和物体吸收的热量(Q)的总和. (2)表达式:W+Q=ΔU (3)符号法则:外界对物体做功,W取正值,物体对外界做功,W取负值;物体吸收热量,Q取正值,物体放出热量,Q取负值;物体内能增加,ΔU取正值,物体内能减少,ΔU取负值. 6.热力学第二定律(1)热传导的方向性 热传递的过程是有方向性的,热量会自发地从高温物体传给低温物体,而不会自发地从低温物体传给高温物体.(2)热力学第二定律的两种常见表述 ①不可能使热量由低温物体传递到高温物体,而不引起其他变化. ②不可能从单一热源吸收热量并把它全部用来做功,而不引起其他变化.(3)永动机不可能制成 ①第一类永动机不可能制成:不消耗任何能量,却可以源源不断地对外做功,这种机器被称为第一类永动机,这种永动机是不可能制造成的,它违背了能量守恒定律. ②第二类永动机不可能制成:没有冷凝器,只有单一热源,并从这个单一热源吸收的热量,可以全部用来做功,而不引起其他变化的热机叫做第二类永动机.第二类永动机不可能制成,它虽然不违背能量守恒定律,但违背了热力学第二定律. 7.气体的状态参量 (1)温度:宏观上表示物体的冷热程度,微观上是分子平均动能的标志.两种温标的换算关系:T=(t+273)K. 绝对零度为-273.15℃,它是低温的极限,只能接近不能达到. (2)气体的体积:气体的体积不是气体分子自身体积的总和,而是指大量气体分子所能达到的整个空间的体积.封闭在容器内的气体,其体积等于容器的容积. (3)气体的压强:气体作用在器壁单位面积上的压力.数值上等于单位时间内器壁单位面积上受到气体分子的总冲量. ①产生原因:大量气体分子无规则运动碰撞器壁,形成对器壁各处均匀的持续的压力. ②决定因素:一定气体的压强大小,微观上决定于分子的运动速率和分子密度;宏观上决定于气体的温度和体积. (4)对于一定质量的理想气体,PV/T=恒量
9.波的衍射 波在传播过程中偏离直线传播,绕过障碍物的现象.衍射现象总是存在的,只有明显与不明显的差异.波发生明显衍射现象的条件是:障碍物(或小孔)的尺寸比波的波长小或能够与波长差不多. 10.波的叠加 几列波相遇时,每列波能够保持各自的状态继续传播而不互相干扰,只是在重叠的区域里,任一质点的总位移等于各列波分别引起的位移的矢量和.两列波相遇前、相遇过程中、相遇后,各自的运动状态不发生任何变化,这是波的独立性原理. 11.波的干涉: 频率相同的两列波叠加,某些区域的振动加强,某些区域的振动减弱,并且振动加强和振动减弱的区域相互间隔的现象,叫波的干涉.产生干涉现象的条件:两列波的频率相同,振动情况稳定. [注意]①干涉时,振动加强区域或振动减弱区域的空间位置是不变的,加强区域中心质点的振幅等于两列波的振幅之和,减弱区域中心质点的振幅等于两列波的振幅之差. ②两列波在空间相遇发生干涉,两列波的波峰相遇点为加强点,波峰和波谷的相遇点是减弱的点,加强的点只是振幅大了,并非任一时刻的位移都大;减弱的点只是振幅小了,也并非任一时刻的位移都最小. 如图若S1、S2为振动方向同步的相干波源,当PS1-PS2=nλ时,振动加强;当PS1-PS2=(2n+1)λ/2时,振动减弱。
①在振幅很小的条件下,单摆的振动周期 跟振幅无关. ②单摆的振动周期跟摆球的质量无关,只与摆长L和当地的重力加速度g有关. ③摆长L是指悬点到摆球重心间的距离,在某些变形单摆中,摆长L应理解为等效摆长,重力加速度应理解为等效重力加速度(一般情况下,等效重力加速度g'等于摆球静止在平衡位置时摆线的张力与摆球质量的比值). 4.受迫振动 (1)受迫振动:振动系统在周期性驱动力作用下的振动叫受迫振动. (2)受迫振动的特点:受迫振动稳定时,系统振动的频率等于驱动力的频率,跟系统的固有频率无关. (3)共振:当驱动力的频率等于振动系统的固有频率时,振动物体的振幅最大,这种现象叫做共振. 共振的条件:驱动力的频率等于振动系统的固有频率. .5.机械波:机械振动在介质中的传播形成机械波.
(1)机械波产生的条件:①波源;②介质
(2)机械波的分类 ①横波:质点振动方向与波的传播方向垂直的波叫横波.横波有凸部(波峰)和凹部(波谷). ②纵波:质点振动方向与波的传播方向在同一直线上的波叫纵波.纵波有密部和疏部. [注意]气体、液体、固体都能传播纵波,但气体、液体不能传播横波.
(3)机械波的特点 ①机械波传播的是振动形式和能量.质点只在各自的平衡位置附近振动,并不随波迁移. ②介质中各质点的振动周期和频率都与波源的振动周期和频率相同.③离波源近的质点带动离波源远的 质点依次振动. 6.波长、波速和频率及其关系 (1)波长:两个相邻的且在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长.振动在一个周期里在介质中传播的距离等于一个波长.
(2)波速:波的传播速率.机械波的传播速率由介质决定,与波源无关.
(3)频率:波的频率始终等于波源的振动频率,与介质无关.
(4)三者关系:v=λf 7. ★波动图像:表示波的传播方向上,介质中的各个质点在同一时刻相对平衡位置的位移.当波源作简谐运动时,它在介质中形成简谐波,其波动图像为正弦或余弦曲线. (1)由波的图像可获取的信息 ①从图像可以直接读出振幅(注意单位).②从图像可以直接读出波长(注意单位). ③可求任一点在该时刻相对平衡位置的位移(包括大小和方向) ④在波速方向已知(或已知波源方位)时可确定各质点在该时刻的振动方向.⑤可以确定各质点振动的加速度方向(加速度总是指向平衡位置)
(2)波动图像与振动图像的比较:
|
|
振动图象 |
波动图象 |
|
研究对象 |
一个振动质点 |
沿波传播方向所有的质点 |
|
研究内容 |
一个质点的位移随时间变化规律 |
某时刻所有质点的空间分布规律 |
|
图象 |
|
|
|
物理意义 |
表示一质点在各时刻的位移 |
表示某时刻各质点的位移 |
|
图象变化 |
随时间推移图象延续,但已有形状不变 |
随时间推移,图象沿传播方向平移 |
|
一个完整曲线占横坐标距离 |
表示一个周期 |
表示一个波长 |
8.波动问题多解性 波的传播过程中时间上的周期性、空间上的周期性以及传播方向上的双向性是导致“波动问题多解性”的主要原因.若题目假设一定的条件,可使无限系列解转化为有限或惟一解
12.(文)已知向量m=(cos,cos),n=(cos,sin),且x∈[0,π],令函数f(x)=2a m·n+b.
(1)当a=1时,求f(x)的递增区间;
(2)当a<0时,f(x)的值域是[3,4],求a、b.
解:f(x)=2a m·n+b
=2a(cos2+sinx)+b
=2a(cosx+sinx+)+b
=a(sinx+cosx)+a+b
=asin(x+)+a+b.
(1)当a=1时,f(x)=sin(x+)+1+b.
令-+2kπ≤x+≤+2kπ,
得-π+2kπ≤x≤+2kπ(k∈Z),
又x∈[0,π],∴f(x)的递增区间为[0,].
(2)当a<0时,∵x∈[0,π],
∴x+∈[,],∴sin(x+)∈[-,1].
当sin(x+)=-时,f(x)=-a+a+b=b,
∴f(x)的最大值为b.
当sin(x+)=1时,f(x)=a+a+b=(1+)a+b.
∴f(x)的最小值为(1+)a+b.
∴解得a=1-,b=4.
(理)已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c.向量m=(a,4cosB),n=(cosA,b)满足m∥n.
(1)求sinA+sinB的取值范围;
(2)若实数x满足abx=a+b,试确定x的取值范围.
解:(1)因为m∥n,所以=,即ab=4cosAcosB.
因为△ABC的外接圆半径为1,由正弦定理,得
ab=4sinAsinB.
于是cosAcosB-sinAsinB=0,即cos(A+B)=0.
因为0<A+B<π.所以A+B=.故△ABC为直角三角形.
sinA+sinB=sinA+cosA=sin(A+),
因为<A+<,
所以<sin(A+)≤1,故1<sinA+sinB≤.
(2)x===.
设t=sinA+cosA(1<t≤),则2sinAcosA=t2-1,
x=,因为x′=<0,
故x=在(1,]上是单调递减函数.
所以≥.所以实数x的取值范围是[,+∞).
11.(2009·浙江高考)设向量a,b满足:|a|=3,|b|=4,a·b=0,以a,b,a-b的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为 ( )
A.3 B.4 C.5 D.6
解析:当圆与三角形两边都相交时,有4个交点,本题新构造的三角形是直角三角形,其内切圆半径恰好为1.故它与半径为1的圆最多有4个交点.
答案:B
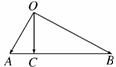
10.(2010·长郡模拟)已知|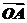 |=1,|
|=1,| |=,
|=,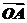 ·
· =0,
=0,
点C在∠AOB内,且∠AOC=30°,设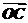 =m
=m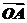 +n
+n
(m,n∈R),则等于 ( )
A. B.3 C. D.
解析:|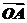 |=1,|
|=1,| |=,
|=,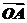 ·
· =0,
=0,
∴OA⊥OB,且∠OBC=30°,
又∵∠AOC=30°,∴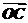
 ⊥
⊥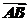 .
.
∴(m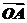 +n
+n )·(
)·( -
-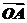 )=0,
)=0,
∴-m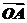 2+n
2+n 2=0,
2=0,
∴3n-m=0,
即m=3n,∴=3.
答案:B
9.已知平面向量a=(1,x),b=(2x+3,-x),x∈R.
(1)若a⊥b,求x的值;
(2)若a∥b,求|a-b|.
解:(1)若a⊥b,
则a·b=(1,x)·(2x+3,-x)
=1×(2x+3)+x(-x)=0.
整理得x2-2x-3=0,解得x=-1或x=3.
(2)若a∥b,则有1×(-x)-x(2x+3)=0,
即x(2x+4)=0,解得x=0或x=-2.
当x=0时,a=(1,0),b=(3,0),
∴|a-b|=|(1,0)-(3,0)|=|(-2,0)|
==2.
当x=-2时,a=(1,-2),b=(-1,2),
∴|a-b|=|(1,-2)-(-1,2)|=|(2,-4)|
==2.
|
题组四 |
平面向量数量积的综合应用 |
8.(2009·广东高考)若平面向量a,b满足|a+b|=1,a+b平行于x轴,b=(2,-1),则a=________.
解析:设a=(x,y),则a+b=(x+2,y-1)
由题意⇒
∴a=(-1,1)或a=(-3,1).
答案:(-1,1)或(-3,1)
7.已知向量a=(1,2),向量b=(x,-2),且a⊥(a-b),则实数x等于 ( )
A.-4 B.4 C.0 D.9
解析:∵a=(1,2),b=(x,-2),∴a-b=(1-x,4),
∵a⊥(a-b),∴a·(a-b)=0,∴1-x+8=0,∴x=9.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com