
23. (金华卷,本题10分)
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y = 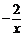 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
 (1)如图所示,若反比例函数解析式为y=
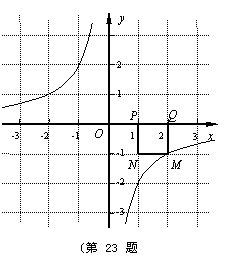
(1)如图所示,若反比例函数解析式为y= 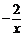 ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;
(温馨提示:作图时,别忘
了用黑色字迹的钢笔或签字
笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦ ▲ , 若点P的坐标为(m,0)时,则b﹦ ▲ ;
(3) 依据(2)的规律,如果点P的坐标为(6,0),请你求出点M1和点M的坐标.
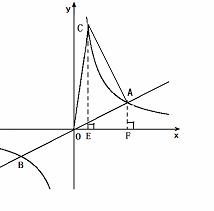
2.(2010年山东省济南市)如图,已知直线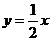 与双曲线
与双曲线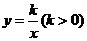 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线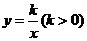 上一点C的纵坐标为8,求△AOC的面积;
上一点C的纵坐标为8,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线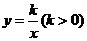 于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
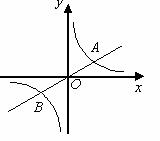
[关键词]反比例函数
[答案]
 (1)∵点A横坐标为4 ,
(1)∵点A横坐标为4 ,
∴当 x = 4时,y = 2
∴ 点A的坐标为(4,2 ) …………2’
∵点A是直线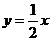 与双曲线
与双曲线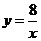 (k>0)的交点,
(k>0)的交点,
∴ k = 4×2 = 8 ………….3’
(2)解法一:
∵ 点C在双曲线 上,当y = 8时,x = 1
上,当y = 8时,x = 1
∴ 点C的坐标为(1,8)………..4’
过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMON
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4
S△AOC= S矩形ONDM-S△ONC-S△CDA-S△OAM
 = 32-4-9-4 = 15 ………..6’
= 32-4-9-4 = 15 ………..6’
解法二:
过点 C、A分别做 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点C在双曲线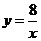 上,当y = 8时,x = 1。
上,当y = 8时,x = 1。
∴ 点C的坐标为(1,8)
∵ 点C、A都在双曲线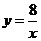 上,
上,
∴ S△COE = S△AOF = 4
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA
∵ S梯形CEFA = ×(2+8)×3 = 15,
×(2+8)×3 = 15,
∴ S△COA = 15
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
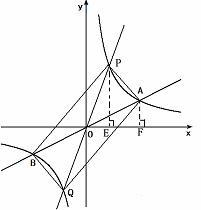 ∴ OP=OQ,OA=OB
∴ OP=OQ,OA=OB
∴ 四边形APBQ是平行四边形
∴ S△POA = 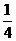 S平行四边形APBQ =
S平行四边形APBQ =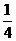 ×24 = 6
×24 = 6
设点P的横坐标为m(m > 0且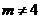 ),
),
得P(m,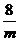 ) …………..7’
) …………..7’
过点P、A分别做 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4
若0<m<4,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6
∴ 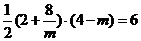
解得m= 2,m= - 8(舍去)
∴ P(2,4) ……………8’
若 m> 4,
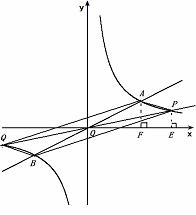 ∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6
∴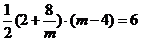 ,
,
解得m= 8,m =-2 (舍去)
∴ P(8,1)
∴ 点P的坐标是P(2,4)或P(8,1)………….9’
1. (2010年山东省济南市)若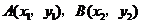 是双曲线
是双曲线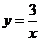 上的两点,且
上的两点,且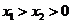 ,则
,则 {填“>”、“=”、“<”}.
{填“>”、“=”、“<”}.
[关键词]反比例函数
[答案]<
7.(2010年门头沟区)若反比例函数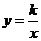 的图象经过点
的图象经过点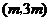 ,其中
,其中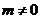 ,则此反比例函数的图象在
,则此反比例函数的图象在
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
[关键词]反比例函数图象
[答案]A
16.(2010年北京崇文区) 如图,点 是直线
是直线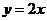 与曲线
与曲线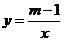 (
(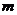 为常数
为常数 )一支的交点.过点
)一支的交点.过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为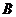 ,且
,且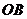 =2.求点
=2.求点 的坐标及
的坐标及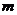 的值.
的值.
[关键词]一次函数与反比例函数图象交点坐标
 [答案]解:由题意,可知点
[答案]解:由题意,可知点 的横坐标是2,由点
的横坐标是2,由点 在正比例函数
在正比例函数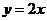 的图象上,
的图象上,
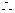 点
点 的坐标为
的坐标为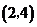 .
.
又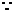 点
点 在反比例函数
在反比例函数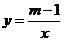 的图象上,
的图象上,
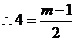 ,即
,即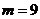 .
.
2、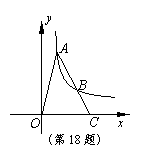 (2010盐城)如图,A、B是双曲线 上的点, A、B两点的横坐标
(2010盐城)如图,A、B是双曲线 上的点, A、B两点的横坐标
分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则
k= ▲ .
关键词:反比例的比例系数k与三角形面积
答案:4
1、(2010福建德化)如图,直线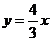 与双曲线
与双曲线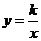 (
(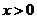 )交于点
)交于点 .将
.将
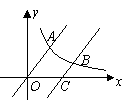 直线
直线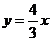 向下平移个6单位后,与双曲线
向下平移个6单位后,与双曲线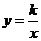 (
(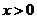 )交于点
)交于点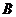 ,与
,与 轴交于点C,则C点的坐标为___________;若
轴交于点C,则C点的坐标为___________;若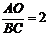 ,则
,则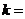
答案:(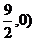 ,12
,12
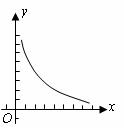
21.(2010年安徽省B卷)(本小题满分10分)已知图中的曲线是反比例函数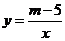 (
(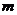 为常数)图象的一支.
为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数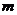 的取值范围是什么?
的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数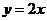 的图象在第一象内限的交点为
的图象在第一象内限的交点为 ,过
,过 点作
点作 轴的垂线,垂足为
轴的垂线,垂足为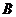 ,当
,当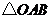 的面积为4时,求点
的面积为4时,求点 的坐标及反比例函数的解析式.
的坐标及反比例函数的解析式.
[关键词]反比例函数图像和解析式 正比例函数
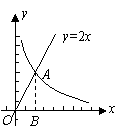 [答案](Ⅰ)这个反比例函数图象的另一支在第三象限.
[答案](Ⅰ)这个反比例函数图象的另一支在第三象限.
因为这个反比例函数的图象分布在第一、第三象限,
所以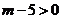 ,解得
,解得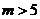 .
.
(Ⅱ)如图,由第一象限内的点 在正比例函数
在正比例函数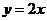 的图象上,
的图象上,
设点 的坐标为
的坐标为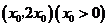 ,则点
,则点 的坐标为
的坐标为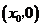 ,
,
 ,解得
,解得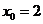 (负值舍去).
(负值舍去).
 点
点 的坐标为
的坐标为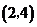 .
.
又 点
点 在反比例函数
在反比例函数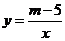 的图象上,
的图象上,
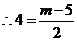 ,即
,即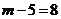 .
.
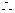 反比例函数的解析式为
反比例函数的解析式为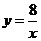 .
.
11、(2010年宁波)已知反比例函数 ,下列结论不正确的是( )
,下列结论不正确的是( )
A、图象经过点(1,1) B、图象在第一、三象限
C、当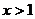 时,
时,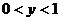 D、当
D、当 时,
时,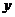 随着
随着 的增大而增大
的增大而增大
答案:D
(2010年安徽省B卷)3.若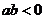 ,则正比例函数
,则正比例函数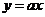 与反比例函数
与反比例函数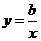 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
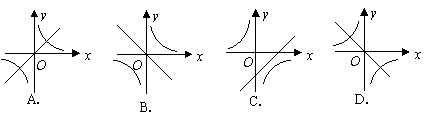
[关键词]正比例函数 反比例函数
[答案]B.
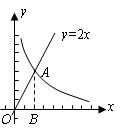
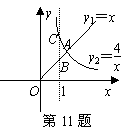
2.(2010年山东聊城)函数y1=x(x≥0),y2= (x>0)的图象如图所示,下列结论:
① 两函数图象的交点坐标为A(2,2);
② 当x>2时,y2>y1;
③ 直线x=1分别与两函数图象交于B、C两点,则线段BC的长为3;
④ 当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.
则其中正确的是()
A.只有①② B.只有①③ C.只有②④ D.只有①③④

[关键词]一次函数,反比例函数
[答案]D .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com