
1.作者简介:斯丹达尔(1783~1842),原名享利•贝尔,十九世纪法国批判现实主义文学的创始人。1783年1月23日出生于法国东部格勒诺布尔一个律师家庭,一生经历坎坷:从炮火连天的战场到呕心沥血的写作间;从拿破仑手下的军官到法国政府的驻外领事;从莫斯科到意大利海滨。丰富的经历带给他无尽的感受,也为他的个性和创作带来独特的魅力。他的主要作品有:《阿芒斯》、《红与黑》、《巴马修道院》《意大利遗事》及未完成的《吕西安.娄凡》。
他的文风简明、严谨,不带任何修饰,作品结构紧凑、层次分明,情节集中,善于捕捉人物的思想感情并塑造富有个性、充满矛盾的人物,对后代作家产生了深刻影响。高尔基曾经指出:“斯丹达尔是在资产阶级胜利之后,立即就开始敏锐而明确地表现它的特征的第一个文学家,他揭示出资产阶级社会内部腐化的不可避免和它的愚蠢的短见。” 斯丹达尔的作品具有鲜明的时代特征,丰富的社会内容。进步的文学观点和创作实践奠定了他在法国以至欧洲文学史上的重要地位。
4.交流评价人物形象。
文本导学
3.体会通过心理描写展现人物性格的写法。
2.了解小说《红与黑》的故事梗概及时代背景。
1.了解作者斯丹达尔。
3.红与黑
学习目标
1 选择题
选择题
(1)不等式6x2+5x<4的解集为( B )
A (-∞,-
(-∞,-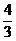 )∪(
)∪(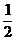 ,+∞) B
,+∞) B (-
(- 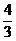 ,
,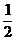 )
)
C (-
(- 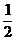 ,
, )
D
)
D (-∞,-
(-∞,-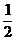 )∪(
)∪(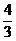 ,+∞)
,+∞)
(2)a>0,b>0,不等式a> >-b的解集为( C )
>-b的解集为( C )
A -
- <x<0或0<x<
<x<0或0<x<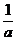 B
B -
- 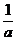 <x<
<x<
C x<-
x<- 或x>
或x>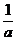 D
D -
- 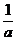 <x<0或0<x<
<x<0或0<x<
(3)不等式 (x-1)(x-2)2(x-3)<0的解集是(
B )
(x-1)(x-2)2(x-3)<0的解集是(
B )
A (-1,1)∪(2,3)
B
(-1,1)∪(2,3)
B (-∞,-1)∪(1,3)
(-∞,-1)∪(1,3)
C (-∞,-1)∪(2,3)
D
(-∞,-1)∪(2,3)
D R
R
(4)若a>0,且不等式ax2+bx+c<0无解,则左边的二次三项式的判别式(C )
A Δ<0 B
Δ<0 B Δ=0 C
Δ=0 C Δ≤0 D
Δ≤0 D Δ>0
Δ>0
(5)A={x|x2+(p+2)x+1=0,x∈R},且R*∩A=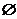 ,则有( B )
,则有( B )
A p>-2 B
p>-2 B p≥0 C
p≥0 C -4<p<0 D
-4<p<0 D p>-4
p>-4
(6)θ在第二象限,cosθ= ,sinθ=
,sinθ= ,则m满足( D )
,则m满足( D )
A m<-5或m>3 B
m<-5或m>3 B 3<m<9 C
3<m<9 C m=0或m=8 D
m=0或m=8 D m=8
m=8
(7)已知不等式loga(x2-x-2)>loga(-x2+2x+3)在x= 时成立,则不等式的解集为( B)
时成立,则不等式的解集为( B)
A {x|1<x<2}
B
{x|1<x<2}
B {x|2<x<
{x|2<x<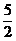 } C
} C {x|1<x<
{x|1<x<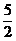 } D
} D {x|2<x<5}
{x|2<x<5}
(8)设0<b<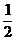 ,下列不等式恒成立的是( C )
,下列不等式恒成立的是( C )
A b3>b
b3>b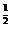 ?B
?B logb(1-b)>1 C
logb(1-b)>1 C cos(1+b)>cos(1-b) D
cos(1+b)>cos(1-b) D (1-b)n<bn,n∈N
(1-b)n<bn,n∈N
(9)若不等式x2-logax<0在(0,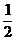 )内恒成立,则a满足( A )
)内恒成立,则a满足( A )
A
 ≤a<1 B
≤a<1 B
 <a<1 C
<a<1 C 0<a≤
0<a≤ D
D 0<a<
0<a<
(10)不等式 的解集是( A )
的解集是( A )
A [0,1] B
[0,1] B [0,+∞] C
[0,+∞] C (1,+∞) D
(1,+∞) D [-1,1]
[-1,1]
(11)不等式 的解集是( D )
的解集是( D )
A
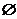 B
B (1,2)
C
(1,2)
C (2,+∞) D
(2,+∞) D (1,+∞)
(1,+∞)
(12)不等式(x-1) ≥0的解集是( B )
≥0的解集是( B )
A {x|x>1}
B
{x|x>1}
B {x|x≥1或x=-2} C
{x|x≥1或x=-2} C {x|x≥1} D
{x|x≥1} D {x|x≥-2且x≠1}
{x|x≥-2且x≠1}
(13)函数f(x)= 的定义域为A,函数g(x)=
的定义域为A,函数g(x)= 的定义域为B,则使A∩B=
的定义域为B,则使A∩B=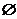 ,实数a的取值范围是( D )
,实数a的取值范围是( D )
A {a|-1<a<3} B
{a|-1<a<3} B {a|-2<a<4} C
{a|-2<a<4} C {a-2≤a≤4} D
{a-2≤a≤4} D {a|-1≤a≤3}
{a|-1≤a≤3}
(14)关于x的不等式 <2x+a(a>0)的解集为( B )
<2x+a(a>0)的解集为( B )
A (0,a) B
(0,a) B (0,a] C
(0,a] C (0,+∞)∪(-∞,-
(0,+∞)∪(-∞,- a)
D
a)
D
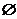
2 填空题
填空题
(1)不等式1≤|x-2|≤7的解集是
 答案:[-5,1]∪[3,9]
答案:[-5,1]∪[3,9]
(2)不等式 >a的解集是
>a的解集是  a=0时x>0;a>0时,0<x<
a=0时x>0;a>0时,0<x<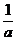 ;a<0时,x<
;a<0时,x<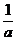 或x>0
或x>0
(3)不等式lg|x-4|<-1的解集是
 答案:{x|4<x<
答案:{x|4<x< 或
或 <x<4}
<x<4}
(4)不等式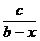 <a(a>0,b>0,c>0)的解集是
<a(a>0,b>0,c>0)的解集是  答案:{x|x<b或x>b-
答案:{x|x<b或x>b-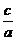 }
}
(5)若不等式 <0的解为-1<x<5,则a=
<0的解为-1<x<5,则a=  答案:4
答案:4
(6)不等式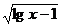 <3-lgx的解集是
<3-lgx的解集是  答案:10≤x<100
答案:10≤x<100
(7)函数f(x)=log2(x2-4),g(x)=2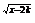 (k<-1),则f(x)g(x)的定义域为
(k<-1),则f(x)g(x)的定义域为  答案:[2k-2)∪(2,+∞)
答案:[2k-2)∪(2,+∞)
3 解下列不等式
解下列不等式
(1)(x+4)(x+5)2>(3x-2)(x+5)2;(2)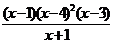 ≤0;(3)
≤0;(3)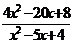 ≥3
≥3
解:(1)当x≠-5时,(x+5)2>0,两边同除以(x+5)2得x+4>3x-2,即x<3且x≠-5
∴x∈(-∞,-5)∪(-5,3)
(2)当x≠4时,原不等式 (x-1)(x-3)(x+1)≤0(x≠-1)
(x-1)(x-3)(x+1)≤0(x≠-1)  1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立
1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立
故原不等式的解集为{x|1≤x≤3或x<-1或x=4}
(3)原不等式可化为 -3≥0
-3≥0
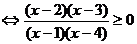 ∴x∈(-∞,1)∪[2,3]∪(4,+∞)
∴x∈(-∞,1)∪[2,3]∪(4,+∞)
4 设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围
设不等式(2x-1)>m(x2-1)对满足|m|≤2的一切实数m的值都成立,求x的取值范围
解:①若x2-1=0,即x=±1,且2x-1>0,即x>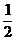 时,此时x=1,原不等式对|m|≤2恒成立;
时,此时x=1,原不等式对|m|≤2恒成立;
②若x2-1>0,要使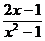 >m,对|m|≤2恒成立,只要
>m,对|m|≤2恒成立,只要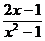 >2,即
>2,即
 得1<x<
得1<x<

③若x2-1<0时,要使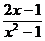 <m,对|m|≤2恒成立,只要
<m,对|m|≤2恒成立,只要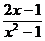 <-2,即
<-2,即
 得
得 <x<1
<x<1
综合①②③得,所求x的范围为 <x<
<x<

6.若方程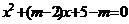 的两根都对于2,求实数m的范围
的两根都对于2,求实数m的范围 
5.当a在什么范围内方程: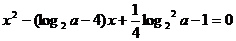 有两个不同的负根
有两个不同的负根 
4.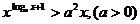

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com