10．已知圆C₁：x²+y²+2x+2y－8＝0与圆C₂：x²+y²－2x+10y－24＝0相交于A、B两点，

(1)求公共弦AB所在的直线方程；

(2)求圆心在直线y＝－x上，且经过A、B两点的圆的方程．

解：(1)⇒x－2y+4＝0.

(2)由(1)得x＝2y－4，代入x²+y²+2x+2y－8＝0中得：y²－2y＝0.

∴或，即A(－4,0)，B(0,2)，

又圆心在直线y＝－x上，设圆心为M(x，－x)，则|MA|＝|MB|，解得M(－3,3)，∴⊙M：(x+3)²+(y－3)²＝10.

9．(2009年高考江西卷)设直线系M：xcosθ+(y－2)sinθ＝1(0≤θ≤2π)，对于下列四个命题：

A．存在一个圆与所有直线相交

B．存在一个圆与所有直线不相交

C．存在一个圆与所有直线相切

D．M中的直线所能围成的正三角形面积都相等

其中真命题的代号是________(写出所有真命题的代号)．

解析：xcosθ+ysinθ－2sinθ－1＝0.则点(0,2)到其直线的距离为

d＝＝1.

∴说明此直线是圆心为(0,2)，半径为1的圆的切线．

圆心为(0,2)，半径大于等于1的圆与所有直线相交，A对；

圆心为(0,2)，半径小于1的圆与所有直线不相交，B对；

圆心为(0,2)，半径等于1的圆与所有直线都相切，C对；

因为M中的直线与以(0,2)为圆心，半径为1的圆相切，所以M中的直线所能围成的正三角形面积不都相等．如图△ABC与△ADE均为等边三角形而面积不等．答案：A、B、C

8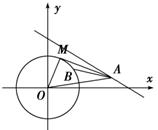．设圆O：x²+y²＝，直线l：x+3y－8＝0，点A∈l，使得圆O上存在点B，且∠OAB＝30°(O为坐标原点)，则点A的横坐标的取值范围是________．

解析：依题意点A∈l，设A(x₀，)．过点A作圆O的切线，切点为M，

则∠OAM≥∠OAB＝30°.从而sin∠OAM≥sin30°＝，即≥sin30°＝，就是|OA|²≤4(|OM|²)＝，x₀²+()²≤，5x₀²－8x₀≤0，解得x₀∈[0，]．

答案：[0，]

7．(2010年宁波调研)已知圆C：x²+y²+bx+ay－3＝0(a、b为正实数)上任意一点关于直线l：x+y+2＝0的对称点都在圆C上，则+的最小值为________．

解析：由题意，知圆心在直线上，所以－+(－)+2＝0，

∴+＝1，则(+)(+)＝1++≥1+2　 ＝1+.

6．(2009年高考全国卷Ⅱ)已知AC、BD为圆O：x²+y²＝4的两条相互垂直的弦，垂足为M(1，)，则四边形ABCD的面积的最大值为________．

解析：设圆心O到AC、BD的距离分别为d₁、d₂，则d₁²+d₂²＝OM²＝3.

四边形ABCD的面积S＝|AB|·|CD|＝2≤8－(d₁²+d₂²)＝5.

5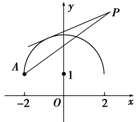．若集合A＝{(x，y)|y＝1+}，B＝{(x，y)|y＝k(x－2)+4}．当集合A∩B有4个子集时，实数k的取值范围是________________．

解析：A∩B有4个子集，即A∩B有2个元素，∴半圆x²+(y－1)²＝4(y≥1)与过P(2,4)点，斜率为k的直线有两个交点，如图：A(－2,1)，k_PA＝，过P与半圆相切时，k＝，∴<k≤.

答案：＜k≤

4．过点A(11,2)作圆x²+y²+2x－4y－164＝0的弦，其中弦长为整数的共有__条．

解析：方程化为(x+1)²+(y－2)²＝13²，圆心为(－1,2)，到点A(11,2)的距离为12，最短弦长为10，最长弦长为26，所以所求直线条数为2+2×(25－10)＝32(条)．答案：32

3．已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，a与b的夹角为60°，直线xcosα+ysinα＝0与圆(x+cosβ)²+(y+sinβ)²＝的位置关系是________．

解析：cos60°＝cosα·cosβ+sinα·sinβ＝cos(α－β)，

d＝＝|cos(α－β)|＝>＝r.答案：相离

2．(2010年秦州质检)已知直线y＝－x与圆x²+y²＝2相交于A、B两点，P是优弧AB上任意一点，则∠APB＝____________.

解析：弦心距长为，半径为，所以弦AB所对的圆心角为，又因为同弦所对的圆周角是圆心角的一半，所以∠APB＝.答案：

1．直线ax+by+b－a＝0与圆x²+y²－x－3＝0的位置关系是________．

解析：直线方程化为a(x－1)+b(y+1)＝0，过定点(1，－1)，代入圆的方程，左侧小于0，则定点在圆内，所以直线与圆总相交．答案：相交