
3. (1) 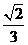 ,
, 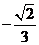 ,
0,
,
0, 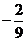
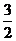 , 0,
, 0, 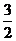 , 0;
, 0;
2, 1, 3, 2;
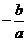 ,
, 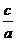 .
.
(2)已知: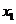 和
和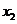 是方程
是方程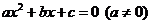 的两个根,
的两个根,
那么,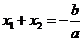 ,
, 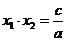 .
.
2. 解:(1)由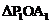 是等腰直角三角形,得
是等腰直角三角形,得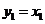 ,则有
,则有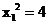 ,故
,故
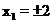 (负舍),点
(负舍),点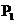 (2,2)。
(2,2)。
(2)由题意知
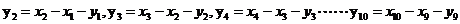
又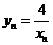 ,则
,则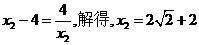
则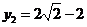 ,故
,故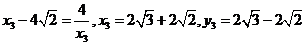 ,同理,依次得
,同理,依次得
1.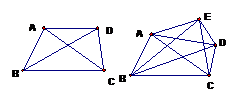 解:通过观察凸四边形和五边形对角线的条数,可得到凸八边形的对角线条数应该是20条.思考过程:凸n边形每个顶点不能和它自己以及它的两个邻点作对角线,所以可做的对角线条数是(n-3), 凸n边形有n个顶点,所以可做n(n-3)条,由于对角线AB和BA是同一条,所以凸n边形共有
解:通过观察凸四边形和五边形对角线的条数,可得到凸八边形的对角线条数应该是20条.思考过程:凸n边形每个顶点不能和它自己以及它的两个邻点作对角线,所以可做的对角线条数是(n-3), 凸n边形有n个顶点,所以可做n(n-3)条,由于对角线AB和BA是同一条,所以凸n边形共有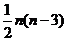 条对角线.当n=8时,有
条对角线.当n=8时,有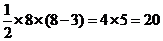 条对角线.
条对角线.
23. 24. 6n;25. 37;26. (2)27. 88; 28. 18.45;29. 30. 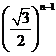 ;31. .60;32. 10
;31. .60;32. 10
1. 83
2. 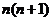 3. 28;4. 3n+1; 5. 30,199;6. 18;7. (
3. 28;4. 3n+1; 5. 30,199;6. 18;7. ( ,n) ;8.
,n) ;8. 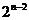 9.
Sn =4(n-1);10. 4或9或15个小正方形;11. 136;12.
9.
Sn =4(n-1);10. 4或9或15个小正方形;11. 136;12. 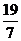 ;13. 65 ;14.
;13. 65 ;14.  ;15.
;15. 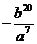 ;
;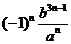 ;16. 8;17. 37;18.
2051;19. 15;20. (3,0);21.
;16. 8;17. 37;18.
2051;19. 15;20. (3,0);21. 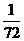 ;22. 26
;22. 26
1.A 2.C 3.D 4.C 5.B 6.C 7.C 8.C 9.A 10.B 11.B 12.A 13.B 14.A 15.C
9.操作与探索(2008桂林市)正方形ABCD的边长为4,BE∥AC交DC的延长线于E。
(1)如图1,连结AE,求△AED的面积。
(2)如图2,设P为BE上(异于B、E两点)的一动点,连结AP、CP,请判断
四边形APCD的面积与正方形ABCD的面积有怎样的大小关系?并说明理由。
(3)如图3,在点P的运动过程中,过P作PF⊥BC交AC于F,将正方形ABCD折叠,使点D与点F重合,其折线MN与PF的延长线交于点Q,以正方形的BC、BA为X轴、Y轴建立平面直角坐标系,设点Q的坐标为(X,Y),求Y与X之间的函数关系式。
探索规律答案
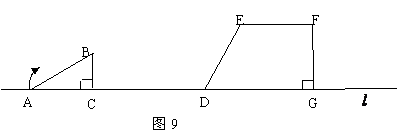
8. (2008湖南常德市)如图9,在直线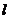 上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O
,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O
,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
(1)旋转:将△ABC绕点C顺时针方向旋转900,请你在图中作出旋转后的对应图形
△A1B1C,并求出AB1的长度;
(2)翻折:将△A1B1C沿过点B1且与直线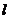 垂直的直线翻折,得到翻折后的对应图形
垂直的直线翻折,得到翻折后的对应图形
△A2B1C1,试判定四边形A2B1DE的形状?并说明理由;
(3)平移:将△A2B1C1沿直线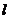 向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
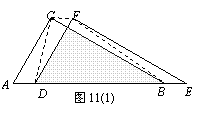
7.(2008湖南益阳市)
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图11(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.

(2)如图11(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
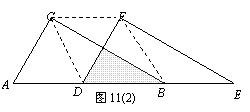
(3)如图11(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.

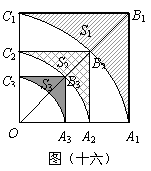
6.(2008年湖南省邵阳市)如图(十六),正方形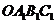 的边长为1,以
的边长为1,以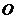 为圆心、
为圆心、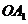 为半径作扇形
为半径作扇形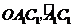 与
与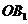 相交于点
相交于点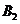 ,设正方形
,设正方形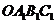 与扇形
与扇形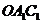 之间的阴影部分的面积为
之间的阴影部分的面积为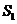 ;然后以
;然后以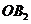 为对角线作正方形
为对角线作正方形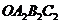 ,又以
,又以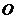 为圆心,、
为圆心,、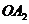 为半径作扇形
为半径作扇形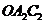 ,
,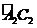 与
与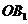 相交于点
相交于点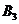 ,设正方形
,设正方形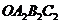 与扇形
与扇形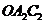 之间的阴影部分面积为
之间的阴影部分面积为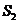 ;按此规律继续作下去,设正方形
;按此规律继续作下去,设正方形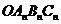 与扇形
与扇形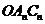 之间的阴影部分面积为
之间的阴影部分面积为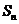 .
.
(1)求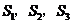 ;
;
 (2)写出
(2)写出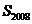 ;
;
(3)试猜想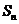 (用含
(用含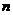 的代数式表示,
的代数式表示,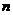 为正整数).
为正整数).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com