17．(09年江苏卷)丘吉尔曾说过：“斯大林是一个世上无出其右的最大的独裁者，他接过俄国时，俄国只有木犁，而当他撒手人寰时，俄国已拥有核武器”苏联之所以能取得如丘吉尔所说的这一重大成就，主要是因为 D

　 A．充分调动了农民和工人的生产积极性

　 B．适时纠正了经济政策中存在的弊端　

C．合理地吸收了西方国家的经济建设经验

　 D．开创并实行了高度集中的计划经济体制

[答案]D

22.(09年广东卷B) 列宁曾讲过：“我们用‘强攻’办法，即用最简单、迅速、直接的办法实行社会主义的生产和分配原则的尝试已告失败。”这里的“尝试”是指

A.十月革命　 B.斯大林模式　 C.新经济政策　 D.战时共产主义政策

[答案]D

[解析]十月革命是暴力推翻资产阶级政权，斯大林模式是在列宁去世以后由斯大林建立，新经济政策是部分的恢复利用商品货币关系来发展经济的成功的经济政策。苏俄共产党领导试图通过战时共产主义政策直接过渡到共产主义，最后遭到了失败。

[考点定位]本题考查的是苏联社会主义建设。

34．(09年广东文基卷)美国学者在《俄罗斯史》中写道：勃列日涅夫政府基本上只是试图作表面的改革，而不考虑从根本上进行改革。对这句话理解正确的是(　 )

A．勃列日涅夫开创了苏联改革的先河

B．勃列日涅夫把改革限制在政治方面

C．勃列日涅夫不打算触动斯大林模式

D．勃列日涅夫首次建立市场经济体制　

[答案]C

15.(09年山东卷) 20世纪30年代初，苏联领导人曾在一次演讲时强调：“已经是布尔什维克自己成为专家的时候了……技术决定一切”这主要是着眼于(　 )

A. 推行战时共产主义政策　　　　　　　 B. 实施新经济政策

C. 发展农业集体经济　　　　　　　　　 D. 进行工业化建设

[答案]D

4．人造卫星(只讨论绕地球做匀速圆周运动的人造卫星)

和星球表面上的物体不同，人造卫星所受的万有引力只有一个作用效果，就是使它绕星球做匀速圆周运动，因此万有引力等于向心力。又由于我们定义重力是由于地球的吸引而使物体受到的力，因此可以认为对卫星而言，

(1)人造卫星的线速度和周期。人造卫星的向心力是由地球对它的万有引力提供的，因此有： ，由此可得到两个重要的结论：和。可以看出，人造卫星的轨道半径r、线速度大小v和周期T是一一对应的，其中一个量确定后，另外两个量也就唯一确定了。离地面越高的人造卫星，线速度越小而周期越大。

(2)近地卫星。近地卫星的轨道半径r可以近似地认为等于地球半径R，又因为地面附近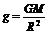，所以有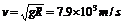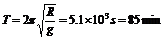，。它们分别是绕地球做匀速圆周运动的人造卫星的最大线速度和最小周期。

(3)同步卫星。“同步”的含义就是和地球保持相对静止(又叫静止轨道卫星)，所以其周期等于地球自转周期，既T=24h，根据(1)可知其轨道半径是唯一确定的，经过计算可求得同步卫星离地面的高度为h=3.6×10⁷m≈5.6R_地(三万六千千米)，而且该轨道必须在地球赤道的正上方，卫星的运转方向必须是由西向东。

在轨道上，向心力等于引力。卫星的线速度随轨道半径的增大而减小。(动能虽然小了，势能却增大了，所以卫星在较高的轨道上运行需要有更大的机械能。)

[例13]“神舟三号”顺利发射升空后，在离地面340km的圆轨道上运行了108圈。运行中需要多次进行“轨道维持”。所谓“轨道维持”就是通过控制飞船上发动机的点火时间和推力的大小方向，使飞船能保持在预定轨道上稳定运行。如果不进行轨道维持，由于飞船受轨道上稀薄空气的摩擦阻力，轨道高度会逐渐降低，在这种情况下飞船的动能、重力势能和机械能变化情况将会是

A．动能、重力势能和机械能都逐渐减小

B．重力势能逐渐减小，动能逐渐增大，机械能不变

C．重力势能逐渐增大，动能逐渐减小，机械能不变

D．重力势能逐渐减小，动能逐渐增大，机械能逐渐减小

解：由于阻力很小，轨道高度的变化很慢，卫星运行的每一圈仍可认为是匀速圆周运动。由于摩擦阻力做负功，根据机械能定理，卫星的机械能减小；由于重力做正功，根据势能定理，卫星的重力势能减小；由可知，卫星动能将增大。这也说明该过程中重力做的功大于克服阻力做的功，外力做的总功为正。答案选D。

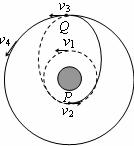
[例14]如图所示，发射同步卫星的一种程序是：先让卫星进入一个近地的圆轨道，然后在P点点火加速，进入椭圆形转移轨道(该椭圆轨道的近地点为近地圆轨道上的P，远地点为同步圆轨道上的Q)，到达远地点时再次自动点火加速，进入同步轨道。设卫星在近地圆轨道上运行的速率为v₁，在P点短时间加速后的速率为v₂，沿转移轨道刚到达远地点Q时的速率为v₃，在Q点短时间加速后进入同步轨道后的速率为v₄。试比较v₁、v₂、v₃、v₄的大小，并用小于号将它们排列起来______。

解：根据题意在P、Q两点点火加速过程中，卫星速度将增大，所以有v₁<v₂、v₃<v₄，而v₁、v₄是绕地球做匀速圆周运动的人造卫星的线速度，它们对应的轨道半径r₁<r₄，所以v₄<v₁。把以上不等式连接起来，可得到结论：v₃<v₄<v₁<v₂。(卫星沿椭圆轨道由P→Q运行时，由于只有重力做负功，卫星机械能守恒，其重力势能逐渐增大，动能逐渐减小，因此有v₃<v₂。)

[例15]欧洲航天局用阿里亚娜火箭发射地球同步卫星。该卫星发射前在赤道附近(北纬5°左右)南美洲的法属圭亚那的库卢基地某个发射场上等待发射时为1状态，发射到近地轨道上做匀速圆周运动时为2状态，最后通过转移、调试，定点在地球同步轨道上时为3状态。将下列物理量按从小到大的顺序用不等号排列：①这三个状态下卫星的线速度大小______；②向心加速度大小______；③周期大小______。

解：①比较2、3状态，都是绕地球做匀速圆周运动，因为r₂<r₃，所以v₃<v₂；比较1、3状态，周期相同，即角速度相同，而r₁<r₃由v=rω，显然有v₁<v₃；因此v₁<v₃<v₂。②比较2、3状态，都是绕地球做匀速圆周运动，因为r₂<r₃，而向心加速度就是卫星所在位置处的重力加速度g=GM/r²∝1/r²，所以a₃<a₂；比较1、3状态，角速度相同，而r₁<r₃，由a=rω²∝r，有a₁<a₃；所以a₁<a₃<a₂。③比较1、2状态，可以认为它们轨道的周长相同，而v₁<v₂，所以T₂<T₁；又由于3状态卫星在同步轨道，周期也是24h，所以T₃=T₁，因此有T₂<T₁=T₃。

[例16]如图所示，用细绳一端系着的质量为M=0.6kg的物体A静止在水平转盘上，细绳另一端通过转盘中心的光滑小孔O吊着质量为m=0.3kg的小球B，A的重心到O点的距离为0.2m。若A与转盘间的最大静摩擦力为f=2N，为使小球B保持静止，求转盘绕中心O旋转的角速度ω的取值范围。(取g=10m/s²)

分析与解：要使B静止，A必须相对于转盘静止--具有与转盘相同的角速度．A需要的向心力由绳拉力和静摩擦力合成。角速度取最大值时，A有离心趋势，静摩擦力指向圆心O；角速度取最小值时，A有向心运动的趋势，静摩擦力背离圆心O。

对于B，T=mg

对于A，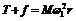

解得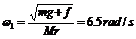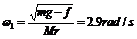；；故2.9rAd/s≤ω≤6.5rAd/s。

[例17]质量为m的小球，由长为l的细线系住，细线的另一端固定在A点，AB是过A的竖直线，E为AB上的一点，且AE=，过E做水平线EF，在EF上钉一铁钉D，如图所示。若线能承受的最大拉力是9mg，现将悬线拉至水平，然后由静止释放，若小球能绕钉子在竖直平面内做圆周运动，求钉子位置在水平线上的取值范围。不计线与钉碰撞时的能量损失。

分析与解：设ED=x，则细线碰到钉子后，做圆周运动的半径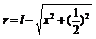。此半径必须满足两个临界条件：

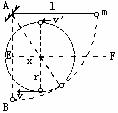
小球通过该圆的最低点时，细线拉力F≤9mg　　　　　　　　 (1)

小球通过该圆的最高点时，小球的速度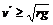　　　　　　 (2)

根据机械能守恒定律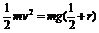，　　　　　　　 　　(3)

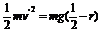　　　　　　　　　 (4)

由牛顿运动定律，　　　　　　　　　　　　 (5)

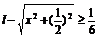联立(1)(3)(5)得，即，所以；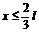

联立(2)(4)得，即，所以；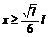

故x的取值范围是。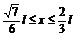

3．万有引力和重力的关系

一般的星球都在不停地自转，星球表面的物体随星球自转需要向心力，因此星球表面上的物体所受的万有引力有两个作用效果：一个是重力，一个是向心力。如图所示，星球表面的物体所受的万有引力的一个分力是重力，另一个分力是使该物体随星球自转所需的向心力。即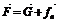

地球表面的物体所受到的向心力f的大小不超过重力的0.35%，因此在计算中可以认为万有引力和重力大小相等。如果有些星球的自转角速度非常大，那么万有引力的向心力分力就会很大，重力就相应减小，就不能再认为重力等于万有引力了。如果星球自转速度相当大，使得在它赤道上的物体所受的万有引力恰好等于该物体随星球自转所需要的向心力，那么这个星球就处于自行崩溃的临界状态了(2003年高考有关中子星问题就是这种情况)。

[例11]中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T＝1/30s。向该中子星的最小密度应是多少才能维持该星体的稳定，不致因自转而瓦解。计等时星体可视为均匀球体。(引力常数G＝6.67×10^－11m³/kg·s²)

解答：考虑中子星赤道处一小块物质，只有当它受到的万有引力大于或等于它随星体一起旋转所需的向心力时，中子星才不会瓦解。

设中子星的密度为ρ，质量为M，半径为R，自转角速度为ω，位于赤道处的小块物质质量为m，则有

GMm/R²＝mω²R

ω＝2π/T

M＝4/3πρR³

由以上各式得ρ＝3π/GT²

代人数据解得ρ＝1.27×10¹⁴kg/m³

[例12]某行星自转周期是6小时。在该行星赤道上称得某物体的重力是同一物体在两极称得的重力的90%，求该行星的平均密度。

解：由已知，该星球赤道上物体所受的向心力是万有引力的10%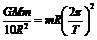，，而星球质量，由以上两式可得ρ=3.03×10³kg/m³

2．双星

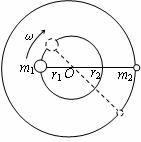
宇宙中往往会有相距较近，质量可以相比的两颗星球，它们离其它星球都较远，因此其它星球对它们的万有引力可以忽略不计。在这种情况下，它们将各自围绕它们连线上的某一固定点做同周期的匀速圆周运动。这种结构叫做双星。

(1)由于双星和该固定点总保持三点共线，所以在相同时间内转过的角度必相等，即双星做匀速圆周运动的角速度必相等，因此周期也必然相同。

(2)由于每颗星的向心力都是由双星间相互作用的万有引力提供的，因此大小必然相等，由F=mrω²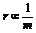可得，可得，，即固定点离质量大的星较近。

(3)列式时须注意：万有引力定律表达式中的r表示双星间的距离，按题意应该是L，而向心力表达式中的r表示它们各自做圆周运动的半径，在本题中为r₁、r₂，千万不可混淆。

当我们只研究地球和太阳系统或地球和月亮系统时(其他星体对它们的万有引力相比而言都可以忽略不计)，其实也是一个双星系统，只是中心星球的质量远大于环绕星球的质量，因此固定点几乎就在中心星球的球心。可以认为它是固定不动的。

万有引力定律的内容：任何两个物体之间都存在相互吸引的力。引力的大小跟两个物体质量的乘积成正比，跟它们之间距离的二次方成反比。

公式：，只适用于质点或质量分布均匀的球体，式中r是质点间或球心间的距离．

基本问题是研究星体(包括人造星体)在万有引力作用下做匀速圆周运动。

1．用万有引力定律求中心星球的质量和密度

当一个星球绕另一个星球做匀速圆周运动时，设中心星球质量为M，半径为R，环绕星球质量为m，线速度为v，公转周期为T，两星球相距r，由万有引力定律有：，可得出。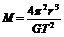

由r、v或r、T就可以求出中心星球的质量；如果环绕星球离中心星球表面很近，即满足r≈R，那么由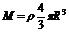可以求出中心星球的平均密度。

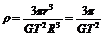3．竖直面内圆周运动最高点处的受力特点及分类

这类问题的特点是：由于机械能守恒，物体做圆周运动的速率时刻在改变，物体在最高点处的速率最小，在最低点处的速率最大。物体在最低点处向心力向上，而重力向下，所以弹力必然向上且大于重力；而在最高点处，向心力向下，重力也向下，所以弹力的方向就不能确定了，要分三种情况进行讨论。

(1)弹力只可能向下，如绳拉球。

这种情况下有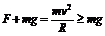，即，否则不能通过最高点。

(2)弹力只可能向上，如车过桥。

在这种情况下有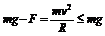：，即，否则车将离开桥面，做平抛运动。

(3)弹力既可能向上又可能向下，如管内转(或杆连球、环穿珠)。

这种情况下，速度大小v可以取任意值。但可以进一步讨论：①当时物体受到的弹力必然是向下的；当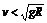时物体受到的弹力必然是向上的；当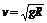时物体受到的弹力恰好为零。②当弹力大小F<mg时，向心力有两解：mg±F；当弹力大小F>mg时，向心力只有一解：F+mg；当弹力F=mg时，向心力等于零或2mg。

[例10]如图所示，杆长为L，球的质量为m，杆连球在竖直平面内绕轴O自由转动，已知在最高点处，杆对球的弹力大小为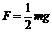，求这时小球的瞬时速度大小。

解：小球所需向心力向下，本题中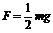＜mg，所以弹力的方向可能向上也可能向下。

(1)若F向上，则，即：。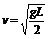

(2)若F向下，则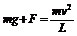，即：。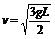

本题是杆连球绕轴自由转动，根据机械能守恒，还能求出小球在最低点的即时速度。

需要注意的是：若题目中说明小球在杆的带动下在竖直面内做匀速圆周运动，则运动过程中小球的机械能不再守恒，这两类题务必分清。

2．描述匀速圆周运动的物理量

物理量有：线速度v、角速度ω、周期T、频率f、转速n、向心加速度a等等。

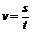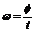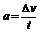，，，，，关系是：，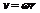

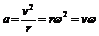
适用于匀速圆周运动和非匀速圆周运动的公式有：；；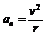

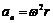只适用于匀速圆周运动的公式有：；

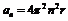
小结：前三个公式是用瞬时量线速度v和角速度ω表示的，因而是普遍适用的。周期T和转速n不是瞬时量，后两个公式只适用于匀速圆周运动。

凡是直接用皮带传动(包括链条传动、摩擦传动)的两个轮子，两轮边缘上各点的线速度大小相等；凡是同一个轮轴上(各个轮都绕同一根轴同步转动)的各点角速度相等(轴上的点除外)。

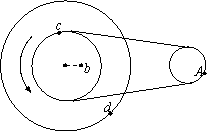
[例8]如图所示装置中，三个轮的半径分别为r、2r、4r，b点到圆心的距离为r，求图中A、b、c、d各点的线速度之比、角速度之比、加速度之比。

解：v_a= v_C，而v_b∶v_C∶v_d =1∶2∶4，所以v_a∶ v_b∶v_C∶v_d =2∶1∶2∶4；ω_a∶ω_b=2∶1，而ω_b=ω_C=ω_d ，所以ω_a∶ω_b∶ω_C∶ω_d =2∶1∶1∶1；再利用a=vω，可得a_a∶a_b∶a_c∶a_d=4∶1∶2∶4

[例9]如图所示，一种向自行车车灯供电的小发电机的上端有一半径r₀=1.0cm的摩擦小轮，小轮与自行车车轮的边缘接触。当车轮转动时，因摩擦而带动小轮转动，从而为发电机提供动力。自行车车轮的半径R₁=35cm，小齿轮的半径R₂=4.0cm，大齿轮的半径R₃=10.0cm。求大齿轮的转速n₁和摩擦小轮的转速n₂之比。(假定摩擦小轮与自行车轮之间无相对滑动)

解：大小齿轮间、摩擦小轮和车轮之间和皮带传动原理相同，两轮边缘各点的线速度大小相等，由v=2πnr可知转速n和半径r成反比；小齿轮和车轮间和轮轴的原理相同，两轮上各点的转速相同。由这三次传动可以找出大齿轮和摩擦小轮间的转速之比n₁∶n₂=2∶175