
3.利用运动的对称性解题
2.巧选参考系求解运动学问题
1.平均速度的求解及其方法应用
① 用定义式: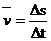 普遍适用于各种运动;②
普遍适用于各种运动;②  =
=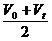 只适用于加速度恒定的匀变速直线运动
只适用于加速度恒定的匀变速直线运动
2.初速为零匀加速直线运动物体追同向匀速直线运动物体
①两者速度相等时有最大的间距 ②位移相等时即被追上
1.匀减速运动物体追匀速直线运动物体。
①两者v相等时,S追<S被追 永远追不上,但此时两者的距离有最小值
②若S追<S被追、V追=V被追 恰好追上,也是恰好避免碰撞的临界条件。追 被追
③若位移相等时,V追>V被追则还有一次被追上的机会,其间速度相等时,两者距离有一个极大值
4、匀变速直线运动
(1)深刻理解:

(2)公式 (会“串”起来)

①根据平均速度定义 =
=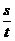 =
=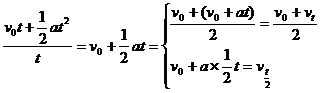
∴Vt/ 2 = =
=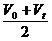 =
=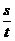
②根据基本公式得Ds = aT2 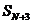 一
一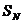 =3 aT2 Sm一Sn=(
m-n) aT2
=3 aT2 Sm一Sn=(
m-n) aT2
推导:
第一个T内
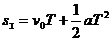 第二个T内
第二个T内
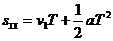 又
又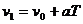
∴Ds =SⅡ-SⅠ=aT2
以上公式或推论,适用于一切匀变速直线运动,记住一定要规定正方向!选定参照物!同学要求必须会推导,只有亲自推导过,印象才会深刻!
(3) 初速为零的匀加速直线运动规律
①在1T末 、2T末、3T末……ns末的速度比为1:2:3……n;
②在1T 、2T、3T……nT内的位移之比为12:22:32……n2;
③在第1T 内、第 2T内、第3T内……第nT内的位移之比为1:3:5……(2n-1); (各个相同时间间隔均为T)
④从静止开始通过连续相等位移所用时间之比为1: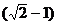 :
: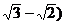 ……(
……(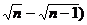
⑤通过连续相等位移末速度比为1: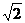 :
: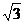 ……
……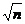
(4) 匀减速直线运动至停可等效认为反方向初速为零的匀加速直线运动.(由竖直上抛运动的对称性得到的启发)。(先考虑减速至停的时间).
(5)竖直上抛运动:(速度和时间的对称)
分过程:上升过程匀减速直线运动,下落过程初速为0的匀加速直线运动.
全过程:是初速度为V0加速度为-g的匀减速直线运动。适用全过程S = Vo t -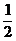 g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
上升最大高度:H = 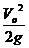 上升的时间:t=
上升的时间:t= 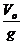
对称性:
①上升、下落经过同一位置时的加速度相同,而速度等值反向
②上升、下落经过同一段位移的时间相等 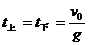 。从抛出到落回原位置的时间:t =2
。从抛出到落回原位置的时间:t =2
(6)图像问题
识图方法:一轴物理量、二单位、三物理意义(斜率、面积、截距、交点等)
图像法是物理学研究常用的数学方法。用它可直观表达物理规律,可帮助人们发现物理规律。借用此法还能帮助人们解决许许多多物理问题。对于诸多运动学、动力学问题特别是用物理分析法(公式法)难以解决的问题,若能恰当地运用运动图像处理,则常常可使运动过程、状态更加清晰、求解过程大为简化。请叙述下列图象的意义.

①、位移-时间图象(s-t图像):
横轴表示时间,纵轴表示位移;
静止的s-t图像在一条与横轴平行或重合的直线上;
匀速直线运动的s-t图像在一条倾斜直线上,所在直线的斜率表示运动速度的大小及符号;
②、速度-时间图像(v-t图像):
横轴表示时,纵轴表示速度;请叙述下列图象的意义.
静止的v-t图像在一条与横轴重合的直线上;
匀速直线运动的v-t图像在一条与横轴平行的直线上;
匀变速直线运的v-t图像在一条倾斜直线上,所在直线的斜率表示加速度大小及符号;
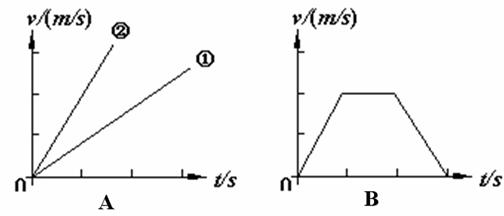 当直线斜率(加速度)与运动速度同号时,物体做匀加速直线运动;
当直线斜率(加速度)与运动速度同号时,物体做匀加速直线运动;
当直线余率(加速度)与运动速度异号时,物体做匀减速直线运动。
匀变速直线运的v-t图像在一条倾斜直线上,面积表示位移
(7)追及和相遇或避免碰撞的问题的求解方法:
关键:在于掌握两个物体的位置坐标及相对速度的特殊关系。
基本思路:分别对两个物体研究,画出运动过程示意图,列出方程,找出时间、速度、位移的关系。解出结果,必要时进行讨论。
追及条件:追者和被追者v相等是能否追上、两者间的距离有极值、能否避免碰撞的临界条件。
讨论:
3、分类

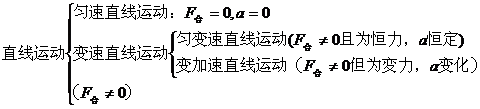
2、基本概念
(1) (2)
(2) (3)
(3)
(4)
1、直线运动的条件:①F合=0或②F合≠0且F合与v共线,a与v共线。(回忆曲线运动的条件)
10.某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为1年以上的概率为p1,寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(Ⅰ)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(Ⅱ)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
(Ⅲ)当p1=0.8,p2=0.3时,求在第二次灯泡更换工作,至少需要更换4只灯泡的概率(结果保留两个有效数字).
本小题主要考查概率的基础知识和运算能力,以及运用概率的知识分析和解决实际问题能力.
解:(I)在第一次更换灯泡工作中,不需要换灯泡的概率为 需要更换2只灯泡的概率为
需要更换2只灯泡的概率为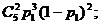
(II)对该盏灯来说,在第1、2次都更换了灯泡的概率为(1-p1)2;在第一次未更换灯泡而在第二次需要更换灯泡的概率为p1(1-p2),故所求的概率为
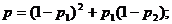
(III)至少换4只灯泡包括换5只和换4只两种情况,换5只的概率为p5(其中p为(II)中所求,下同)换4只的概率为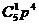 (1-p),故至少换4只灯泡的概率为
(1-p),故至少换4只灯泡的概率为
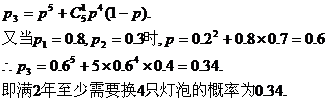
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com