3.连带运动问题

　　 指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的，杆都是不可伸长和压缩的，即绳或杆的长度不会改变，所以解题原则是：把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相同求解。

例6. 如图所示，汽车甲以速度v₁拉汽车乙前进，乙的速度为v₂，甲、乙都在水平面上运动，求v₁∶v₂

解：甲、乙沿绳的速度分别为v₁和v₂cosα，两者应该相等，所以有v₁∶v₂=cosα∶1

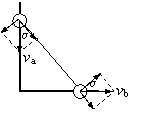例7. 两根光滑的杆互相垂直地固定在一起。上面分别穿有一个小球。小球a、b间用一细直棒相连如图。当细直棒与竖直杆夹角为α时，求两小球实际速度之比v_a∶v_b

解：a、b沿杆的分速度分别为v_acosα和v_bsinα

∴v_a∶v_b= tanα∶1

2.过河问题

　　 如右图所示，若用v₁表示水速，v₂表示船速，则：

①过河时间仅由v₂的垂直于岸的分量v_⊥决定，即，与v₁无关，所以当v₂⊥岸时，过河所用时间最短，最短时间为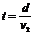也与v₁无关。

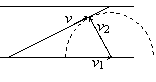②过河路程由实际运动轨迹的方向决定，当v₁＜v₂时，最短路程为d ；当v₁＞v₂时，最短路程程为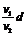(如右图所示)。

1.运动的性质和轨迹

　　 物体运动的性质由加速度决定(加速度得零时物体静止或做匀速运动；加速度恒定时物体做匀变速运动；加速度变化时物体做变加速运动)。

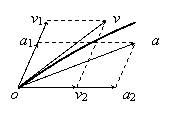　　 物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动；速度和加速度方向成角度时物体做曲线运动)。

　　 两个互成角度的直线运动的合运动是直线运动还是曲线运动？

决定于它们的合速度和合加速度方向是否共线(如图所示)。　　

　　 常见的类型有：

⑴a=0：匀速直线运动或静止。

⑵a恒定：性质为匀变速运动，分为：① v、a同向，匀加速直线运动；②v、a反向，匀减速直线运动；③v、a成角度，匀变速曲线运动(轨迹在v、a之间，和速度v的方向相切，方向逐渐向a的方向接近，但不可能达到。)

⑶a变化：性质为变加速运动。如简谐运动，加速度大小、方向都随时间变化。

2.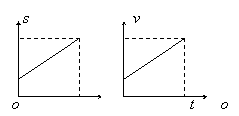v-t图象。能读出s、t、v、a的信息(斜率表示加速度，曲线下的面积表示位移)。可见v-t图象提供的信息最多，应用也最广。

例4. 一个固定在水平面上的光滑物块，其左侧面是斜面AB，右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑，

比较它们到达水平面所用的时间

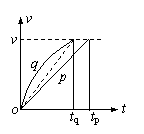　 A.p小球先到　　 B.q小球先到　　 C.两小球同时到　　 D.无法确定

解：可以利用v-t图象(这里的v是速率，曲线下的面积表示路程s)定性地进行比较。在同一个v-t图象中做出p、q的速率图线，显然开始时q的加速度较大，斜率较大；由于机械能守恒，末速率相同，即曲线末端在同一水平图线上。为使路程相同(曲线和横轴所围的面积相同)，显然q用的时间较少。

例5. 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a^/ 同时从管口由静止滑下，问谁先从下端的出口掉出？(假设通过拐角处时无机械能损失)　　　

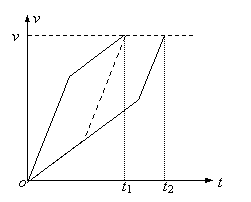解：首先由机械能守恒可以确定拐角处v₁> v₂，而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律，小球的加速度大小a=gsinα，小球a第一阶段的加速度跟小球a^/第二阶段的加速度大小相同(设为a₁)；小球a第二阶段的加速度跟小球a^/第一阶段的加速度大小相同(设为a₂)，根据图中管的倾斜程度，显然有a₁> a₂。根据这些物理量大小的分析，在同一个v-t图象中两球速度曲线下所围的面积应该相同，且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等，如果同时到达(经历时间为t₁)则必然有s₁>s₂，显然不合理。考虑到两球末速度大小相等(图中v_m)，球a^/ 的速度图象只能如蓝线所示。因此有t₁< t₂，即a球先到。

1.s-t图象。能读出s、t、v 的信息(斜率表示速度)。

5.一种典型的运动

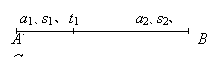经常会遇到这样的问题：物体由静止开始先做匀加速直线运动，紧接着又做匀减速直线运动到静止。用右图描述该过程，可以得出以下结论：

①　 ②

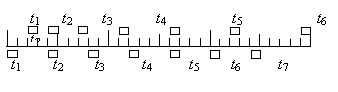例1. 两木块自左向右运动，现用高速摄影机在同一底片上多次曝光，记录下木块每次曝光时的位置，如图所示，连续两次曝光的时间间隔是相等的，由图可知

A.在时刻t₂以及时刻t₅两木块速度相同

B.在时刻t₁两木块速度相同

C.在时刻t₃和时刻t₄之间某瞬间两木块速度相同

D.在时刻t₄和时刻t₅之间某瞬时两木块速度相同

解：首先由图看出：上边那个物体相邻相等时间内的位移之差为恒量，可以判定其做匀变速直线运动；下边那个物体明显地是做匀速运动。由于t₂及t₅时刻两物体位置相同，说明这段时间内它们的位移相等，因此其中间时刻的即时速度相等，这个中间时刻显然在t₃、t₄之间，因此本题选C。

例2. 在与x轴平行的匀强电场中，一带电量q=1.0×10^-8C、质量m=2.5×10^-3kg的物体在光滑水平面上沿着x轴作直线运动，其位移与时间的关系是x＝0.16t－0.02t²，式中x以m为单位，t以s为单位。从开始运动到5s末物体所经过的路程为　　　　 m，克服电场力所做的功为　　　　 J。

解：须注意：本题第一问要求的是路程；第二问求功，要用到的是位移。

将x＝0.16t－0.02t²和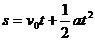对照，可知该物体的初速度v₀=0.16m/s，加速度大小a=0.04m/s²，方向跟速度方向相反。由v₀=at可知在4s末物体速度减小到零，然后反向做匀加速运动，末速度大小v₅=0.04m/s。前4s内位移大小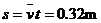，第5s内位移大小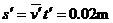，因此从开始运动到5s末物体所经过的路程为0.34m，而位移大小为0.30m，克服电场力做的功W=mas₅=3×10^-5J。

例3. 物体在恒力F₁作用下，从A点由静止开始运动，经时间t到达B点。这时突然撤去F₁，改为恒力F₂作用，又经过时间2t物体回到A点。求F₁、F₂大小之比。

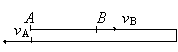解：设物体到B点和返回A点时的速率分别为v_A、v_B， 利用平均速度公式可以得到v_A和v_B的关系。再利用加速度定义式，可以得到加速度大小之比，从而得到F₁、F₂大小之比。

　　 画出示意图如右。设加速度大小分别为a₁、a₂，有：

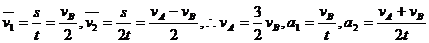
　 　∴a₁∶a₂=4∶5，∴F₁∶F₂=4∶5

　　 特别要注意速度的方向性。平均速度公式和加速度定义式中的速度都是矢量，要考虑方向。本题中以返回A点时的速度方向为正，因此AB段的末速度为负。

4.初速为零的匀变速直线运动

①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……

②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……

③前1米、前2米、前3米……所用的时间之比为1∶∶∶……

④第1米、第2米、第3米……所用的时间之比为1∶∶()∶……

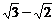对末速为零的匀变速直线运动，可以相应的运用这些规律。

3.初速度为零(或末速度为零)的匀变速直线运动

做匀变速直线运动的物体，如果初速度为零，或者末速度为零，那么公式都可简化为：　

　　 　，　 　，　 　，　

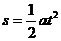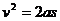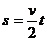
以上各式都是单项式，因此可以方便地找到各物理量间的比例关系。

2.匀变速直线运动中几个常用的结论

①Δs=aT ²，即任意相邻相等时间内的位移之差相等。可以推广到s_m-s_n=(m-n)aT ²

②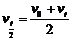，某段时间的中间时刻的即时速度等于该段时间内的平均速度。

　　，某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。

可以证明，无论匀加速还是匀减速，都有。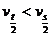

1.常用公式有以下四个

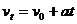
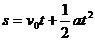
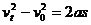
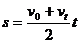
⑴以上四个公式中共有五个物理量：s、t、a、v₀、v_t，这五个物理量中只有三个是独立的，可以任意选定。只要其中三个物理量确定之后，另外两个就唯一确定了。每个公式中只有其中的四个物理量，当已知某三个而要求另一个时，往往选定一个公式就可以了。如果两个匀变速直线运动有三个物理量对应相等，那么另外的两个物理量也一定对应相等。

⑵以上五个物理量中，除时间t外，s、v₀、v_t、a均为矢量。一般以v₀的方向为正方向，以t=0时刻的位移为零，这时s、v_t和a的正负就都有了确定的物理意义。