
1,正反词语:
下面给出一些关键词的否定:
|
正面 语词 |
等于 |
大于 |
小于 |
是 |
全 |
都是 |
至少一个 |
至多 一个 |
|
否定 |
不等于 |
不大于 (小于等于) |
不小于 (大于等于) |
不是 |
不全 |
不都是 |
一个也 没有 |
至少 两个 |
2,对数函数图象
|
图 象 |
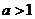 |
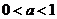 |
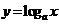
|
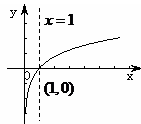
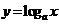

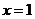
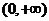

 ,即当
,即当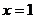 时,
时,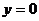
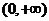 上是减函数
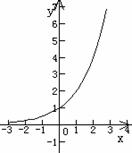
上是减函数3,指数函数图象
|
|
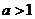 |
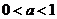 |
|
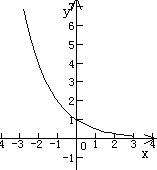
图象 |
 |
 |
|
性质 |
(1)定义域: |
|
(2)值域: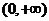 |
||
(3)过点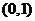 ,即 ,即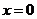 时 时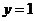 |
||
(4)在 上是增函数 上是增函数 |
(4)在 上是减函数 上是减函数 |
4,同角三角函数的关系图象
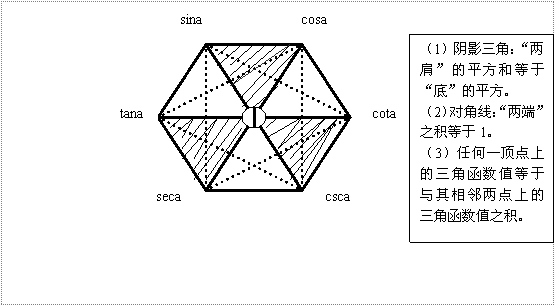
5,正弦、余弦、正切函数图象
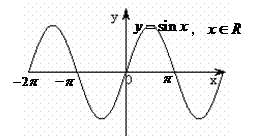
Y=tanx

|
函 数 |
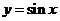 |
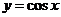 |
Y = tanx |
|
定义域 |
R |
R |
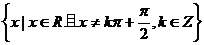 |
|
值域 |
[-1,1] |
[-1,1] |
R |
|
对称点 |
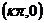 |
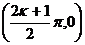 |
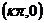 |
|
对称轴 |
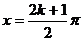 |
 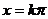 |
无 |
|
增区间 |
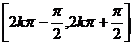 |
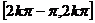 |
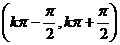 |
|
减区间 |
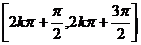 |
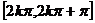 |
无 |
|
周期性 |
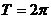 |
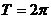 |
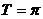 |
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
附:反三角函数的主值区间:
|
反三角函数 |
 |
 |
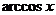 |
|
定义域 |
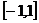 |
R |
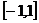 |
|
主值区间(值域) |
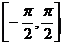 |
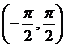 |
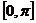 |
8,圆的三种方程:
|
名称 |
形式 |
圆心 |
半径 |
条件 |
|
标准方程 |
 |
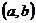 |
r |
r>0 |
|
参数方程 |
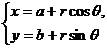 |
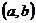 |
r |
r>0 |
|
一般方程 |
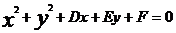 |
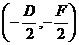 |
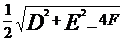 |
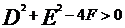 |
(1)点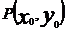 与圆
与圆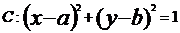 的位置关系:
的位置关系:
若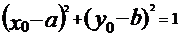 ,则点
,则点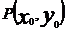 在圆C上;
在圆C上;
若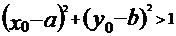 ,则点
,则点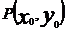 在圆C外;
在圆C外;
若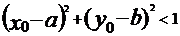 ,则点
,则点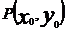 在圆C内;
在圆C内;
(2)直线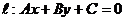 与圆
与圆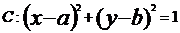 的位置关系:
的位置关系:
①联立 
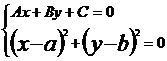 消去不偿失得:
消去不偿失得:
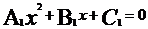 ,则
,则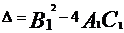 ,直线
,直线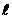 与圆
与圆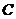 的位置关系:
的位置关系:
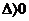 相交;
相交; 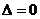 相切 ;
相切 ;
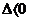 相离 。
相离 。
② 圆心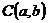 到直线
到直线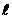 的距离为
的距离为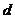 ,则直线
,则直线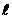 与圆
与圆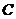 的位置关系:
的位置关系:
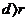 相交;
相交;
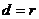 相切 ;
相切 ;
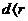 相离 。
相离 。
(3)圆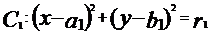 与圆
与圆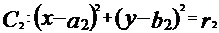 的位置关系:
的位置关系:
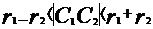 相交;
相交;
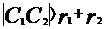 相离;
相离;
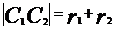 外切;
外切;
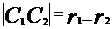 内切。
内切。
(4)半弦长与弦心距的平方和等于半径的平方。
(5)弦的垂直平分线经过圆心。
(6)圆心到切线的距离等于半径。
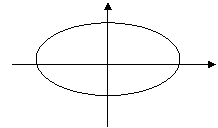
9,椭圆
|
第一定义 |
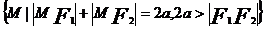 |
|
||
|
第二定义 |
 |
|
||
|
方 程 |
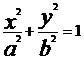 |
 |
|
|
|
图 象 |
 |
 |
|
|
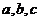 关 系 关 系 |
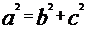 |
|
||
|
范 围 |
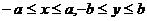 |
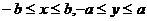 |
|
|
|
顶 点 |
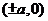 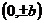 |
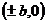 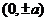 |
|
|
|
对 称
性 |
关于 轴成轴对称、关于原点成中心对称 轴成轴对称、关于原点成中心对称 |
|
||
|
离 心
率 |
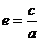 |
|
||
|
焦 点 |
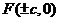 |
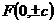 |
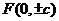 |
|
|
准 线 |
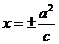 |
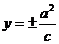 |
|
|
|
焦点三角形面积公式 |
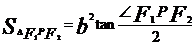 |
|
||
(1)点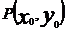 与椭圆C:
与椭圆C: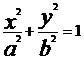 的位置关系:
的位置关系:
若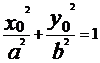 ,则点
,则点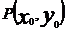 在椭圆C上;
在椭圆C上;
若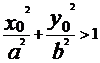 ,则点
,则点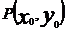 在椭圆C外;
在椭圆C外;
若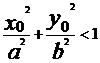 ,则点
,则点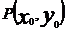 在椭圆C内;
在椭圆C内;
(2)直线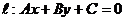 与椭圆C:
与椭圆C: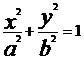 的位置关系判断:用
的位置关系判断:用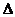 法。
法。
10,双曲线
|
第一定义 |
 |
|
|
第二定义 |
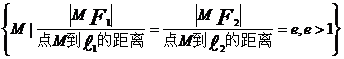 |
|
|
方 程 |
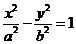 ( (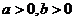 ) ) |
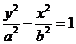 ( (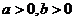 ) ) |
|
图 象 |
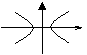 |
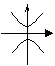 |
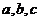 关 系 关 系 |
 |
|
|
范 围 |
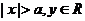 |
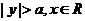 |
|
顶 点 |
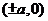 |
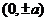 |
|
对 称 性 |
关于 轴成轴对称、关于原点成中心对称 轴成轴对称、关于原点成中心对称 |
|
|
渐 近 线 |
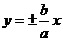 |
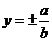 |
|
离 心 率 |
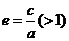 |
|
|
焦 点 |
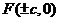 |
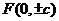 |
|
准 线 |
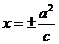 |
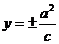 |
|
焦点三角形面积公式 |
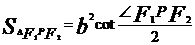 |
11,抛物线
|
定义 |
平面内,到定点F的距离与到定直线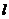 的距离相等的点的轨迹。 的距离相等的点的轨迹。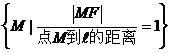 |
|||
|
方程 |
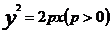 |
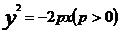 |
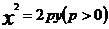 |
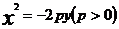 |
|
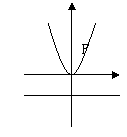
图
形 |
  |
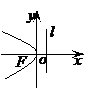 |
 |
 |
|
焦点坐标 |
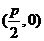 |
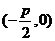 |
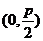 |
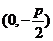 |
|
准线方程 |
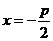 |
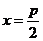 |
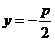 |
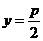 |
|
范围 |
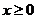 |
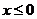 |
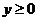 |
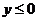 |
|
对称性 |
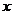 轴 轴 |
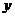 轴 轴 |
||
|
顶点 |
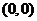 |
|||
|
离心率 |
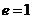 |
1,指数运算性质:
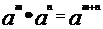 ;
; 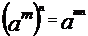 ;
; 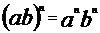 (
(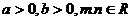 )
)
2,对数运算性质:
 logaM +
logaM + logaN =
logaN = logaMN ;logaM - logaN =
logaMN ;logaM - logaN = loga
loga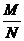 ;alogaN=N ;logaM =
;alogaN=N ;logaM = ;
;
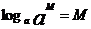 (
(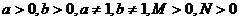 )。
)。
3,等差数列:
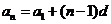 ;
; 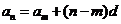 ;
;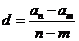
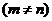 ;
;
若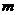 ,
,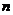 ,
,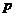 ,
,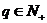 且
且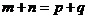 ,则
,则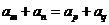 ;
;
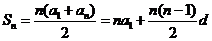 。
。
 是等差数列
是等差数列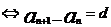 (d为常数)
(d为常数) 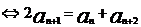
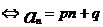 (p,q为常数)
(p,q为常数)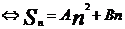 (A,B为常数)
(A,B为常数)
4,等比数列:
 ;
; 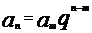 (
(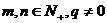 ) ;
) ;
若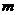 ,
,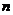 ,
,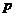 ,
,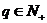 且
且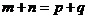 ,则
,则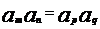
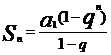 ;
;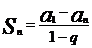 (
(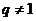 );
);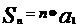 (q=1);
(q=1);
 是等比数列
是等比数列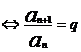 (q为常数)
(q为常数) 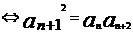
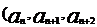 不等于0)
不等于0) 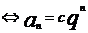 (c,q为非0常数)
(c,q为非0常数)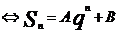 (A,B为常数,A+B=
-1)
(A,B为常数,A+B=
-1)
5, 绝对值不等式定理:
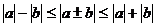 。
。
6,弧长公式与扇形面积公式:
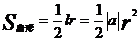 。
。
7,诱导公式:
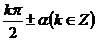 与a的三角函数间的关系式即为诱导公式,口诀:“函数名奇变偶不变;符号看象限”。
与a的三角函数间的关系式即为诱导公式,口诀:“函数名奇变偶不变;符号看象限”。
8,同关系角公式:
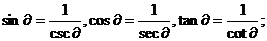
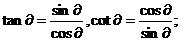
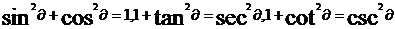
9,和(差)角公式:
 ;
; 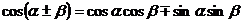 ;
;
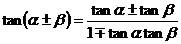 。
。
10,倍角公式:
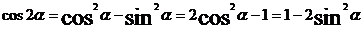 ;
;
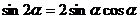 ;
; 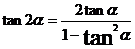 。
。
化简公式:
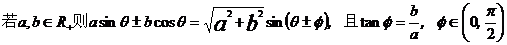 。
。
11,不等式的性质:
(1)三条公理: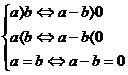
(2)五条基本性质:
对称性: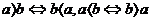
传递性: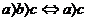
移向法则: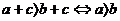
乘法法则: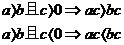
倒数法则: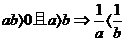
(3)六条基本性质:
加法:
减法: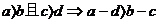
乘法:
除法: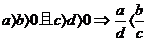
乘方: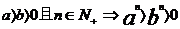
开方: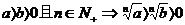
(4)均值不等式:
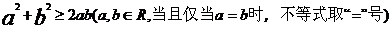
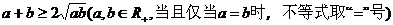
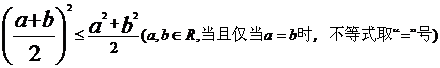
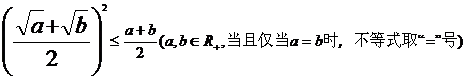
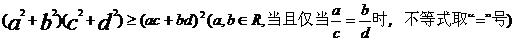
12,不等式的解法:
(1)一元二次不等式的解集与一元二次方程的对应关系:
 |
解集 |
||
|
|
△>0 |
△=0 |
△<0 |
|
ax2+bx+c=0 (a>0) |
x=x1 或x=x2 |
x1=x2=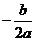 |
无实数根 |
|
ax2+bx+c>0 |
{x|x<x1或x>x2} |
{x|x≠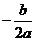 } } |
R |
|
ax2+bx+c<0 |
{x|x1<x<x2} |
Ø |
ø |
(2)分式不等式:
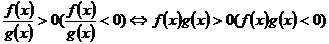 ;
;
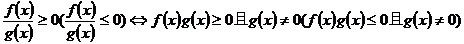 。
。
(3)无理不等式:
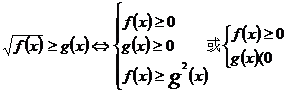 ;
;
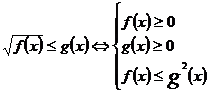
(4)指数不等式:
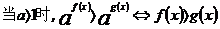 ;
;
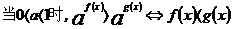 。
。
(5)对数不等式:
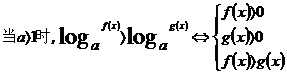
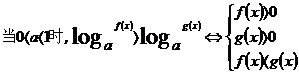
(6)绝对值不等式:
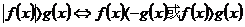 ;
;
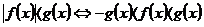 ;
;
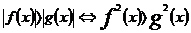
13,正余弦定理:
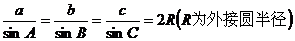

14,三角形面积公式:
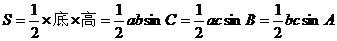
15,平面向量:
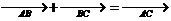 ;
; 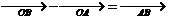
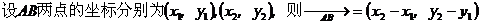
设a= (x1,y1)b= (x2,y2)则: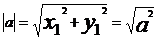 ;
;
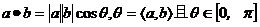 ;a.b= x1 x2 + y1 y2
;a.b= x1 x2 + y1 y2
a∥b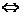 a=
a=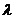 b
b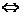 x1 y2 - x2 y1 = 0
x1 y2 - x2 y1 = 0
a⊥b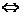 a.b=0
a.b=0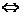 x1 x2 +y1 y2 = 0
x1 x2 +y1 y2 = 0
16,平移公式:
如果点P(x,y)按向量a=(h,k)平移至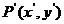 则
则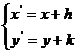
17,定比分点公式:
A(x1,y1),B(x2,y2),点P(x,y)分AB所成的比为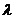 则
则
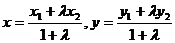
18,距离公式:
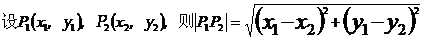
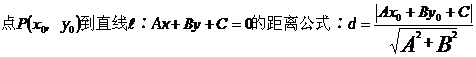
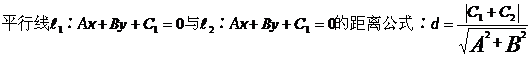 19,斜率公式:
19,斜率公式:
设直线 (A≠0)的倾斜角为а(а≠900),方向向量为v=(a,b)(a≠0),直线
(A≠0)的倾斜角为а(а≠900),方向向量为v=(a,b)(a≠0),直线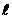 上有两个点P1(x1,y1)P2(x2,y2)(x1≠x2),则直线
上有两个点P1(x1,y1)P2(x2,y2)(x1≠x2),则直线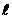 的斜
率
的斜
率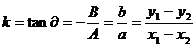 。
。
20,两直线平行或垂直的充要条件:
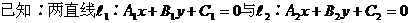
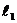 ∥
∥ 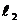
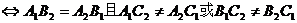
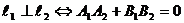 。
。
21,弦长公式:
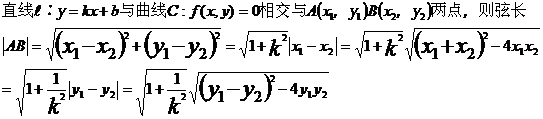 22,概率公式:
22,概率公式:
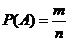 ;
;
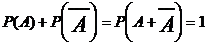 ;
;
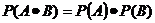 ;
; 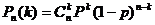
23,平面的基本性质:
公理1: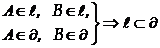
公理2: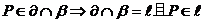
公理3:点A,B,C不公线,则有且只有一个平面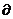 ,使
,使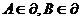 ,且
,且 。
。
推论1: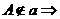 有且只有一个平面
有且只有一个平面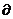 ,使
,使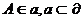 。
。
推论2: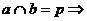 有且只有一个平面
有且只有一个平面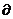 ,使
,使 。
。
推论3: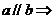 有且只有一个平面
有且只有一个平面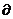 ,使
,使 。:
。:
公理4: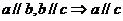 。
。
24,等角定理:
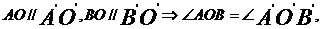 或
或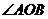 与
与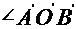 互补。
互补。
25,直线和平面平行的判定和性质定理:
判定定理:若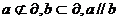 ,则
,则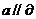 。
。
性质定理:若 ,则
,则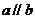 。
。
26,直线和平面垂直的判定和性质定理:
判定定理:若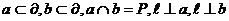 ,则
,则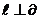 。
。
性质定理:若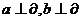 ,则
,则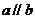 。
。
27,两个平面平行的判定和性质定理:
判定定理:若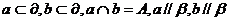 ,则
,则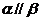 。
。
性质定理:若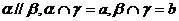 ,则
,则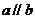 。
。
28,两个平面垂直的判定和性质定理:
判定定理:直线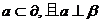 ,则
,则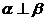 。
。
性质定理: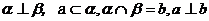 ,则
,则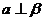 。
。
29,三垂线定理:
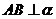 于B,
于B,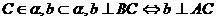 。
。
30,排列数公式:
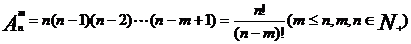 。
。
31,组合数的公式和性质:
公式: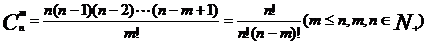
性质1:
性质2: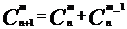 。
。
32,二项式定理:
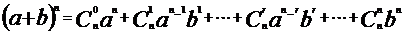
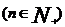 ;
;
二项式系数的和为: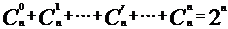 ;
;
二项展开式的通项公式: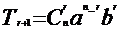
 。
。
33,概率与统计:
(1)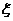 的分布列:
的分布列:
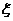 |
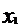 |
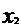 |
。。。 |
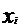 |
。。。 |
|
P |
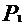 |
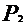 |
。。。 |
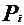 |
。。。 |
(2)二项分布: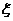 - B(n,p)
- B(n,p)
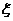 |
0 |
1 |
… |
k |
… |
n |
|
P |
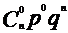 |
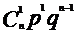 |
… |
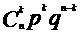 |
… |
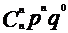 |
(3)期望: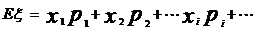
注:①E(a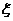 +b)=a.E
+b)=a.E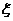 +b ;
+b ;
② 若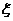 - B(n,p)
, 则E
- B(n,p)
, 则E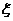 =np .
=np .
(4)标准差: 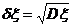
(5)方差: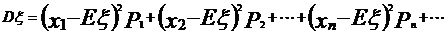
注:①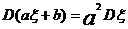 ;
;
② 若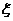 - B(n,p)
, 则D
- B(n,p)
, 则D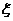 =np(1-p);
=np(1-p);
③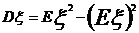
34,无穷等比数列(|q|≤1)的和:
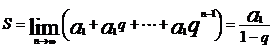 。
。
35,两个重要的极限:
 ,
,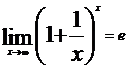 。
。
36,函数导数的四则运算法则:
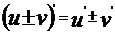 ;
;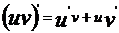 ;
;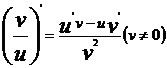
37,导数基本公式:
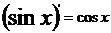 ;
;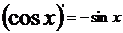 ;
;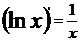 ;
;
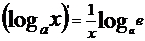 ;
; ;
;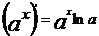 ;
;
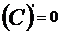 (C为常数) ;
(C为常数) ;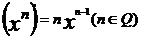 。
。
38,复数运算法则:
(a+bi)±(c+di)=(a±c)+(b±d)i ; (a+bi)(c+di)=(ac-bd)+(ad+bc)i ;
(a+bi)÷(c+di)= 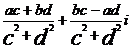
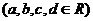 ;
;
39,复数三角形式的运算法则:
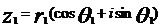 ,
,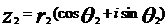 ,
,
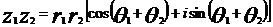 ;
;
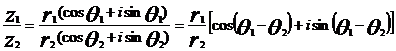 ;
;
乘方: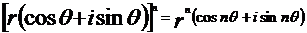
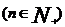 ;
;
开方: ,其中
,其中
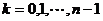
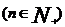 。
。
4、列方程求解
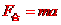 ①物体受两个力: 合成法
①物体受两个力: 合成法
②物体受多个力: 正交分解法(沿运动方向和垂直于运动方向分解)
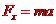 (运动方向)
(运动方向)
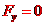 (垂直于运动方向)
(垂直于运动方向)
3、规定正方向或建立直角坐标系,求合力F合
2、进行受力分析和运动状态分析,画出示意图
1、明确研究对象(隔离或整体)
8、不能认为牛一是牛二在合外力为0时的特例。
例4、从牛顿第二定律知道,无论怎样小的力都可以使物体产生加速度。可是我们用力提一个很重的物体时却提不动它,这跟牛顿第二定律有无矛盾?为什么?
答:没有矛盾,从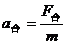 角度来看,因为提不动,所以静止,则合外力为0,所以加速度也为0;从
角度来看,因为提不动,所以静止,则合外力为0,所以加速度也为0;从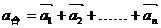 角度来看,物体受三个力,支持力、重力、向上提的力。这三个力产生的加速度相互抵消,所以合加速度也是0。
角度来看,物体受三个力,支持力、重力、向上提的力。这三个力产生的加速度相互抵消,所以合加速度也是0。
例5、某质量为1100kg的汽车在平直路面试车,当达到100km/h的速度时关闭发动机,经过70s停下来,汽车受到的阻力是多大?重新起步加速时牵引力为2000 N,产生的加速度应为多大?假定试车过程中汽车受到的阻力不变。
例6、一个物体,质量是2 kg,受到互成 120°角的两个力F1和F2的作用。这两个力的大小都是10N,这两个力产生的加速度是多大?
7、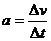 是定义式、度量式;
是定义式、度量式;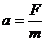 是决定式。两个加速度公式,一个是纯粹从运动学(现象)角度来研究运动;一个从本质内因进行研究。 就像农民看云识天气,掌握天气规律,但并不知道云是如何形成的,为什么不同的云代表不同的天气。就像知道有加速度却不知道为何会有。
是决定式。两个加速度公式,一个是纯粹从运动学(现象)角度来研究运动;一个从本质内因进行研究。 就像农民看云识天气,掌握天气规律,但并不知道云是如何形成的,为什么不同的云代表不同的天气。就像知道有加速度却不知道为何会有。
6、牛二适用于宏观低速运动的物体
5、牛二只适用于惯性参考系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com