
(1)必做题:(见后)
(2)选做题:(见后)
(3)思考题:
1.我们所学的性质是通过图象观察得到的,这些性质能不能用推理的方法得到呢 ? 如利用指数函数的值域和数值变化证明指数函数的单调性等 。
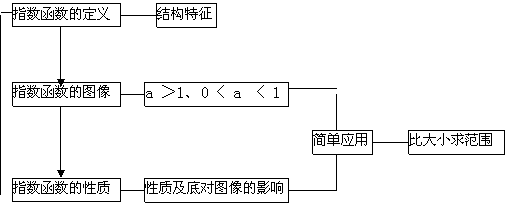
(五)小结归纳,拓展深化
(1)通过本节课的学习,你学到了那些知识?
 |
|||
|
|||
(2)你又掌握了哪些学习方法?
(3)你能将指数函数的学习与实际生活联系起来吗?
(四)当堂训练,共同提高
例 1: 比较下列各题中两个值的大小 :
(l)1.72.5,173;
(2)0.8-01,0.8-02;
(3)(0.3)-0.3,(0.2)-0.3
(4)1.70.3,0.93.1
解 :(1) 考察指数函数 y=1.7x, 由于底数 1.7〉1, 所以指数函数 y=1.7X 在 R 上是增函数
因为 2.5〈 3 , 所以 1.72.5〈1.73
(2) 考察指数函数 y =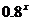 ,
由于底数0〈0.8〈 l, 所以指数函数y =
,
由于底数0〈0.8〈 l, 所以指数函数y =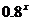 在 R 上是减函数。
在 R 上是减函数。
因为 -0.1 〉-0.2,
所以 0.8-0.1〈 0.8-0.2
同底数幂比大小时 , 可构造指数函数,利用单调性比大小 .
(3) 观察图像可得,(0.3)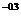 〈( 0.2)
〈( 0.2)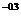 不同底数幂在比大小时 , 可利用多个指数函数图象比大小
不同底数幂在比大小时 , 可利用多个指数函数图象比大小
(4) 由指数函数的性质知
1.703 〉 1.7 0 =1,
093.1〈 0.90 =l
即 1.70.3 〉0.93.1〈 1,
所以 1.70.3 〉0.93.1
不同底数幂比大小时 , 可利用图象法或利用中间变量 ( 多选0,1)
例2:已知下列不等式
, 比较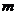 和
和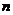 的大小 :
的大小 :
(l )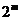 〈
〈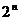
(2)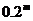 〉
〉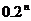
(3)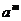 <
<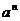 (
( 〉0)
〉0)
解:
(1) 因为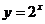 是一个单调递增函数,所以由题意
是一个单调递增函数,所以由题意
 〈
〈 
(2) 因为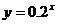 是一个单调递增函数, 所以由题意
是一个单调递增函数, 所以由题意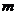 〈
〈 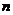
(3)
当 〉1时
〉1时 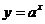 是一个单调递增函数,所以此时
是一个单调递增函数,所以此时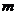 〈
〈 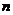
当0< <1时
<1时 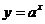 是一个单调递减函数, 所以此时
是一个单调递减函数, 所以此时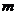 〉
〉 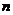
(三)深入探究,加深理解
|
|
教学环节与问题设计 |
设计目的 |
||
|
(1) 教师设疑,深入探究 |
教师提问: 对于底这个变化量是否与图像之间存在着联系呢? |
通过问题,让学生的思考进一步深入 |
||
|
(2)观察图像,合作讨论 |
 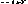 y y
1. x 0 2.教师带领学生观察几何画板的动态演示 3.学生分小组交流探讨,派代表阐述观点 |
在此环节中,教师并不急于给出结论,而是让学生充分经历知识的形成过程,从而形成自己对本节课难点的理解和解决策略,培养学生的直觉和感悟能力。 |
||
|
(3) 得出结论,加深理解 |
(1)在第一象限中图像越往上底越大;(2 )当底互为倒数时,图像关于y轴对称, |
让学生体会数学中蕴含的规律性和对称美。感悟结论的过程中实现本节课难点的突破。 |
(二) 发现问题、探究新知
|
|
教学环节与问题设计 |
设计目的 |
|||||||||||||
|
(1)以问题为载体,探求新知 |
提出问题: (1) 如何判断一个函数为指数函数 ? (2) 怎样得到指数函数的图象 ? (3) 指数函数有哪些性质 ? |
注重学生思维习惯的养成,即应从哪些方面,那些角度去探索一个具体函数。 |
|||||||||||||
|
(2)合作交流,动手画图 |
学生分成四个小组,分别作出 (1) 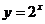 (2)
(2) (3) 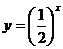 (4) (4)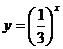 教师在多媒体上给予展示 |
复习描点画图,体验合作交流。利用多媒体,给予学生直观认识。 |
|||||||||||||
|
(3)观察图像,研究性质 |
此时教师组织学生讨论,并引导学生观察图像的特点。进而得出a>1和0<a<1这两种情况在图像上的特点。并填写下方
表格: |
将具体化为抽象,并感受了对底的分类讨论的思维方式,通过几何画板的演示验证学生对底的猜测,从而达到了重点的突破。 |
(一)创设情境、形成概念
2.计算并完成以下表格
|
n |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
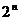 |
|
|
|
|
|
|
|
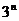 |
|
|
|
|
|
|
|
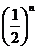 |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
教学环节与问题设计 |
设计目的 |
|
第一环节:创设游戏情境,设疑激趣 |
学生分成小组,动手折纸 , 观察对折次数与所得纸的层数的关系。得出折一次为 2 层纸,折两次为
22层纸 , 折三次为 23 层纸 ...得对折次数x与所得纸的层数 y 的关系式为 y =2x |
设疑激趣,在学生动手操作的过程中激发学生学习热情和探索新知的欲望。 |
|
第二环节:引出具体定义,探究条件 |
定义: 一般地 , 函数 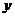 = =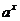 ( (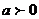  且 且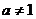 ) 叫做指数函数 , 其中 ) 叫做指数函数 , 其中 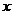 是自变量 , 定义域为 R. 是自变量 , 定义域为 R.问题:为何对  有这样的要求? 有这样的要求?(1) 如果  =0 当 =0 当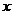 >0 时 >0 时 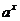 恒等于 0; 当 恒等于 0; 当 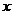 〈 0 时 , 〈 0 时 , 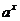 无意义 无意义(2) 如果  〈 0 时,比如: 〈 0 时,比如: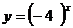 ,对 ,对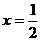 及 及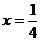 等都无意义 等都无意义(3) 如果  =1, 则原函数变成 =1, 则原函数变成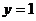 是一个常数 , 研究价值不大。 是一个常数 , 研究价值不大。 |
对a的范围的具体分析,有利于学生对指数函数一般形式的掌握,同时为后面研究函数的图象和性质埋下了伏笔。 |
|
第三环节:运用定义,判断具体函数 |
能否判断下列函数哪些是指数函数吗? (1) 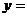 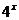 (2) (2) (3)  (4)
(4) 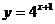 |
打破学生对定义的轻视并使学生头脑中不断完善对定义理解 |
1.若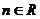 时
,
时
,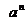 总有意义 , 求
总有意义 , 求 的范围 ?
的范围 ?
重点是指数函数的图像、性质及简单应用;
难点是指数函数图象和性质的发现过程,及指数函数图像与底的关系。
(1) 认知目标 : 理解指数函数的定义 , 掌握指数函数的图象、性质及其简单应用 ;
(2) 能力目标 : 通过指数函数的图象和性质的教学 , 培养学生观察、分析、
归纳等思维能力和数形结合的数学思想
(3) 情感目标 : 认识事物的普遍联系与相互转化 , 激发学生学习数学的兴趣 ,努力培养学生的创新意识 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com