4．图上距离是12厘米，实地距离是3600千米，该图的比例尺为

A． 1：3000万　　 B． 1：300万　　 C．1：30万　　　 D．1：3万

3．下图是等高距相同的四幅地形图，有关a、b、c、d四处坡度大小的说法，正确的是

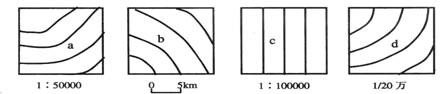
A．a>c>d>b　　 　B．a=b=c=d　　　 C．b>d>c>a　 　　D．无法确定

2．对下列比例尺相同的等高线地形图，判断正确的是

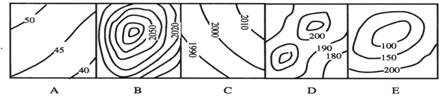
A．坡度由大到小为BEDCA　 　　　　B．坡度由大到小为BDECA

C．坡度由大到小为ACDBE　　　　　 　D．坡度由大到小为EBDCA

下列各题的四个选项中只有一个是正确的。请将你认为正确的一项的答案填写在题后的表格内。

1．下图中虚线或字母表示地形部位。下列选项中，地形部位名称排序与图序相符的是

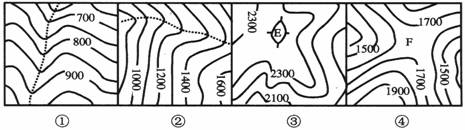
A．①山谷②山脊③鞍部④山顶　 　　　B．①山谷②山谷③山顶④鞍部

C．①山谷②山脊③山顶④鞍部　 　　D．①山脊②山脊③山顶④鞍部

22.(本小题满分14分)(2010·长郡模拟)已知函数f(x)＝x⁴+ax³+2x²+b(x∈R)，其中a，b∈R.

(1)当a＝－时，讨论函数f(x)的单调性；

(2)若函数f(x)仅在x＝0时处有极值，求a的取值范围；

(3)若对于任意的a∈[－2,2]，不等式f(x)≤1在[－1,1]上恒成立，求b的取值范围.

解：(1)f′(x)＝4x³+3ax²+4x＝x(4x²+3ax+4).

当a＝－时，f′(x)＝x(4x²－10x－4)

＝2x(2x－1)(x－2).

令f′(x)＝0，解得x₁＝0，x₂＝，x₂＝2.

当x变化时，f′(x)，f(x)的变化情况如下表：

x	(－∞，0)	0		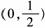		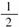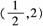2	(2，+∞)
f′(x)	－	0	+	0	－	0	+
f(x)	↘	极小值	↗	极大值	↘	极小值	↗

所以f(x)在(0，)，(2，+∞)内是增函数，在(－∞，0)，(，2)内是减函数.

(2)f′(x)＝x(4x³+3ax+4)，显然x＝0不是方程4x³+3ax+4＝0的根.

为使f(x)仅在x＝0处有极值，必须4x²+3ax+4≥0，即有Δ＝9a²－64≤0.

解此不等式，得－≤a≤.这时，f(0)＝b是唯一极值.

因此满足条件的a的取值范围是[－，].

(3)由条件a∈[－2,2]，可知Δ＝9a²－64＜0，从而4x²+3ax+4＞0恒成立.

当x＜0时，f′(x)＜0；当x＞0时，f′(x)＞0.

因此函数f(x)在[－1,1]上的最大值是f(1)与f(－1)两者中的较大者.

为使对任意的a∈[－2,2]，不等式f(x)≤1在[－1,1]上恒成立，当且仅当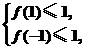

即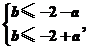在a∈[－2,2]上恒成立.

所以b≤－4，因此满足条件的b的取值范围是(－∞，－4].

21.(本小题满分12分)已知向量a＝(x²－1，－1)，b＝(x，y)，当|x|＜时，有a⊥b；当|x|≥ 时，a∥b.

(1)求函数y＝f(x)的解析式；

(2)求函数y＝f(x)的单调递减区间；

(3)若对|x|≥ ，都有f(x)≤m，求实数m的最小值.

解：(1)当|x|＜时，由 a⊥b，得a·b＝(x²－1)x－y＝0，

即y＝x³－x(|x|＜)；

当|x|≥时，由a∥b，得y＝(|x|≥).

∴f(x)＝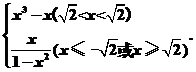

　(2)当|x|＜时，由y′＝3x²－1＜0，解得－＜x＜，

当|x|≥时，y′＝＝＞0，

∴函数f(x)的单调递减区间为(－，).

(3)对∀x∈(－∞，－]∪[，+∞)，都有f(x)≤m，即m≥，

由(2)知当|x|≥时，y′＝＞0，

∴函数f(x)在(－∞，－]和[，+∞)上都单调递增，

f(－)＝＝，f()＝＝－，

当x≤－时，y＝＞0，∴0＜f(x)≤f(－)＝，

同理可得，当x≥时，有－≤f(x)＜0，

综上所述，对∀x∈(－∞，－]∪[，+∞)，f(x)取得最大值，

∴实数m的最小值为.

20.(本小题满分12分)已知函数f(x)＝－x³+3x²+9x+a，

(1)求f(x)的单调区间；

(2)若f(x)在区间[－2,2]上的最大值为20，求函数f(x)在该区间上的最小值.

解：(1)f′(x)＝－3x²+6x+9，令f′(x)＜0，解得x＜－1或x＞3，所以函数f(x)的单调递减区间为(－∞，－1)，(3，+∞)；

令f′(x)＞0，解得－1＜x＜3，所以函数f(x)的单调递增区间为(－1,3).

(2)因为f(－2)＝8+12－18+a＝2+a，f(2)＝－8+12+18+a＝22+a，

所以f(2)＞f(－2).

因为在区间(－1,3)上，f′(x)＞0，所以f(x)在(－1,2)上单调递增.

又由于f(x)在(－2，－1)上单调递减，

因此f(2)和f(－1)分别是f(x)在区间[－2,2]上的最大值和最小值，

于是有22+a＝20，解得a＝－2，

故f(x)＝－x³+3x²+9x－2，

因此f(－1)＝－7，即函数f(x)在区间[－2,2]上的最小值为－7.

19.(本小题满分12分)是否存在这样的实数a，使函数f(x)＝x²+(3a－2)x+a－1在区间[－1,3]上与x轴恒有一个交点，且只有一个交点.若存在，求出范围，若不存在，说明理　　　

由.

解：若实数a满足条件，则只需f(－1)·f(3)≤0即可.

f(－1)·f(3)＝(1－3a+2+a－1)·(9+9a－6+a－1)＝4(1－a)(5a+1)≤0.所以a≤－或a≥1.

检验：(1)当f(－1)＝0时，a＝1.所以f(x)＝x²+x.令f(x)＝0，即x²+x＝0.得x＝0或x＝－1.

方程在[－1,3]上有两根，不合题意，故a≠1.

(2)当f(3)＝0时，a＝－，此时f(x)＝x²－x－.令f(x)＝0，即x²－x－＝0，解之得x＝－或x＝3.方程在[－1,3]上有两根，不合题意，故a≠－.

综上所述，a＜－或a＞1.

18.(本小题满分12分)已知函数f(x)＝x²+2ax+2，x∈[－5,5].

(1)当a＝－1时，求f(x)的最大值与最小值；

(2)求实数a的取值范围，使y＝f(x)在区间[－5,5]上是单调函数.

解：(1)当a＝－1时，f(x)＝x²－2x+2＝(x－1)²+1，

当x＝1时，f(x)取最小值为1，当x＝－5时，f(x)取最大值为37，所以f(x)的最大值是37；最小值是1.

(2)由于函数的对称轴是x＝－a，要使函数在区间[－5,5]上是单调函数，必须且只需满足|a|≥5，

故所求的a的取值范围是a≤－5或a≥5.

17.(本小题满分12分)(2010·东北师大附中模拟)已知函数f(x)＝2^x，g(x)＝+2.

(1)求函数g(x)的值域；

(2)求满足方程f(x)－g(x)＝0的x的值.

解：(1)g(x)＝+2＝()^|x|+2，

因为|x|≥0，所以0＜()^|x|≤1，即2＜g(x)≤3，

故g(x)的值域是(2,3].

(2)由f(x)－g(x)＝0得2^x－－2＝0，

当x≤0时，显然不满足方程，即只有x＞0满足2^x－－2＝0，

整理得(2^x)²－2·2^x－1＝0，(2^x－1)²＝2，

故2^x＝1±，

因为2^x＞0，所以2^x＝1+，即x＝log₂(1+).