
1.骑自行车的人沿着直线从静止开始运动,运动后,在第1 s、2 s、3 s、4 s内,通过的路程分别为1 m、2 m、3 m、4 m,有关其运动的描述正确的是
A.4 s内的平均速度是2.5 m/s
B.在第3、4 s内平均速度是3.5 m/s
C.第3 s末的即时速度一定是3 m/s
D.该运动一定是匀加速直线运动
[例1]一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站,求汽车从甲站到乙站的平均速度?
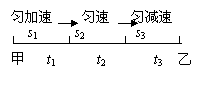 解析:起动阶段行驶位移为:
解析:起动阶段行驶位移为:
s1=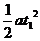 ……(1)
……(1)
匀速行驶的速度为: v= at1 ……(2)
匀速行驶的位移为: s2 =vt2 ……(3)
刹车段的时间为: s3 = ……(4)
……(4)
汽车从甲站到乙站的平均速度为:
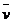 =
=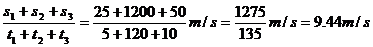
[例2]汽车以加速度为2m/s2的加速度由静止开始作匀加速直线运动,求汽车第5秒内的平均速度?
解析:此题有三解法:
(1)用平均速度的定义求:
第5秒内的位移为:
s = 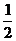 a t52 -
a t52 -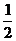 at42 =9 (m)
at42 =9 (m)
第5秒内的平均速度为: v=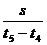 =
=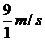 =9 m/s
=9 m/s
(2)用推论v=(v0+vt)/2求:v=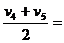
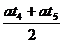 =
=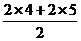 m/s=9m/s
m/s=9m/s
(3)用推论v=vt/2求。第5秒内的平均速度等于4.5s时的瞬时速度:
v=v4.5= a´4.5=9m/s
[例3]一物体由斜面顶端由静止开始匀加速下滑,最初的3秒内的位移为s1,最后3秒内的位移为s2,若s2-s1=6米,s1∶s2=3∶7,求斜面的长度为多少?
解析:设斜面长为s,加速度为a,沿斜面下滑的总时间为t 。则:
斜面长: s = 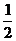 at2 …… ( 1)
at2 …… ( 1)
前3秒内的位移:s1
= 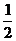 at12 ……(2)
at12 ……(2)
|


 后3秒内的位移:
s2 =s -
后3秒内的位移:
s2 =s -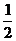 a (t-3)2 …… (3)
a (t-3)2 …… (3)
|
s1∶s2 = 3∶7 …… (5)
解(1)-(5)得:a=1m/s2 t= 5s s=12 . 5m
[例4]物块以v0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间?
解析:物块作匀减速直线运动。设A点速度为VA、B点速度VB,加速度为a,斜面长为S。
 A到B:
vB2 - vA2 =2asAB ……(1)
A到B:
vB2 - vA2 =2asAB ……(1)
vA = 2vB ……(2)
B到C: 0=vB + at0 ……..(3)
解(1)(2)(3)得:vB=1m/s
a= -2m/s2
D到C 0 - v02=2as ……(4)
s= 4m
从D运动到B的时间:
D到B: vB =v0+ at1 t1=1.5秒
D到C再回到B:t2 = t1+2t0=1.5+2´0.5=2.5(s)
[例5]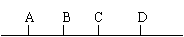 一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?
解:设AB=s1、BC=s2、CD=s3 则:
s2-s1=at2 s3-s2=at2
两式相加:s3-s1=2at2
由图可知:L2-L1=(s3+s2)-(s2+s1)=s3-s1
则:a =
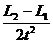
2.匀变速直线运动中几个常用的结论
①Δs=aT 2,即任意相邻相等时间内的位移之差相等。可以推广到sm-sn=(m-n)aT 2
②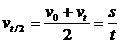 ,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
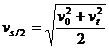 ,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
可以证明,无论匀加速还是匀减速,都有 。
。
点评:运用匀变速直线运动的平均速度公式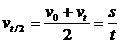 解题,往往会使求解过程变得非常简捷,因此,要对该公式给与高度的关注。
解题,往往会使求解过程变得非常简捷,因此,要对该公式给与高度的关注。
1.常用公式有以下四个
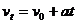
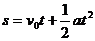
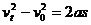

点评:
(1)以上四个公式中共有五个物理量:s、t、a、v0、vt,这五个物理量中只有三个是独立的,可以任意选定。只要其中三个物理量确定之后,另外两个就唯一确定了。每个公式中只有其中的四个物理量,当已知某三个而要求另一个时,往往选定一个公式就可以了。如果两个匀变速直线运动有三个物理量对应相等,那么另外的两个物理量也一定对应相等。
(2)以上五个物理量中,除时间t外,s、v0、vt、a均为矢量。一般以v0的方向为正方向,以t=0时刻的位移为零,这时s、vt和a的正负就都有了确定的物理意义。
21.(10分)如图14所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度屿对轻绳的拉力F,并描绘出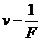 图象。假设某次实验所得的图象如图15所示,其中线段么B与
图象。假设某次实验所得的图象如图15所示,其中线段么B与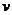 轴平行,它反映了被提升重物在第一个时间段内
轴平行,它反映了被提升重物在第一个时间段内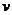 和
和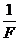 的关系;线段粥的延长线过原点,它反映了被提升重物在第二个时间段内
的关系;线段粥的延长线过原点,它反映了被提升重物在第二个时间段内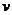 和
和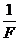 的关系;第三个时间段内拉力F和速度出句为C点所对应的大小保持不变,因此图象上没有反映。实验中还测得重物由静止开始经过
的关系;第三个时间段内拉力F和速度出句为C点所对应的大小保持不变,因此图象上没有反映。实验中还测得重物由静止开始经过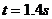 ,速度增加到
,速度增加到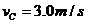 ,此后物体做匀速运动。取重力加速度
,此后物体做匀速运动。取重力加速度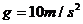 ,绳重及一切摩擦和阻力均可忽略不计。
,绳重及一切摩擦和阻力均可忽略不计。
(1)在提升重物的过程中,除了重物的质量和所受重力保持不变以外,在第一个时间段内和第二个时间段内还各有一些物理量的值保持不变。请分别指出第一个时间段内和第二个时间段内所有其他保持不变的物理量,并求出它们的大小;
(2)求被提升重物在第一个时间段内和第二个时间段内通过的总路程。

20.(10分)课间休息时,同学业们常用摸高比赛来消除疲惫,振奋精神。一质量为60kg的男同学竖直各上跳起,在将要离地时,他的重心高了0.4m,接下来重心又继续升高了0.8m而到达跳跃的最高点。若他蹬地的那段时间是0.2s(空气阻力不计,取g=10m/s2)求:
(1)该男同学的起跳速率?
(2)在起跳过程中,该同学做功的平均功率?
(3)在起跳过程中,该同学蹬地的平均作用力?
19.(10分)一质量不计的直角形支加要两端分别固定着质量均为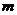 的小球A和B,支架的两直角边长度分别为
的小球A和B,支架的两直角边长度分别为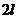 和
和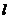 ,支架可绕固定的水平轴O在竖直平面内无摩擦转动,如图13所示。开始时OA边处于水平位置,由静止释放,重力加速度为
,支架可绕固定的水平轴O在竖直平面内无摩擦转动,如图13所示。开始时OA边处于水平位置,由静止释放,重力加速度为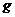 ,求:
,求:
(1)A球转到竖直位置时,其速度多大?
(2)A球转到竖直位置的过程中,轻杆对A球做的功。
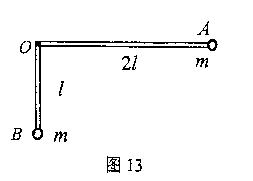
18.(8分)某排球场的俯视图如图12所示,立体图如图13所示,场地全长为a、宽为b。球网离地面的高度为h。某队员在自己一方边线处跳起来发球,设他的击球点在么的正上方,击出的球初速度沿水平方向,球在空中运动时受到的空气阻力可以忽略,球可视为质点。计算时取a=18m,b=8m,h=2m。
(1)要使球落在对方的阴影区域的后边线上,他击球时球至少离地面多高?
(2)如果他的击球点正是上一问求出的最小高度,他击出的球的初速度在什么范围内,
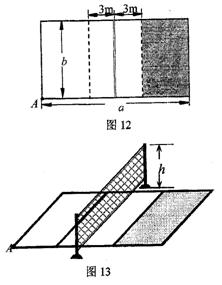 球可以恰好落在对方场地的后边线上?
球可以恰好落在对方场地的后边线上?
17.(8分)某行星探测器在喷气发动机推力作用下从所探测的行星表面竖直升空,当其速度达到80m/s时,发动机突然发生故障而关闭。已知该行星的半径为R=5.0×106m,第一宇宙速度是5.0×103m/s。探测器总质量的变化、行星对探测器的引力随高度的变化、行星自转的影响、行星表面的气体对探测器的影响都忽略不计。求:
(1)该行行星表面附近物体自由下落的加速度;
(2)发动机关闭后探测器能上升的最大高度。
16.(8分)
如图11所示,质量为m的金属块放在水平地面上,在与水平方向成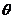 角斜向上、大小为F的拉力作用下,以速度
角斜向上、大小为F的拉力作用下,以速度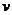 向右做匀速直线运动。重力加速度为g。求:
向右做匀速直线运动。重力加速度为g。求:
(1)金属块与地面间的动摩擦因数;
(2)如果从某时刻起撤去拉力,则撤去拉力后金属块在地面上还能滑行的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com