
2、溶液中溶质的质量分数计算的有关公式(注意单位统一):
(1)溶液的质量=溶质的质量+溶剂的质量=溶液的体积×溶液的密度
(1)溶质的质量分数= 的质量÷ 的质量×100%
(2)溶液的稀释(浓缩):
依据:溶液的稀释(浓缩)前后溶质的质量 。如有溶液Ag,其溶质的质量分数为a%,稀释(浓缩)成溶质的质量分数为b%的溶液Bg,则:Ag×a% =Bg×b%
(4)同溶质不同溶质的质量分数的溶液混合:
依据:混合溶液的质量 混合前各溶液的质量之和,混合溶液中溶质的质量 混合前各溶液中溶质的质量之和。如Ag溶质的质量分数为a%的溶液与Bg溶质的质量分数为b%的溶液混合得到Cg溶质的质量分数为的溶液,则有下列关系:
Ag + Bg = Cg Ag×a% + Bg×b% = Cg×c%
(5)饱和溶液中溶质的质量分数和溶解度的换算:
饱和溶液中溶质的质量分数=--------×100%
溶液是由溶质和溶剂组成的,我们常用溶质的质量分数来定量的表示溶液的组成。
1、溶解度与溶质的质量分数比较
|
|
溶 解 度 |
溶质质量分数 |
|
定 义 |
|
|
|
表示意义 |
①物质溶解性大小的定量表示。 ②表示某温度时的饱和溶液中溶质的质量与溶剂的质量关系。 |
①是溶液浓稀的定量表示。 ②表示某溶液中溶质的质量与溶液的质量关系。 |
|
温度要求 |
与温度 关 |
与温度 关 |
|
溶剂的量 |
在 g溶剂中 |
溶剂的量不一定是100g |
|
溶液类型 |
一定是 溶液 |
饱和溶液与不饱和溶液均可 |
|
单 位 |
克(g) |
比值无单位。常用百分数(%)表示 |
|
计算公式 |
溶解度(S)=------×100g |
溶质的质量分数=----×100% |
2、知道溶解度与溶质的质量分数的区别。会进行饱和溶液中溶质的质量分数和溶解度的换算。
1、记住溶质的质量分数的定义,熟练掌握有关溶质质量分数的计算。
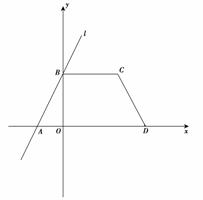
13、如图,直线l:y=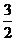 x+3交x轴、y轴于A、B点,四边形ABCD为等腰梯形,BC∥AD,且D点坐标为(6,0).
x+3交x轴、y轴于A、B点,四边形ABCD为等腰梯形,BC∥AD,且D点坐标为(6,0).
(1)求:A、B、C点坐标;
(2)若直线l沿x轴正方向平移m个(m>0)单位长度,与AD、BC 分别交于N、M点,当四边形ABMN的面积为12个单位面积时,求m的值;
(3)如果B点沿BC方向,从B到C运动,速度为每秒2个单位长度,A点同时沿AD方向,从A到D运动,速度为每秒3个单位长度,经过n秒的运动,A到达A′处,B到达B′处,问:是否能使得A′B′平分∠BB′D?若能,请求出n的值;若不能,请说明理由.
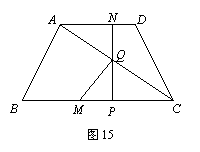
12、已知:如图15,四边形ABCD是等腰梯形,其中AD∥BC,AD=2,BC=4,AB=CD=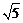 .点M从点B开始,以每秒2个单位长的速度向点C运动;点N从点D开始,以每秒1个单位长的速度向点A运动,若点M,N同时开始运动,点M与点C不重合,运动时间为t(t>0).过点N作NP垂直于BC,交BC于点P,交AC于点Q,连结MQ.
.点M从点B开始,以每秒2个单位长的速度向点C运动;点N从点D开始,以每秒1个单位长的速度向点A运动,若点M,N同时开始运动,点M与点C不重合,运动时间为t(t>0).过点N作NP垂直于BC,交BC于点P,交AC于点Q,连结MQ.
(1)用含t的代数式表示QP的长;
(2)设△CMQ的面积为S,求出S与t的函数关系式;
(3)求出t为何值时,△CMQ为等腰三角形.
(说明:问题(3)是额外加分题,加分幅度为1-4分)
11、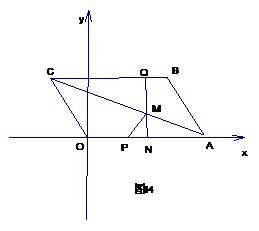 在如图14所示的直角坐标系中, □ABCO的点A(4,0)、B(3,2).点P从点O出发,以2单位/秒的速度向点A运动.同时点Q由点B出发,以1单位/秒的速度向点C运动,当其中一点到达终点时,另一点也随之停止.过点Q作QN⊥x轴于点N,连结AC交NQ于点M,连结PM.设动点Q运动的时间为t秒
在如图14所示的直角坐标系中, □ABCO的点A(4,0)、B(3,2).点P从点O出发,以2单位/秒的速度向点A运动.同时点Q由点B出发,以1单位/秒的速度向点C运动,当其中一点到达终点时,另一点也随之停止.过点Q作QN⊥x轴于点N,连结AC交NQ于点M,连结PM.设动点Q运动的时间为t秒
(1)点C的坐标为______________;
(2)点M的坐标为__________________(用含t的代数式表示).
(3)求ΔPMA的面积S与时间t的函数关系式;是否存在t的值,使ΔPMA的面积最大.若存在求出t的值;若不存在说明理由.
10、小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图(1),垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
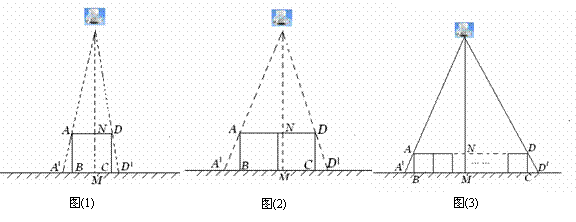
(2)不改变(1)中灯泡的高度,将两个边长为30cm的正方形框架按图(2)摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图(3)摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
9、如图12,Rt△ABC中,∠C=90°,按题目所给条件及要求将相应的直角三角形,分割成若干个全等的并且分别与原三角形相似的三角形.画出图形并简要说明理由.
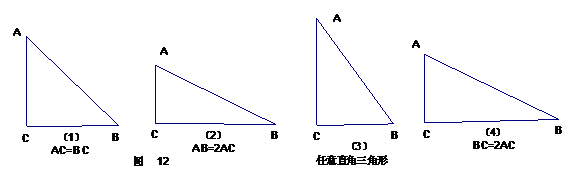 第(1)图AC=BC将ΔABC分割成2个三角形;第(2)图AB=2AC将ΔABC分割成3个三角形;第(3)图将ΔABC分割成4个三角形;第(4)图BC=2AC将ΔABC分割成5个三角形;
第(1)图AC=BC将ΔABC分割成2个三角形;第(2)图AB=2AC将ΔABC分割成3个三角形;第(3)图将ΔABC分割成4个三角形;第(4)图BC=2AC将ΔABC分割成5个三角形;
8、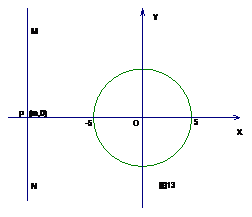 如图13,在平面直角坐标系中,以O为圆心,5个单位为半径画圆.直线MN经过x轴上一动点P(m,0)且垂直于x轴,当P点在x轴上移动时,直线MN也随着平行移动.按下面条件求m的值或范围
如图13,在平面直角坐标系中,以O为圆心,5个单位为半径画圆.直线MN经过x轴上一动点P(m,0)且垂直于x轴,当P点在x轴上移动时,直线MN也随着平行移动.按下面条件求m的值或范围
(1)如果⊙O上任何一点到直线MN的距离都不等于3;(2)如果⊙O上有且只有一点到直线MN的距离等于3;(3)如果⊙O上有且只有二点到直线MN的距离等于3;(4)随着m的变化, ⊙O上到直线MN距离等于3的点的个数还有哪些变化?请说明所有各种情形及对应的m值或范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com