
1.上升和下降(至落回原处)的两个过程互为逆运动,具有对称性。有下列结论:
(1)速度对称:上升和下降过程中质点经过同一位置的速度大小相等、方向相反。
(2)时间对称:上升和下降经历的时间相等。
3.、竖直上抛运动的特点。
竖直上抛运动是匀变速直线运动,其上升阶段为匀减速运动,下落阶段为自由落体运动。它有如下特点:
2、竖直上抛运动:物体获得竖直向上的初速度υ0后仅在重力作用下的运动。
特点:只受重力作用且与初速度方向反向,以初速方向为正方向则a=-g
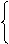 υt=υ0-gt
υt=υ0-gt
运动规律: h=υ0t-gt2/2
υt2=υt2-2gh
对于竖直上抛运动,有分段分析法和整体法两种处理方法。分段法以物体上升到最高点为运动的分界点,根据可逆性可得t上=t下=υ0/g,上升最大高度H=υ02/2g,同一高度速度大小相等,方向相反。整体法是以抛出点为计时起点,速度、位移用下列公式求解:
 υt=υ0-gt
υt=υ0-gt
h=υ0t-gt2/2
注意:若物体在上升或下落中还受有恒空气阻力,则物体的运动不再是自由落体和竖直上抛运动,分别计算上升a上与下降a下的加速度,利用匀变速运动公式问题同样可以得到解决。
[例4]气球以10m/s的速度匀速竖直上升,从气球上掉下一个物体,经17s到达地面。求物体刚脱离气球时气球的高度。(g=10m/s2)1275m
分析与解:可将物体的运动过程视为匀变速直线运动。规定向下方向为正,则物体的
初速度为V0=-10m/s,g=10m/s2
则据h=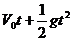 ,则有:
,则有: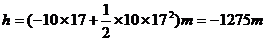
∴物体刚掉下时离地1275m。
1、自由落体运动:物体仅在重力作用下由静止开始下落的运动
特点:只受重力作用,即a=g。从静止开始,即υ0=0
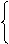 υt=gt
υt=gt
运动规律: S=gt2/2
υt2=2gh
对于自由落体运动,物体下落的时间仅与高度有关,与物体受的重力无关。
初速为零的匀变速直线运动的规律自由落体同样适用
[例1]从距地面125米的高处,每隔相同的时间由静止释放一个小球队,不计空气阻力,g=10米/秒2,当第11个小球刚刚释放时,第1个小球恰好落地,试求:
(1)相邻的两个小球开始下落的时间间隔为多大?
(2)当第1个小球恰好落地时,第3个小球与第5个小球相距多远?
(拓展)将小球改为长为5米的棒的自由落体,棒在下落过程中不能当质点来处理,但可选棒上某点来研究。
[例2]一条铁链AB长为0.49m,悬于A 端,使其自然下垂,然后让它自由下落,求整个铁链通过悬点下方2.45m处的小孔o时需要的时间是多少?
应着眼于整段,⊿t=t2-t1=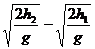 7.5×10-2s(h1=h2-l=2.45-0.49)。
7.5×10-2s(h1=h2-l=2.45-0.49)。
[例3]某人在室内以窗户为背景摄影时,恰好把窗外从高处落下的一个石子摄在照片中,已知本次摄影的爆光时间是0.02s,量得照片中石子运动痕迹的长度为1.6cm,实际长度为100cm的窗框在照片中的长度为4.0cm,凭以上数据,你知道这个石子闯入镜头时大约已经运动了多长时间?(g取10m/s2)
爆光的0.2s内石子下落了S=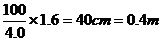 ,在该段时间的中点时刻瞬时速度为
,在该段时间的中点时刻瞬时速度为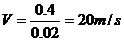 ,此速度为石子闯入镜头0.01s时的速度,此时石子已经运动的时间为t
,此速度为石子闯入镜头0.01s时的速度,此时石子已经运动的时间为t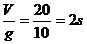 ,实际已经运动的时间为2-0.01=2s。
,实际已经运动的时间为2-0.01=2s。
4.初速为零的匀变速直线运动
①前1s、前2s、前3s……内的位移之比为1∶4∶9∶……
②第1s、第2s、第3s……内的位移之比为1∶3∶5∶……
③前1m、前2m、前3m……所用的时间之比为1∶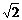 ∶
∶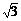 ∶……
∶……
④第1m、第2m、第3m……所用的时间之比为1∶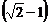 ∶(
∶(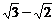 )∶……
)∶……
解析典型问题之2 :注意匀变速直线运动中各个公式的区别和联系,灵活选用公式解题
推论公式是“枝叶”,一个特征: ,物理意义是做匀变速直线运动的物体在相邻相等时间间隔内位移差相等;二个中点公式:时间中点
,物理意义是做匀变速直线运动的物体在相邻相等时间间隔内位移差相等;二个中点公式:时间中点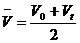 ,位移中点
,位移中点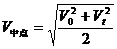 ;三个等时比 例 式:对于初速度为零的匀加速直线运动有,S1:S2:S3……=1:4:9……,SⅠ:SⅡ:SⅢ……=1:3:5……,V1:V2:V3……=1:2:3……;两个等位移比[例]式:对于初速度为零的匀加速直线运动有,
;三个等时比 例 式:对于初速度为零的匀加速直线运动有,S1:S2:S3……=1:4:9……,SⅠ:SⅡ:SⅢ……=1:3:5……,V1:V2:V3……=1:2:3……;两个等位移比[例]式:对于初速度为零的匀加速直线运动有,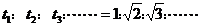 和
和
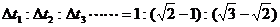
[例6]一列车共20节车箱,它从车站匀加速开出时,前5节车厢经过站在车头旁边的人的时间为t秒,那么:
(1)第三个5节车厢经过人的时间为多少?
(2)若每节车厢长为L,则车尾经过人时的速度多大?
(3)车正中点经过人时速度为多大?
(4)车经过人身旁总时间为多少?
[例7]水平导轨AB的两端各有一竖直的挡板A和B,AB=4米,物体自A开始以4m/s的速度沿导轨向B运动,已知物体在碰到A或B以后,均以与挡板碰前大小相等的速度反弹回来,并且物体在导轨上作匀减速运动的加速度大小相同,为了使物体最终能停在AB的中点,则这个加速度的大小应为多少?-4/(2n+1)
解析典型问题之3:注意汽车刹车中的“刹车陷阱”
[例8]
一汽车在平直的公路上以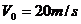 做匀速直线运动,刹车后,汽车以大小为
做匀速直线运动,刹车后,汽车以大小为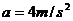 的加速度做匀减速直线运动,那么刹车后经8s汽车通过的位移有多大?50m
的加速度做匀减速直线运动,那么刹车后经8s汽车通过的位移有多大?50m
分析与解:首先必须弄清汽车刹车后究竟能运动多长时间。选V0的方向为正方向,则根据公式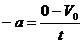 ,可得
,可得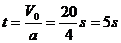
这表明,汽车并非在8s内都在运动,实际运动5s后即停止。所以,将5s代入位移公式,计算汽车在8s内通过的位移。即
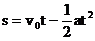
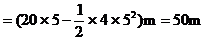
不少学生盲目套用物理公式,“潜在假设”汽车在8s内一直运动,根据匀减速直线运动的位移公式可得:
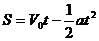

这是常见的一种错误解法,同学们在运用物理公式时必须明确每一个公式中的各物理量的确切含义,深入分析物体的运动过程。
解析典型问题之4:注意对由公式求得“结果”的正确取舍。
[例9]汽车以20m/s的速度做匀速运动,某时刻关闭发动机而做匀减速运动,加速度大小为5m/s2,则它关闭发动机后通过t=37.5m所需的时间为( A )
A.3s; B.4s C.5s D.6s
错解:设汽车初速度的方向为正方向,即V0=20m/s,a=-5m/s2,s=37.5m.
则由位移公式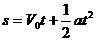 得:
得: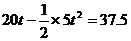
解得:t1=3s,t2=5s.即A、C二选项正确。
分析纠错:因为汽车经过t0=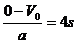 已经停止运动,4s后位移公式已不适用,故t2=5s应舍去。即正确答案为A。
已经停止运动,4s后位移公式已不适用,故t2=5s应舍去。即正确答案为A。
练习1.为了测定某辆轿车在平直路上起动时的加速度(轿车起动时的运动可近似看做匀加速运动),某人拍摄了一张在同一底片上多次爆光的照片(如下图),如果拍摄时每隔2s爆光一次,
轿车车身总长为4.5m,那么这辆轿车的加速度约为:(B)
A、1m/s2 B、2m/s2 C、3m/s2 D、4m/s2
 注意:车身的长度对应的实际长度(每个刻度即为0.5m),再用⊿s=aT2求解,⊿s=20.1m-12m,T=2s,所以a=2m/s2。
注意:车身的长度对应的实际长度(每个刻度即为0.5m),再用⊿s=aT2求解,⊿s=20.1m-12m,T=2s,所以a=2m/s2。
练习2。两木块自左向右运动,现用高速摄象机在同一底片上多次爆光,记录下每次爆光时木块的位置,如图所示,连续两次爆光的时间间隔是相等的,由图可知:(c)
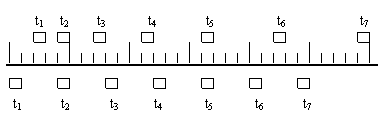 A、在时刻t2以及时刻t3两木块速度相等
A、在时刻t2以及时刻t3两木块速度相等
B、在时刻t3两木块速度相等
C、在时刻t3和时刻t4之间某瞬时两木块速度相等
D、在时刻t4和时刻t5之间某瞬时两木块速度相等
讲评:匀速运动的速度V=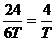 (T为两次爆光的时间间隔),而另一个物体有⊿S=恒量,所以为匀加速直线运动,由图数据:⊿S=1=
(T为两次爆光的时间间隔),而另一个物体有⊿S=恒量,所以为匀加速直线运动,由图数据:⊿S=1=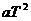 ,所以,V3=
,所以,V3=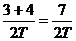 ,V4=
,V4=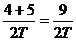 ,选C。
,选C。
第三节 自由落体与竖直上抛运动
目的要求
复习自由落体运动的规律。
知识要点:
3.初速度为零(或末速度为零)的匀变速直线运动
做匀变速直线运动的物体,如果初速度为零,或者末速度为零,那么公式都可简化为:
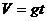 ,
,
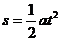 ,
, 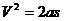 ,
, 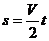
以上各式都是单项式,因此可以方便地找到各物理量间的比[例]关系。
2.匀变速直线运动中几个常用的结论
①Δs=aT 2,即任意相邻相等时间内的位移之差相等。可以推广到sm-sn=(m-n)aT 2
②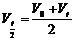 ,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
,某段时间的中间时刻的即时速度等于该段时间内的平均速度。
 ,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
,某段位移的中间位置的即时速度公式(不等于该段位移内的平均速度)。
可以证明,无论匀加速还是匀减速,都有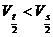 。
。
[例4]物体沿一直线运动,在t时间内通过的路程为S,它在中间位置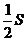 处的速度为V1,在中间时刻
处的速度为V1,在中间时刻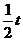 时的速度为V2,则V1和V2的关系为( ABC )
时的速度为V2,则V1和V2的关系为( ABC )
A.当物体作匀加速直线运动时,V1>V2; B.当物体作匀减速直线运动时,V1>V2;
C.当物体作匀速直线运动时,V1=V2; D.当物体作匀减速直线运动时,V1<V2。
[例5]一个质量为m的物块由静止开始沿斜面下滑,拍摄此下滑过程得到的同步闪光(即第一次闪光时物块恰好开始下滑)照片如图1所示.已知闪光频率为每秒10次,根据照片测得物块相邻两位置之间的距离分别为AB=2.40cm,BC=7.30cm,CD=12.20cm,DE=17.10cm.由此可知,物块经过D点时的速度大小为_______m/s;滑块运动的加速度为_____.(保留3位有效数字)
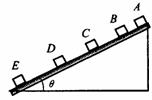 分析与解:据题意每秒闪光10次,所以每两次间的时间间隔T=0.1s,根据中间时刻的速度公式得
分析与解:据题意每秒闪光10次,所以每两次间的时间间隔T=0.1s,根据中间时刻的速度公式得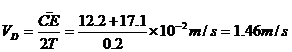 .
.
根据 得
得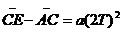 ,所以
,所以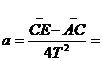 2.40m/s2.
2.40m/s2.
1、匀变速直线运动是在相等的时间里速度的变化量相等的直线运动。基本规律有:
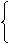 υt=υ0+at
υt=υ0+at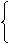
|
 s=υ0t+ at2/2
s=υ0t+ at2/2
s=υ平t
利用上面式子时要注意:
⑴、以上五个公式中共有五个物理量:s、t、a、V0、Vt,除时间t外,s、V0、Vt、a均为矢量。一般以V0的方向为正方向,以t=0时刻的位移为零,这时s、Vt和a的正负就都有了确定的物理意义。
(2) 这五个物理量中只有三个是独立的,可以任意选定。只要其中三个物理量确定之后,另外两个就唯一确定了。每个公式中只有其中的四个物理量,当已知某三个而要求另一个时,往往选定一个公式就可以了。如果两个匀变速直线运动有三个物理量对应相等,那么另外的两个物理量也一定对应相等。
[例1]关于加速度与速度、位移的关系,以下说法正确的是:(D)
A、υ0为正,a为负,则速度一定在减小,位移也一定在减小;
B、υ0为正,a为正,则速度一定在增加,位移不一定在增加;
C、υ0与a同向,但a逐渐减小,速度可能也在减小;
D、υ0与a反向,但a逐渐增大,则速度减小得越来越快(在停止运动前)
[例2]一物体由静止开始做匀加速直线运动,加速度大小为a1,经时间t后做匀减速直线运动,加速度大小为a2,若再经时间t恰能回到出发点,则a1:a2应为:(C)
A、1:1 B、1:2 C、1:3 D、1:4
解析:强化整体的匀变速来处理:S1=a1t2/2,而S2=-S1,此过程去了还返回且整段是匀变速,所以有:S=V1t-a2t2/2,V1= a1t 即可得。注意规律均为矢量式,约定以V0为正方向,减速运动尽量取整段。
解析典型问题之1:注意位移、速度和加速度的矢量性。
[例3]竖直向上抛出一物体,已知其出手时的速度是5m/s,经过3s,该物体落到抛出点下某处,速度为25m/s,已知该物体在运动过程中加速度不变,求该加速度的大小及方向。
错解:由题意知V0=5m/s,Vt=25m/s,所以加速度a=(Vt-V0)/t=6.67m/s2.
分析纠错:由于速度是矢量,处理同一直线上的矢量运算,必须先选定正方向,将矢量运算转化为代数运算。
取向上为正方向,由题意知:V0=5m/s,Vt=-25m/s,所以加速度a=(Vt-V0)/t=-10m/s2.
加速度为负,表示加速度的方向与正方向相反,即a的方向竖直向下。
5. 加速度:描述物体速度变化快慢的物理量,a=△υ/△t (又叫速度的变化率)是矢量。a的方向只与△υ的方向相同(即与合外力方向相同)

 a方向 υ方向相同时 作加速运动;
a方向 υ方向相同时 作加速运动;
 a方向 υ方向相反时 作减速运动;
a方向 υ方向相反时 作减速运动;
加速度的增大或减小只表示速度变化快慢程度增大或减小,不表示速度增大或减小。
思考:(1)a=0但V≠0 (匀速直线运动)
a≠0但V=0 (竖直上抛至最高点)
即a、V无关,而a是反映V变化之快慢
(2)a变化表示何意?a变化则V必变化吗?
(3)a=-3m/s2是什么含义?如何判定加速还是减速?
解析典型问题之 3.注意弄清速度、速度的变化和加速度的区别和联系。
加速度是描述速度变化的快慢和方向的物理量,是速度的变化和所用时间的比值,加速度a的定义式是矢量式。加速度的大小和方向与速度的大小和方向没有必然的联系。只要速度在变化,无论速度多小,都有加速度;只要速度不变化,无论速度多大,加速度总是零;只要速度变化快,无论速度是大、是小或是零,物体的加速度就大。
加速度的与速度的变化ΔV也无直接关系。物体有了加速度,经过一段时间速度有一定的变化,因此速度的变化ΔV是一个过程量,加速度大,速度的变化ΔV不一定大;反过来,ΔV大,加速度也不一定大。
[例4]下列描述的运动中,可能存在的是( )
A.速度变化很大,加速度很小 B.速度变化方向为正,加速度方向为负
C.速度变化越来越快,加速度越来越小 D.速度越来越大,加速度越来越小
[例5]关于速度和加速度的关系,下列说法中正确的是( )
A.速度变化得越多,加速度就越大
B.速度变化得越快,加速度就越大
C.加速度大小保持不变,速度方向也保持不变
D.加速度大小不断变小,速度大小也不断变小
[例6]一物体作匀变速直线运动,某时刻速度的大小为4m/s,1s后速度的大小变为10m/s.在这1s内该物体的( AD ).
A 位移的大小可能小于4m B 位移的大小可能大于10m
C 加速度的大小可能小于4m/s2 D 加速度的大小可能大于10m/s2.
第二节 匀变速直线运动规律及应用
目的要求:
熟练掌握匀变速运动的规律,并能灵活运用其规律解决实际问题。
知识要点:
4. 速度--描述运动快慢的物理量,是位移对时间的变化率。
平均速度:在变速直线运动中,运动物体的位移和所用时间的比值,υ=s/t(方向为位移的方向)
瞬时速度:对应于某一时刻(或某一位置)的速度,方向为物体的运动方向。
速率:即时速度的大小即为速率;
平均速率:为质点运动的路程与时间之比,它的大小与相应的平均速度之值可能不相同*
解析典型问题之 2.注意弄清瞬时速度和平均速度的区别和联系。
瞬时速度是运动物体在某一时刻或某一位置的速度,而平均速度是指运动物体在某一段时间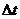 或某段位移
或某段位移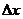 的平均速度,它们都是矢量。当
的平均速度,它们都是矢量。当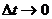 时,平均速度的极限,就是该时刻的瞬时速度。
时,平均速度的极限,就是该时刻的瞬时速度。
[例3]甲、乙两辆汽车沿平直公路从某地同时驶向同一目标,甲车在前一半时间内以速度V1做匀速直线运动,后一半时间内以速度V2做匀速直线运动;乙车在前一半路程中以速度V1做匀速直线运动,后一半路程中以速度V2做匀速直线运动,则( A )。
A.甲先到达; B.乙先到达; C.甲、乙同时到达; D.不能确定。
分析与解:设甲、乙车从某地到目的地距离为S,则对甲车有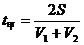 ;对于乙车有
;对于乙车有
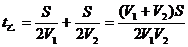 ,所以
,所以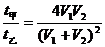 ,由数学知识知
,由数学知识知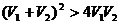 ,故t甲<t乙,即正确答案为A。
,故t甲<t乙,即正确答案为A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com