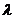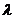1线段的定比分点定义：设P₁,P₂是直线L上的两点，点P是L上不同于P₁,P₂的任意一点，则存在一个实数，使，叫做点P分有向线段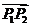所成的比当点P在线段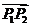上时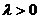，；当点P在线段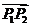或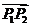的延长线上时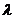，<0

2定比分点的向量表达式：点P分有向线段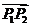所成的比是，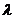

则(O为平面内任意点)

3定比分点的坐标公式: 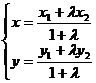,其中P₁(x₁,y₁), P₂(x₂,y₂), P (x,y)

4中点坐标公式: 当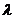=1时，分点P为线段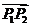的中点，即有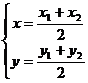

5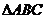的重心坐标公式：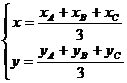

6图形平移的定义:设F是坐标平面内的一个图形，将图上的所有点按照同一方向移动同样长度，得到图形F^’，我们把这一过程叫做图形的平移

7平移公式: 设点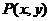按向量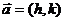平移后得到点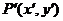，则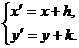(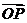＝+);这个公式叫做点的平移公式.

曲线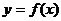按向量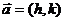平移后所得的曲线的函数解析式为：y′-k=f(x′-h), 一般再换成y=f(x-h)+k

2.熟练运用掌握平移公式

1.掌握线段的定比分点和中点坐标公式

8.利用超声波遇到物体发生反射，可测定物体运动的有关量.图甲中仪器A 和B通过电缆线相接，B为超声波反射与接收一体化装置，而仪器A为B提供超声波信号源而且能将B收到的超声波信号进行处理并在屏幕上显示其波形.现固定装置B，并将它对准匀速行驶的小车C，使其每隔固定时间T₀发射一短促的超声波脉冲(如图乙中幅度大的波形)，而B接收到的由小车C反射回的超声波经仪器A处理后显示如图乙中幅度较小的波形，反射滞后的时间已在乙图中标出，其中T₀和△T为已知量，另外还知道该测定条件下声波在空气中的速度为v₀，则根据所给信息，求小车的运动方向和小车速度的大小.

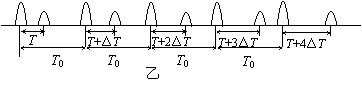
解:从图可以看出接收到反射波的时间越来越长，说明小车远离B，即小车向右运动.

发出第一个脉冲时，设车仪相距s₀，有:

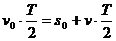　　　　　 ①　　　　　 (3分)

经T₀发出第二个脉冲，车仪相距.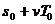

第二个脉冲追上车时:

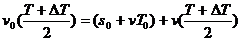　　　　 ②　　　 (3分)

由①②得:　　　　 (2分)

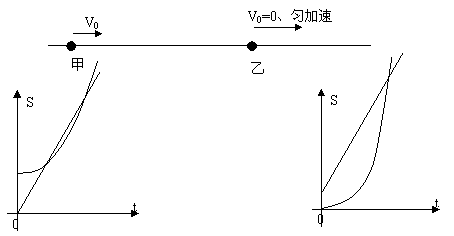
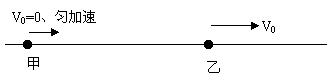
[例]在平直轨道上有相距为S的甲、乙两个物体，它们同时同向开始运动，甲以初速度V_甲、加速度a_甲做匀加速直线运动；乙以初速度为0、加速度为a_乙做匀加速直线运动。设甲能从乙旁边通过而不互相影响，下列情况可能发生的是：(　 CD　 )

A、当a_甲＝a_乙时，甲、乙只能相遇一次。

B、当a_甲＞a_乙时，甲、乙可能相遇二次。

C、当a_甲＞a_乙时，甲、乙可能相遇一次。

D、当a_甲＜a_乙时，甲、乙可能相遇二次。

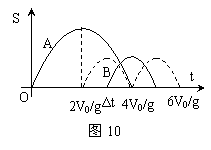
[例] 在地面上以初速度2V₀竖直上抛一物体A后，又以初速V₀同地点竖直上抛另一物体B，若要使两物体能在空中相遇，则两物体抛出的时间间隔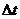必须满足什么条件？(不计空气阻力)

分析与解：如按通常情况，可依据题意用运动学知识列方程求解，这是比较麻烦的。如换换思路，依据s=V₀t-gt²/2作s-t图象，则可使解题过程大大简化。如图10所示，显然，两条图线的相交点表示A、B相遇时刻，纵坐标对应位移S_A=S_B。由图10可直接看出Δt满足关系式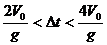时， AB可在空中相遇。

[例]18、摩托车在平直公路上从静止开始起动，a₁=1.6m/s²,稍后匀速运动，然后减速，a₂=6.4m/s²,直到停止，共历时130s，行程1600m.试求：

(1)摩托车行驶的最大速度V_m.

(2)若摩托车从静止起动，a₁、a₂不变，直到停止，行程不变，所需最短时间为多少？

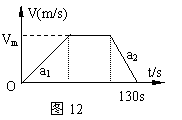分析与解：(1)整个运动过程分三个阶段：匀加速运动；匀速运动；匀减速运动。可借助V-t图表示，如图12所示。利用推论有：

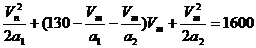
解得：V_m=12.8m/s.(另一根舍去)

(2)首先要回答摩托车以什么样的方式运动可使得时间最短。借助V-t图象可以证明：当摩托车先以a₁匀加速运动，当速度达到V_m^/时，紧接着以a₂匀减速运动直到停止时，行程不变，而时间最短，如图13所示，设最短时间为t_min,

则,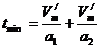　　　　

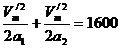
由上述二式解得：V_m^/=64m/s,故t_min=5os,即最短时间为50s.

2、追及和相遇问题的求解方法

分析“追及”、“相遇”问题时，一定要抓住两个关系(时间关系、位移关系)；通过画草图找到两物体的位移关系是解题的突破口。

方法1：利用不等式求解。利用不等式求解，思路有二：其一是先求出在任意时刻t，两物体间的距离y=f(t),若对任何t，均存在y=f(t)>0,则这两个物体永远不能相遇；若存在某个时刻t，使得y=f(t)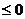,则这两个物体可能相遇。其二是设在t时刻两物体相遇，然后根据几何关系列出关于t的方程f(t)=0,若方程f(t)=0无正实数解，则说明这两物体不可能相遇；若方程f(t)=0存在正实数解，则说明这两个物体可能相遇。

方法2：利用图象法求解。利用图象法求解，其思路是用位移图象求解，分别作出两个物体的位移图象，如果两个物体的位移图象相交，则说明两物体相遇。

3种追击模型：

模型1：(匀速物体追同向初速度为零的匀加速的物体，两着距离有最小值的条件：速度相等)　

[例]Bus由静止开始以1m/s的加速度前进，车后25m处，某人开始以6m/s的速度匀速追车，能否追上？如追不上，求两者的最小距离。

[例]甲、乙两质点，相距S=10m，乙在前、甲在后，沿着同一条直线、向同一个方向、同时开始运动；甲以速度V=8m/s做匀速运动，乙由静止开始以加速度a做匀加速运动，为使两车可相遇一次， a 所满足的关系？

拓展：两车相遇两次或不相遇的条件又是什么呢？

模型2：(初速度为零的匀加速直线运动的物体追赶同向匀速直线运动的物体时，追上之前距离最大的条件：为两者速度相等

[例]甲、乙两质点，相距S=8m，乙在前、甲在后，沿着同一条直线、向同一个方向、同时开始运动；乙做速度为V₀=6m/s的匀速直线运动，甲由静止开始做加速度为a=4m/s²的匀加速直线运动(1)甲用多长时间追上乙？(2)甲追上乙时速度多大？(3)甲追上乙之前何时相距最大？(4)相距的最大距离是多少？

模型3匀减速物体追及同向匀速物体时，恰能追上或恰好追不上的临界条件为：即将靠近时，追及者速度等于被追及者的速度；

[例] 火车以速率V₁向前行驶，司机突然发现在前方同一轨道上距车为S处有另一辆火车，它正沿相同的方向以较小的速率V₂作匀速运动，于是司机立即使车作匀减速运动，加速度大小为a,要使两车不致相撞，求出a应满足关式。

分析与解：设经过t时刻两车相遇，则有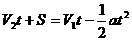，整理得：

要使两车不致相撞，则上述方程无解，即

解得。

[例] 一列快车正以20m/s的速度在平直轨道上运动时，发现前方180m处有一货车正以6m/s速度匀速同向行驶，快车立即制动作匀减速运动，经40s才停止，问是否发生碰车事故？(会发生碰车事故)

设在t时刻两物体相遇，则有：

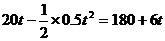，即：。

因为，所以两车相撞。

模型4、匀速物体追同向匀减速的物体，追上前两者具有最大距离的条件：速度相等

[例]甲车在前以15m/s的速度匀速行驶，乙车在后以9m/s的速度行驶。当两车相距32m时，甲车开始刹车，加速度大小为1m/s²。问(1)两车间的最大距离(2)经多少时间乙车可追上甲车？

　 分析：乙此追上甲车可能有两种不同情况：甲车停止前被追及和甲车停止后被追及。究竟是哪一种情况，应根据解答结果，由实际情况判断。

　 解答：设经时间t追上。依题意：

　　　 v_甲t-at²/2+L=v_乙t

　　　 15t-t²/2+32=9t

　　　 t=16s　 t=-4s(舍去)

　　甲车刹车的时间

　　　 t′=v₀/a=15s

　　显然，甲车停止后乙再追上甲。

　　甲车刹车的位移

　　　 s_甲=v₀²/2a=15²/2=112.5m

　　乙车的总位移

　　　 s_乙=s_甲+32=144.5m

　　　 t=s_乙/v_乙=144.5/9=16.06s

[练习](2007全国Ⅰ23题)甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9m/s的速度跑完全程；乙从起跑后到接棒前的运动是匀加速的。为了确定乙起跑的时机，需在接力区前适当的位置设置标记。在某次练习中，甲在接力区前S₀=13.5m处作了标记，并以V=9m/s的速度跑到此标记时向乙发出起跑口令。乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒。已知接力区的长度为L=20m。

求：(1)此次练习中乙在接棒前的加速度a；

(2)在完成交接棒时乙离接力区末端的距离。

[练习](2008宁夏卷17).甲乙两车在公路上沿同一方向做直线运动，它们的v-t图象如图所示。两图象在t=t₁时相交于P点，P在横轴上的投影为Q，△OPQ的面积为S。在t=0时刻，乙车在甲车前面，相距为d。已知此后两车相遇两次，且第一次相遇的时刻为t′，则下面四组t′和d的组合可能是

　A. t′＝t₁ ,d=S　　　　　 B. t′=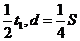

　C. t′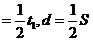　　 D. t′=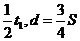

　　 答案：D

[解析]本题考查追击相遇问题。在t₁时刻如果甲车没有追上乙车，以后就不可能追上了，故t′ ＜t₁，A错；从图像中甲、乙与坐标轴围成的面积即对应的位移看，甲在t₁时间内运动的位移比乙的多S，当t′ =0.5 t₁时，甲的面积比乙的面积多出S，即相距d=S，选项D正确。此类问题要抓住图像的交点的物理意义

1、 追及和相遇是指两物体同一时刻到达同一位置。找出两者的时间关系、位移关系是解决追及问题的关键，追和被追的两物体的速度相等(同向运动)是能追上、追不上，两者距离有极值的临界条件

[例1]甲、乙两车同时同地同向出发，在同一水平公路上做直线运动，甲以初速度V₁=16m/s，加速度a₁=4m/s²做匀减速直线运动，乙车以初速度V₂=4m/s，加速度a₂=1m/s²做匀加速直线运动，求；(1)两车再次相遇前两者间的最大距离

(2)两车再次相遇所需的时间　 答案：14．4m　　 4.9s

2、　 速度--时间图象(υ-t图)

(1)　　　 图象的意义：反映运动物体的速度随时间的变化关系。

(2)　　　 必须明确图象中任何一点(交点)、线、截距、斜率，线下面积的含义，

(3)　　　 明确线的形状所代表的具体运动

平行t轴的直线---匀速直线运动

斜线---匀变速直线运动

曲线--- 变加速直线运动

(4)某点的斜率表示该时刻的加速度

解析典型问题1： 位移图象和速度图象的区别和联系　

[例2]AB两物体同时同地沿同一方向运动，如图6所示为A物体沿直线运动时的位置与时间关系图，如图7为B物体沿直线运动的速度时间图试问：(1)AB两物体在0--8秒内的运动情况；(2)AB两物体在8秒内的总位移和总路程分别是多少

解析典型问题2：图象的基本应用

[例3]一个物体竖直向上抛出，如果在上升阶段和下降阶段所 受的空气阻力数值相同，那么在图中:

(1)哪一个能正确反映物体的速度变化(以竖直向上为正方向)？(　　 )

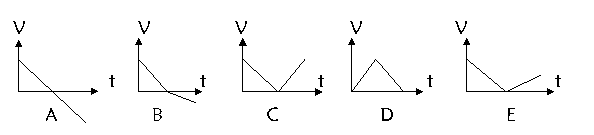(2)哪一个能正确反映物体的速率变化？(　　 )　　　　　　　

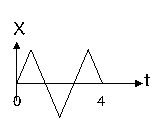[例4]某物体的运动图象如图所示，若图中X表示物体的位移，　　　 则物体(　)

A、做往复运动　　　　　 B、做匀速直线运动　　　　　

C、朝某一方向直线运动　 D、无法确定运动状态

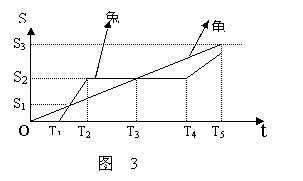[例5]龟兔赛跑的故事流传至今，按照龟兔赛跑的故事情节，兔子和乌龟的位移图象如图3所示，下列关于兔子和乌龟的运动正确的是 (D)

A．兔子和乌龟是同时从同一地点出发的　 　　　　　　　　

B．乌龟一直做匀加速运动，兔子先加速后匀速再加速

C．骄傲的兔子在T₄时刻发现落后奋力追赶，但由于速度比乌龟的速度小，还是让乌龟先到达预定位移S₃

D．在0-T₅时间内，乌龟的平均速度比兔子的平均速度大

　 分析与解：从图3中看出，0-T₁这段时间内，兔子没有运动，而乌龟在做匀速运动，所以A选项错；乌龟一直做匀速运动，兔子先静止后匀速再静止，所以B选项错；在T₄时刻以后，兔子的速度比乌龟的速度大，所以C选项错；在0-T₅时间内，乌龟位移比兔子的位移大，所以乌龟的平均速度比兔子的平均速度大，即D选项正确。

解析典型问题2：利用图象解题

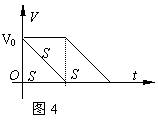[例6] 两辆完全相同的汽车,沿水平直路一前一后匀速行驶,速度均为V₀,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中所行的距离为s,若要保证两辆车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为:(B　 )

(A)s 　　 (B)2s　　 　　　 (C)3s　 　　　 (D)4s

[例7] 两支完全相同的光滑直角弯管(如图7所示)现有两只相同小球a和a^/ 同时从管口由静止滑下，问谁先从下端的出口掉出？(假设通过拐角处时无机械能损失)　　　

分析与解：首先由机械能守恒可以确定拐角处V₁> V₂，而两小球到达出口时的速率V相等。又由题意可知两球经历的总路程s相等。由牛顿第二定律，小球的加速度大小a=gsinα，小球a第一阶段的加速度跟小球a^/第二阶段的加速度大小相同(设为a₁)；小球a第二阶段的加速度跟小球a^/第一阶段的加速度大小相同(设为a₂)，根据图中管的倾斜程度，显然有a₁> a₂。根据这些物理量大小的分析，在同一个V-t图象中两球速度曲线下所围的面积应该相同，且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等，如果同时到达(经历时间为t₁)则必然有s₁>s₂，显然不合理。如图8所示。因此有t₁< t₂，即a球先到。

[例8] 如图8所示中AB是一对平行的金属板，在B板加如图9的方波电压，在0~T/2时间内U_B=U₀>0,现有一电子从A板上的小孔进入两板间的电场区内,设电子的初速、重力影响均可忽略,则(　 AB　 )

A、若电子是在t=0时刻进入的，它将一直向B板运动；

B、若电子是在t=T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上；

C、若电子是在t=3T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上；

D、若电子是在t=T/2时刻进入的，它可能时而向B板运动

练习1、 一个固定在水平面上的光滑物块，其左侧面是斜面AB，右侧面是曲面AC,如图5所示。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑，比较它们到达水平面所用的时间：(　 B )

　 　　A.p小球先到　 　　　　B.q小球先到　　

C.两小球同时到　 　　　　　　　D.无法确定

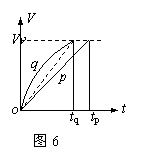分析与解：可以利用V-t图象(这里的V是速率，曲线下的面积表示路程s)定性地进行比较。在同一个V-t图象中做出p、q的速率图线，如图6所示。显然开始时q的加速度较大，斜率较大；由于机械能守恒，末速率相同，即曲线末端在同一水平图线上。为使路程相同(曲线和横轴所围的面积相同)，显然q用的时间较少。

练习2、有两个光滑固定斜面AB和BC，且A和C两点在同一水平面上，斜面BC比斜面AB长(如图)，一个滑块自A点以速度v_A上滑，到达B点时速度减小为零，紧接着沿BC滑下，设滑块从A点到C点的总时间是t_c，那么下列四个图中，正确表示滑块速度的大小v随时间t变化规律的是( 　C 　)

练习3、某人在医院做了一次心电图，结果如图所示。如果心电图仪卷动纸带的速度为1.5 m/min ，图中方格纸每小格长 1 mm ，则此人的心率为(　　 )

A.80次/ min　　　　 B.70次/ min　　　 　C.60次/ min　　　　　 D.50次/ min

练习4、一质点沿直线运动时的速度-时间图线如图16所示，则以下说法中正确的是：( CD )

A．第1s末质点的位移和速度都改变方向。

B．第2s末质点的位移改变方向。

C．第4s末质点的位移为零。

D．第3s末和第5s末质点的位置相同。

错解：选B、C。

分析纠错：速度图线中，速度可以直接从纵坐标轴上读出，其正、负就表示速度方向，位移为速度图线下的“面积”，在坐标轴下方的“面积”为负。

由图16中可直接看出，速度方向发生变化的时刻是第2s末、第4s末，而位移始终为正值，前2s内位移逐渐增大，第3s、第4s内又逐渐减小。第4s末位移为零，以后又如此变化。第3s末与第5s末的位移均为0.5m.故选项CD正确。

所以正确答案是选项C、D。

练习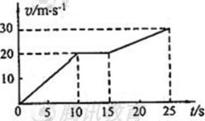5、(2008山东卷17)质量为1500kg 的汽车在平直的公路上运动，v-t图象如图所示。由此可求(ABD)

A．前25s 内汽车的平均速度

B．旦前10s 内汽车的加速度

C．C 前10s 内汽车所受的阻力

D．15-25s内合外力对汽车所做的功

解析：通过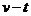图像的面积就是物体的位移，所以能求出面积，还知道时间，所以能求出平均速度，A对。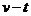图像的斜率就是物体的加速度，所以能得到10秒内的加速度，B对。不知道汽车的牵引力，所以得不出受到的阻力，C错。15到25汽车的初速度和末速度都知道，由动能定理，可以得出合外力做的功，D对

[高考考点]物体运动图像的理解

[易错提醒]有的学生有可能把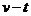看成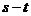，也有可能不能用到动能定理来解题。

练习6(2008海南卷8)t＝0时，甲乙两汽车从相距70 km的两地开始相向行驶，它们的v－t图象如图所示．忽略汽车掉头所需时间．下列对汽车运动状况的描述正确的是

　 　A．在第1小时末，乙车改变运动方向

　 　B．在第2小时末，甲乙两车相距10 km

　 　C．在前4小时内，乙车运动加速度的大小总比甲车的大

　 　D．在第4小时末，甲乙两车相遇

[答案]：BC

[解析]：速度图像在t轴下的均为反方向运动，故2h末乙车改变运动方向，A错；2h末从图像围成的面积可知乙车运动位移为30km，甲车位移为30km，相向运动，此时两车相距70km-30km-30km=10km，B对；从图像的斜率看，斜率大加速度大，故乙车加速度在4h内一直比甲车加速度大，C对；4h末，甲车运动位移120km，乙车运动位移30m，两车原来相距70km，故此时两车还相距20km，D错。

练习7(2008广东卷10)某人骑自行车在平直道路上行进，图中的实线记录了自行车开始一段时间内的v-t图像，某同学为了简化计算，用虚线作近似处理，下列说法正确的是

A．在t₁时刻，虚线反映的加速度比实际的大

B．在0－t₁时间内，由虚线计算出的平均速度比实际的大

C．在t₁-t_-2时间内，由虚线计算出的平均速度比实际的大

D．在t₃-t_-4时间内，虚线反映的是匀速运动

[答案]BD

[解析]v－t图线的斜率表示物体的加速度，v－t图线与坐标轴围成的面积表示物体的位移，据此判断选项B、D正确。需要注意的是若为曲线，则曲线的切线的斜率表示物体的加速度。

第五节　 追及与相遇问题

目的要求

　　 复习追击与相遇问题的计算。

知识要点：

1、　 位移--时间图象(S-t图)

(1)　　　 图象的意义：反映运动的位移随时间的变化关系。

(2)　　　 必须明确图象中任何一点(交点)、线、截距、斜率的含义，

(3)　　　 明确线的形状所代表的具体运动

平行t轴的直线---静止

斜线---匀速直线运动

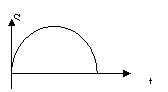抛物线---匀变速直线运动

(4)某点的斜率表示该时刻的瞬时速度

[例1]右上图物体如何运动？下图物体的

V大小、方向如何变化？

23. ( 16 分)

用a 表示跳蚤起跳的加速度，v表示离地时的速度，则对加速过程和离地后上升过程分别有

v²=2ad₂　　 v²=2gh₂

若假想人具有和跳蚤相同的加速度a ，令V表示在这种假想下人离地时的速度，H 表示与此相应的竖直高度，则对加速过程和离地后上升过程分别有

V²=2ad₁　　 V²=2gH

由以上各式可得H=

代人数值，得　 H=63m

　练习1.如图9所示，悬挂的直杆AB长为L₁，在其下L₂处，有一长为L₃的无底圆筒CD，若将悬线剪断，则直杆穿过圆筒所用的时间为多少？

分析与解：直杆穿过圆筒所用的时间是从杆B点落到筒C端开始，到杆的A端落到D端结束。

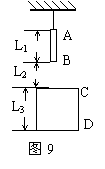设杆B落到C端所用的时间为t₁,杆A端落到D端所用的时间为t₂,由位移公式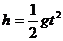得：

，

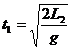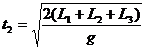
所以，。

练习2(2008上海卷11)某物体以30m/s的初速度竖直上抛，不计空气阻力，g取10m/s²。5s内物体的(AB)

(A)路程为65m

(B)位移大小为25m，方向向上

(C)速度改变量的大小为10m/s

(D)平均速度大小为13m/s，方向向上

[解析]：初速度30m/s，只需要3s即可上升到最高点，位移为h₁=30²/20m=45m，再自由落体2s时间，下降高度为h₂=0.5×10×2²m=20m，故路程为65m，A对；此时离地面高25m，位移方向竖直向上，B对；此时速度为v=10×2m/s=20m/s，速度该变量为50m/s，C错；平均速度为25m/5s=5m/s，

第四节 直线运动的图象

目的要求：

明确s-t，v-t图象的物理意义

知识要点：

2.竖直上抛运动的特征量：(1)上升最大高度：S_m=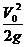.(2)上升最大高度和从最大高度点下落到抛出点两过程所经历的时间：.

[例5]在距地面25米处竖直上抛一球，第1秒末及第3秒末先后经过抛出点上方15米处，试求：

(1)上抛的初速度，距地面的最大高度和第3秒末的速度；

(2)从抛出到落地所需的时间(g=10m/s²)

[例6]一跳水运动员从离水面10 m高的平台上向上跃起，举双臂直体离开台面，此时其重心位于从手到脚全长的中心，跃起后重心升高0．45 m达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)。从离开跳台到手触水面，他可用于完成空中动作的时间是　　　s。(计算时，可以把运动员看作全部质量集中在重心的一个质点。g取10 m /s²，结果保留二位数字)

分析与解：设运动员跃起时的初速度为V₀，且设向上为正，则由V²₀=2gh得：

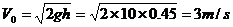
由题意而知：运动员在全过程中可认为是做竖直上抛运动，且位移大小为10m，方向向下，故S=－10m.

由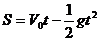得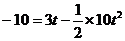：,解得t=1.7s.

[例7](05年高考题全国Ⅰ23题)原地起跳时，先屈腿下蹲，然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速)，加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升，在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据：人原地上跳的“加速距离”d₁=0.50m , “竖直高度”h₁=1.0m；跳蚤原地上跳的“加速距离”d₂=0.00080m , “竖直高度”h₂=0.10m 。假想人具有与跳蚤相等的起跳加速度，而“加速距离”仍为0.50m ，则人上跳的“竖直高度”是多少？