
3.已知平面上直线l的方向向量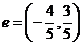 ,点O(0,0)和A(1,-2)在l上的射影分别是
,点O(0,0)和A(1,-2)在l上的射影分别是 ,其中λ等于
( )
,其中λ等于
( )
A、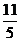 B、
B、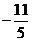 C、2 D、-2
C、2 D、-2
2.已知向量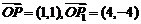 ,且点
,且点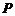 分有向线段
分有向线段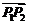 的比为-2,则
的比为-2,则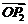 的坐标可以是 ( )
的坐标可以是 ( )
A.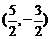 B.
B. 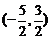 C.
C. 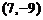 D.
D. 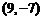
1有向线段的定比分点公式.--注意区分起点与终点,内分与外分,λ是正还是负。求定比分点坐标,还可利用平面几何的方法求出比值|λ|,再确定λ的符号。
2平移公式:要注意新旧标,正确选用公式。
3直角坐标系中通过坐标平移,曲线方程的次数不变.曲线的形状大小不变,变化的只是曲线和坐标点的相互位置关系与曲线方程的形式.给我们的研究曲线带来方便
同步练习 5.4 线段的定比分点 平移
[选择题]
1.已知 的两个顶点
的两个顶点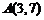 和
和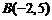 ,若
,若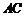 的中点在
的中点在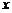 轴上,
轴上, 的中点在
的中点在 轴上,则顶点
轴上,则顶点 的坐标是
(
)
的坐标是
(
)
A.(2,-7) B.(-7,2) C.(-3,-5) D.(5,-3)
 [例1]已知点
[例1]已知点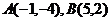 ,线段
,线段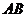 上的三等分点依次为
上的三等分点依次为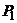 、
、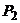 ,求
,求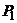 、
、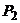 ,点的坐标以及
,点的坐标以及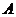 、
、 分
分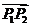 所成的比
所成的比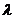
解:设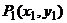 、
、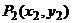 ,
,
则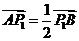 ,
,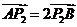
∴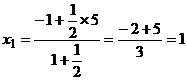
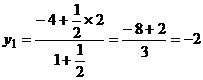 ,即
,即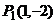
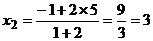 ,
,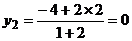 ,即
,即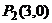
由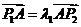 ,得:
,得: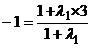 ,∴
,∴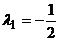 ;
;
由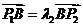 ,得:
,得: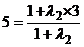 ,∴
,∴ ;
;
点评:定比是根据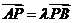 求得的,必须搞清起点、分点、终点
求得的,必须搞清起点、分点、终点 顺序不可搞错
顺序不可搞错
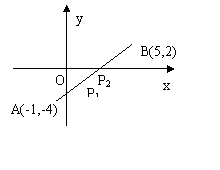
[例2]如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
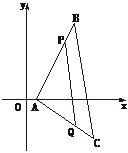
解:设P分 的比为λ1,则
的比为λ1,则
4=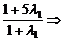 λ1=3,
λ1=3,
即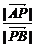 =3,
=3,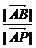 =
=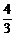 .
.
又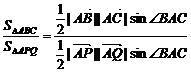
=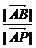 ·
·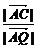 =
=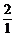 ,
,
∴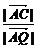 =
=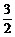 ,即
,即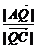 =2.
=2.
设λ2=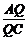 ,则λ2=2.∴xQ=
,则λ2=2.∴xQ=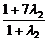 =5,
=5,
yQ=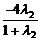 =-
=-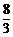 .∴Q(5,-
.∴Q(5,-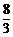 ).
).
[例3]定点A(3,0)为圆x2+y2=1外一点,P为圆上的动点,∠POA的平分线交PA于Q 求Q点的轨迹方程.
求Q点的轨迹方程.
分析:角平分线条件的转化,是本题的关键 设Q(x,y),P(x1,y1),思路是找出P和Q两点坐标之间的关系,列参数方程.
设Q(x,y),P(x1,y1),思路是找出P和Q两点坐标之间的关系,列参数方程.
解:设Q(x,y),P(x1,y1),
点Q分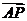 的比为AQ/QP=|OA|/|OP|=3,
的比为AQ/QP=|OA|/|OP|=3,
∴x=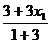 , y=
, y=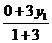 Þx1=4x/3─1, y1=4y/3,
Þx1=4x/3─1, y1=4y/3,
代入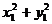 =1化简得: (x─3/4)2+y2=9/16.
=1化简得: (x─3/4)2+y2=9/16.
解法点评:本题巧妙运用了定比分点的概念,并和角平分线性质定理结合起来,要认真体会并在解题中根据条件灵活运用定比分点的概念
[例4]是否存在这样的平移,使抛物线: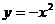 平移后过原点,且平移后的抛物线的顶点和它与
平移后过原点,且平移后的抛物线的顶点和它与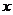 轴的两个交点构成的三角形面积为
轴的两个交点构成的三角形面积为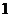 ,若不存在,说明理由;若存在,求出函数的解析式
,若不存在,说明理由;若存在,求出函数的解析式
解:假设存在这样的平移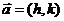 ,
,
由平移公式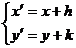
 即
即
代入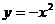 得
得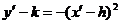 ,
,
即平称后的抛物线为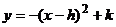 ,顶点为
,顶点为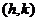
由已知它过原点得: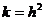 ①
①
令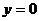 ,求得
,求得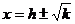
 因此它在
因此它在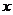 轴上截得的弦长为
轴上截得的弦长为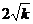
据题意: ,∴
,∴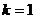 代入①得
代入①得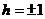
故存在这样的平移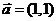 或
或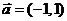
当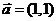 时,平移后解析式为
时,平移后解析式为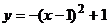 ;
;
当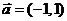 时,平移后解析式
时,平移后解析式
点评:确定平移向量一般是配方法和待定系数法,此题采用待定系数法
[研讨欣赏](2004. 福建)设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, 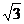 sin2x),x∈R.(Ⅰ)若f(x)=1-
sin2x),x∈R.(Ⅰ)若f(x)=1-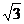 且x∈[-
且x∈[-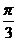 ,
,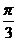 ],求x;
],求x;
(Ⅱ)若函数y=2sin2x的图象按向量c=(m,n)(|m|<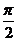 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
解:(Ⅰ)依题设,f(x)=2cos2x+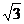 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+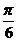 ).
).
由1+2sin(2x+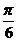 )=1-
)=1-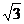 ,得sin(2 x +
,得sin(2 x +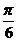 )=-
)=-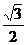 .
.
∵-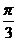 ≤x≤
≤x≤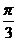 ,∴-
,∴-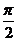 ≤2x+
≤2x+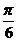 ≤
≤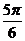 ,
,
∴2x+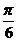 =-
=-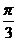 ,即x=-
,即x=-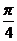 .
.
(Ⅱ)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(Ⅰ)得 f(x)=2sin2(x+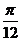 )+1.
)+1.
∵|m|<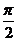 ,∴m=-
,∴m=-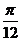 ,n=1.
,n=1.
6.已知点P分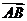 的比为λ(λ≠0),则点P分
的比为λ(λ≠0),则点P分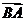 的比为
,点B分
的比为
,点B分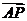 的比为
的比为
答案:1-4.CABA; 5.2或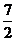 ; 6. (1/λ),(─λ─1)
; 6. (1/λ),(─λ─1)
5.已知点A(x,2),B(5,1),C(-4,2x)在同一条直线上,那么x=
4.将直线l沿y轴负向平移a(a>0)个单位,再沿x轴正向平移a+1个单位,若此时所得的直线与直线l重合,则直线l的斜率是 ( )
A、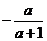 B、
B、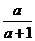 C、
C、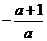 D、
D、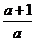
3.按向量 把
把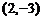 平移到
平移到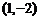 ,则按向量
,则按向量 把点
把点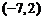 平移到点 ( )
平移到点 ( )
A. (-6,1) B.(-8,3) C.(-6,3) D.(-8,1)
2.△ABC的两个顶点A(3,7)和B(-2,5),若AC的中点在x轴上,BC的中点在y轴上,则顶点C的坐标是 ( )
A (2,-7) ?B (-7,2) C (-3,-5) ?D (-5,-3)
1.已知两点P1(-1,-6)、P2(3,0),点P(-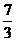 ,y)分有向线段
,y)分有向线段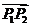 所成的比为λ,则λ、y的值为
( )
所成的比为λ,则λ、y的值为
( )
A -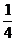 ,8 ?B
,8 ?B 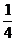 ,-8 ?C -
,-8 ?C -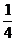 ,-8 ? D 4,
,-8 ? D 4,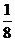
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com