
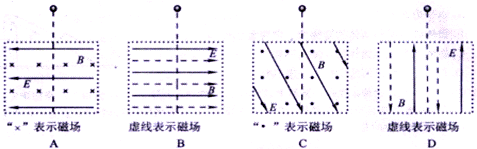
1、如图所示,虚线框中存在匀强电场E和匀强磁场B,它们相互正交或平行.有一个带负电的小球从该复合场上方的某一高度处自由落下,那么,带电小球可能沿直线通过下列的哪些复合场区域 ( )

12.(1)把点A(3,5)按向量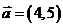 平移,求平移后对应点A’的坐标
平移,求平移后对应点A’的坐标
(2)把函数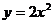 的图象按向量
的图象按向量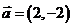 平移得F’,求F’的函数解析式
平移得F’,求F’的函数解析式
解:(1)设A’(x,y),根据平移坐标公式得,得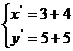 得A’(7,10)
得A’(7,10)
(2)设P (x,y)为F上的任意一点,它在F’上的对应点P’(x’,y’),
则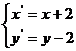 ,即
,即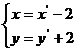
代入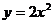 中,得到
中,得到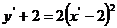
即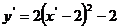
所以F’的函数解析式为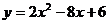
点评:正确选择平移公式,强化代入转移的思想
11.已知点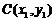 分有向线段
分有向线段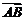 所成的比为
所成的比为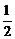 ,点
,点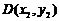 分有向线段
分有向线段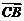 所成的比为
所成的比为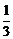 ,
,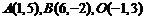 ,试求
,试求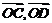 的坐标.
的坐标.
答: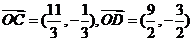
10. 已知ΔABC的三个顶点的坐标是A(x1,y1),B(x2,y2),C(x3,y3),求ΔABC的内心I坐标
解:根据角平分线的性质定理结合定比分点的概念解法相当简洁
设∠A的平分线交BC于点D,
则λ=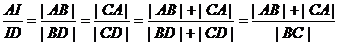
由两点间的距离公式可求出c=|AB|=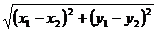 ,
,
类似的可求出|CA|(设为b)和|BC|(设为a),
∴由定比分点的坐标公式可得I(x,y)为: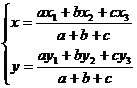
9.已知ΔABC的三个顶点为A(1,5),B(─2,4),C(─6,─4),BC边上有一点M,使ΔABM的面积等于ΔABC面积的1/4.求线段AM的长度
分析:关键是求出点M的坐标,而ΔABC和ΔABC共用∠B和边AB.把两个三角形的面积比转化为它们相对应的边的比,再转化为M分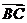 的比λ,这是解决此问题的关键
的比λ,这是解决此问题的关键
解:由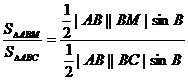 =
=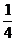 ,知
,知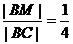 ,
,
而M是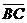 的内分点,故λ=
的内分点,故λ=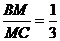 ,
,
由公式求得M(─3,2) ∴|AM|=5
∴|AM|=5
8.已知M为△ABC边AB上的一点,且S△AMC=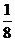 S△ABC,则M分
S△ABC,则M分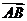 所成的比为
所成的比为
◆练习简答:1-4.AADB; 5. 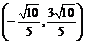 ; 6.10; 7.(8,-4); 8.
; 6.10; 7.(8,-4); 8.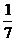 ;
;
[解答题]
7.△ABC的顶点A(2,3),B(-4,-2)和重心G(2,-1),则C点坐标为
6.已知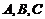 三点共线,
三点共线,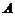 分
分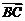 的比为
的比为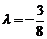 ,
,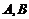 的纵坐标分别为2,5,则点
的纵坐标分别为2,5,则点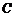 的纵坐标为____________.
的纵坐标为____________.
5.(2005天津)在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),若点C在∠AOB的平分线上且|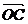 |=2,则
|=2,则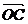 =__________
=__________
4. (2005全国I)点O是三角形ABC所在平面内的一点,满足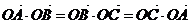 ,则点O是
,则点O是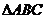 的
( )
的
( )
A. 三个内角的角平分线的交点 B .三条边的垂直平分线的交点
C.三条中线的交点 D. 三条高的交点
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com