
3、 等差数列 中,
中,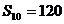 ,那么
,那么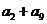 的值是
的值是
(A) 12 (B) 24 (C) 16 (D) 48
2. 若数列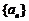 的前n项和为Sn=3n+a,若数列
的前n项和为Sn=3n+a,若数列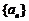 为等比数列,则实数a的取值是
为等比数列,则实数a的取值是
A、3 B、 1 C、 0 D、-1
1. 在公比为整数的等比数列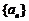 中,如果
中,如果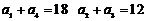 ,则这个等比数列前8项的和为
,则这个等比数列前8项的和为
A.513
B.512
C.510
D.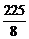
203.实系数一元二次方程的解
实系数一元二次方程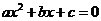 ,
,
①若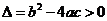 ,则
,则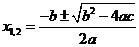 ;
;
②若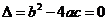 ,则
,则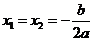 ;
;
③若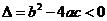 ,它在实数集
,它在实数集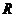 内没有实数根;在复数集
内没有实数根;在复数集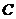 内有且仅有两个共轭复数根
内有且仅有两个共轭复数根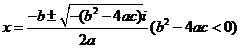 .
.
148.柱体、锥体的体积
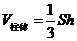 (
(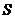 是柱体的底面积、
是柱体的底面积、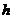 是柱体的高).
是柱体的高).
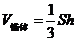 (
(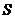 是锥体的底面积、
是锥体的底面积、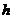 是锥体的高).
是锥体的高).
排列组合
l 分类计数原理(加法原理)
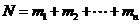 .
.
l 分步计数原理(乘法原理)
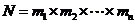 .
.
l 排列数公式
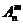 =
= =
=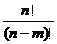 .(
.(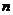 ,
,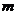 ∈N*,且
∈N*,且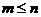 ).
).
注:规定 .
.
l 排列恒等式
(1)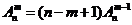 ;
;
(2)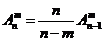 ;
;
(3)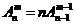 ;
;
(4)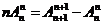 ;
;
(5)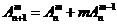 .
.
(6) 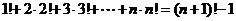 .
.
l 组合数公式
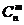 =
=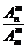 =
=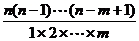 =
=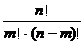 (
(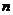 ∈N*,
∈N*,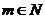 ,且
,且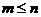 ).
).
l 组合数的两个性质
(1)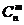 =
=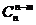 ;
;
(2) 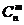 +
+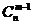 =
=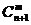 .
.
注:规定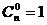 .
.
l 组合恒等式
(1)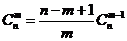 ;
;
(2)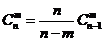 ;
;
(3)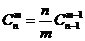 ;
;
(4)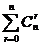 =
=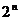 ;
;
(5)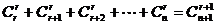 .
.
(6)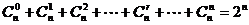 .
.
(7)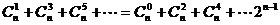 .
.
(8)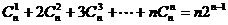 .
.
(9) .
.
(10)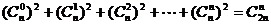 .
.
l 排列数与组合数的关系
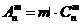 .
.
l 单条件排列
以下各条的大前提是从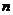 个元素中取
个元素中取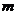 个元素的排列.
个元素的排列.
(1)“在位”与“不在位”
①某(特)元必在某位有 种;②某(特)元不在某位有
种;②某(特)元不在某位有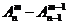 (补集思想)
(补集思想)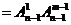 (着眼位置)
(着眼位置) (着眼元素)种.
(着眼元素)种.
(2)紧贴与插空(即相邻与不相邻)
①定位紧贴: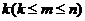 个元在固定位的排列有
个元在固定位的排列有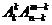 种.
种.
②浮动紧贴: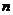 个元素的全排列把k个元排在一起的排法有
个元素的全排列把k个元排在一起的排法有 种.注:此类问题常用捆绑法;
种.注:此类问题常用捆绑法;
③插空:两组元素分别有k、h个( ),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有
),把它们合在一起来作全排列,k个的一组互不能挨近的所有排列数有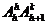 种.
种.
(3)两组元素各相同的插空
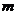 个大球
个大球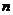 个小球排成一列,小球必分开,问有多少种排法?
个小球排成一列,小球必分开,问有多少种排法?
当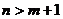 时,无解;当
时,无解;当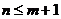 时,有
时,有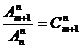 种排法.
种排法.
(4)两组相同元素的排列:两组元素有m个和n个,各组元素分别相同的排列数为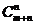 .
.
l 分配问题
(1)(平均分组有归属问题)将相异的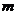 、
、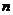 个物件等分给
个物件等分给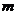 个人,各得
个人,各得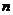 件,其分配方法数共有
件,其分配方法数共有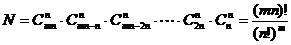 .
.
(2)(平均分组无归属问题)将相异的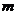 ·
·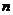 个物体等分为无记号或无顺序的
个物体等分为无记号或无顺序的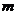 堆,其分配方法数共有
堆,其分配方法数共有
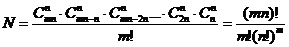 .
.
(3)(非平均分组有归属问题)将相异的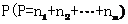 个物体分给
个物体分给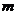 个人,物件必须被分完,分别得到
个人,物件必须被分完,分别得到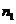 ,
,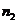 ,…,
,…,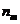 件,且
件,且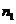 ,
,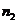 ,…,
,…,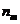 这
这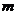 个数彼此不相等,则其分配方法数共有
个数彼此不相等,则其分配方法数共有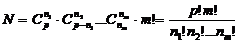 .
.
(4)(非完全平均分组有归属问题)将相异的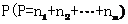 个物体分给
个物体分给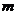 个人,物件必须被分完,分别得到
个人,物件必须被分完,分别得到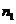 ,
,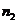 ,…,
,…,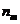 件,且
件,且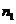 ,
,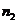 ,…,
,…,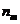 这
这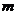 个数中分别有a、b、c、…个相等,则其分配方法数有
个数中分别有a、b、c、…个相等,则其分配方法数有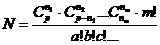
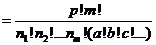 .
.
(5)(非平均分组无归属问题)将相异的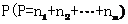 个物体分为任意的
个物体分为任意的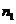 ,
,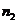 ,…,
,…,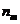 件无记号的
件无记号的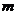 堆,且
堆,且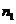 ,
,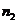 ,…,
,…,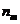 这
这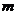 个数彼此不相等,则其分配方法数有
个数彼此不相等,则其分配方法数有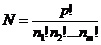 .
.
(6)(非完全平均分组无归属问题)将相异的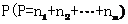 个物体分为任意的
个物体分为任意的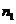 ,
,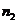 ,…,
,…,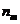 件无记号的
件无记号的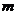 堆,且
堆,且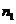 ,
,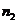 ,…,
,…,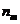 这
这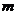 个数中分别有a、b、c、…个相等,则其分配方法数有
个数中分别有a、b、c、…个相等,则其分配方法数有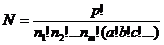 .
.
(7)(限定分组有归属问题)将相异的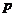 (
(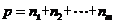 )个物体分给甲、乙、丙,……等
)个物体分给甲、乙、丙,……等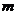 个人,物体必须被分完,如果指定甲得
个人,物体必须被分完,如果指定甲得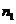 件,乙得
件,乙得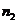 件,丙得
件,丙得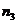 件,…时,则无论
件,…时,则无论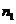 ,
,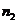 ,…,
,…,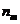 等
等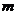 个数是否全相异或不全相异其分配方法数恒有
个数是否全相异或不全相异其分配方法数恒有
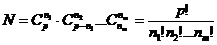 .
.
l “错位问题”及其推广
贝努利装错笺问题:信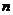 封信与
封信与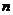 个信封全部错位的组合数为
个信封全部错位的组合数为
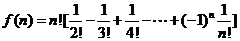 .
.
推广: 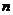 个元素与
个元素与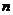 个位置,其中至少有
个位置,其中至少有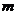 个元素错位的不同组合总数为
个元素错位的不同组合总数为
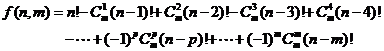
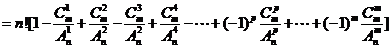 .
.
l
不定方程 的解的个数
的解的个数
(1)方程 (
(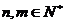 )的正整数解有
)的正整数解有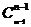 个.
个.
(2) 方程 (
(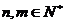 )的非负整数解有
)的非负整数解有 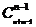 个.
个.
(3) 方程 (
(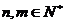 )满足条件
)满足条件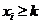 (
(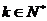 ,
,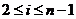 )的非负整数解有
)的非负整数解有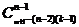 个.
个.
(4) 方程 (
(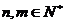 )满足条件
)满足条件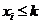 (
(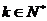 ,
,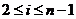 )的正整数解有
)的正整数解有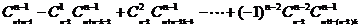 个.
个.
l
二项式定理  ;
;
二项展开式的通项公式
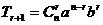
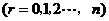 .
.
概率
l 等可能性事件的概率
 .
.
l 互斥事件A,B分别发生的概率的和
P(A+B)=P(A)+P(B).
l
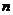 个互斥事件分别发生的概率的和
个互斥事件分别发生的概率的和
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
l 独立事件A,B同时发生的概率
P(A·B)= P(A)·P(B).
l .n个独立事件同时发生的概率
P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An).
l n次独立重复试验中某事件恰好发生k次的概率
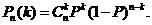 \
\
期望与方差
l .离散型随机变量的分布列的两个性质
(1)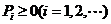 ;
;
(2)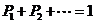 .
.
l 数学期望
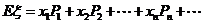
l 数学期望的性质
(1) .
.
(2)若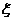 -
-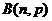 ,则
,则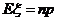 .
.
(3) 若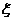 服从几何分布,且
服从几何分布,且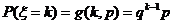 ,则
,则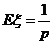 .
.
l 方差
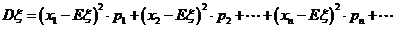
l 标准差
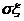 =
=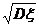 .
.
l 方差的性质
(1)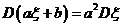 ;
;
(2)若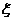 -
-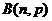 ,则
,则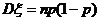 .
.
(3) 若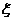 服从几何分布,且
服从几何分布,且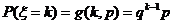 ,则
,则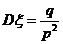 .
.
l 方差与期望的关系
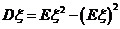 .
.
l 正态分布密度函数
 ,式中的实数μ,
,式中的实数μ,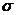 (
(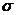 >0)是参数,分别表示个体的平均数与标准差.
>0)是参数,分别表示个体的平均数与标准差.
l .标准正态分布密度函数
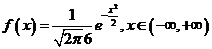 .
.
l
.对于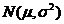 ,取值小于x的概率
,取值小于x的概率
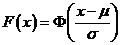 .
.
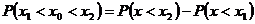
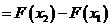
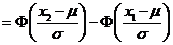 .
.
l 回归直线方程
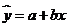 ,其中
,其中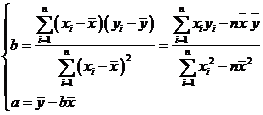 .
.
l 相关系数
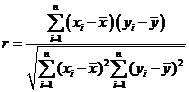
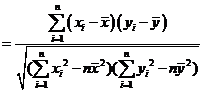 .
.
|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.
极限
l .特殊数列的极限
(1)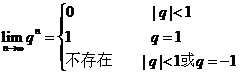 .
.
(2)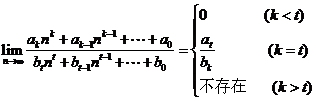 .
.
(3)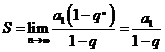 (
(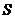 无穷等比数列
无穷等比数列 (
( )的和).
)的和).
l 函数的极限定理
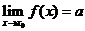
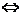
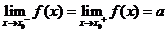 .
.
l .函数的夹逼性定理
如果函数f(x),g(x),h(x)在点x0的附近满足:
(1)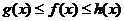 ;
;
(2)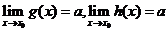 (常数),
(常数),
则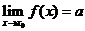 .
.
本定理对于单侧极限和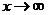 的情况仍然成立.
的情况仍然成立.
l 几个常用极限
(1)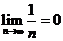 ,
,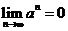 (
(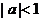 );
);
(2)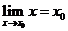 ,
,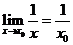 .
.
l 两个重要的极限
(1)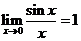 ;
;
(2)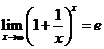 (e=2.718281845…).
(e=2.718281845…).
l .函数极限的四则运算法则
若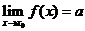 ,
,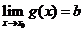 ,则
,则
(1)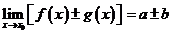 ;
;
(2)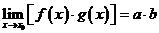 ;
;
(3)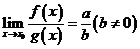 .
.
l .数列极限的四则运算法则
若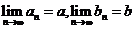 ,则
,则
(1)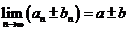 ;
;
(2)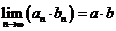 ;
;
(3)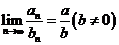
(4)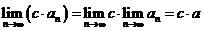 ( c是常数).
( c是常数).
导数
l
.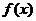 在
在 处的导数(或变化率或微商)
处的导数(或变化率或微商)
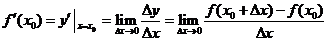 .
.
l 瞬时速度
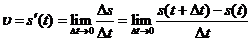 .
.
l 瞬时加速度
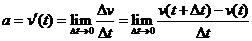 .
.
l .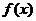 在
在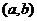 的导数
的导数
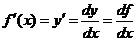
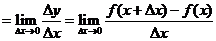 .
.
l
. 函数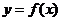 在点
在点 处的导数的几何意义
处的导数的几何意义
函数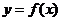 在点
在点 处的导数是曲线
处的导数是曲线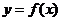 在
在 处的切线的斜率
处的切线的斜率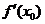 ,相应的切线方程是
,相应的切线方程是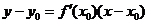 .
.
l .几种常见函数的导数
(1)
 (C为常数).
(C为常数).
(2)
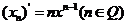 .
.
(3)
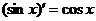 .
.
(4)
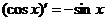 .
.
(5) 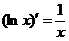 ;
;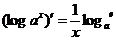 .
.
(6)
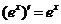 ;
;
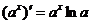 .
.
l .导数的运算法则
(1)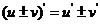 .
.
(2)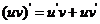 .
.
(3)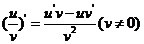 .
.
l .复合函数的求导法则
设函数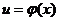 在点
在点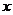 处有导数
处有导数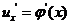 ,函数
,函数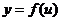 在点
在点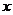 处的对应点U处有导数
处的对应点U处有导数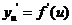 ,则复合函数
,则复合函数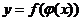 在点
在点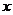 处有导数,且
处有导数,且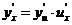 ,或写作
,或写作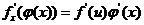 .
.
l
常用的近似计算公式(当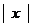 充小时)
充小时)
(1)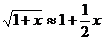 ;
;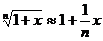 ;
;
(2)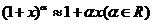 ;
; 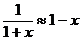 ;
;
(3)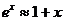 ;
;
(4)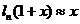 ;
;
(5)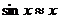 (
(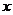 为弧度);
为弧度);
(6)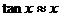 (
(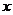 为弧度);
为弧度);
(7)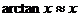 (
(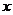 为弧度)
为弧度)
l
.判别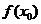 是极大(小)值的方法
是极大(小)值的方法
当函数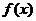 在点
在点 处连续时,
处连续时,
(1)如果在 附近的左侧
附近的左侧 ,右侧
,右侧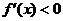 ,则
,则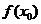 是极大值;
是极大值;
(2)如果在 附近的左侧
附近的左侧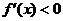 ,右侧
,右侧 ,则
,则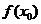 是极小值.
是极小值.
.复数的相等
 .(
.( )
)
l
.复数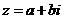 的模(或绝对值)
的模(或绝对值)
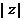 =
=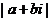 =
=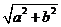 .
.
l .复数的四则运算法则
(1)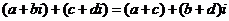 ;
;
(2)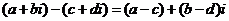 ;
;
(3)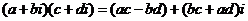 ;
;
(4)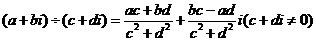 .
.
l .复数的乘法的运算律
对于任何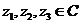 ,有
,有
交换律: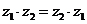 .
.
结合律: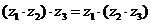 .
.
分配律: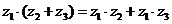 .
.
l .复平面上的两点间的距离公式
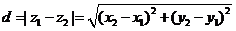 (
(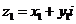 ,
,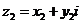 ).
).
l .向量的垂直
非零复数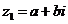 ,
, 对应的向量分别是
对应的向量分别是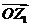 ,
,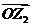 ,则
,则
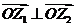
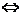
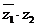 的实部为零
的实部为零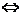
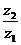 为纯虚数
为纯虚数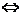
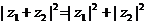
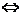
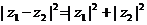
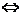
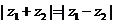
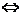
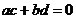
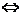
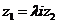 (λ为非零实数).
(λ为非零实数).
147.球的组合体
(1)球与长方体的组合体:
长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:
正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.
(3) 球与正四面体的组合体:
棱长为 的正四面体的内切球的半径为
的正四面体的内切球的半径为 ,外接球的半径为
,外接球的半径为 .
.
146.球的半径是R,则
其体积 ,
,
其表面积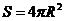 .
.
145.欧拉定理(欧拉公式)
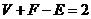 (简单多面体的顶点数V、棱数E和面数F).
(简单多面体的顶点数V、棱数E和面数F).
(1)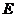 =各面多边形边数和的一半.特别地,若每个面的边数为
=各面多边形边数和的一半.特别地,若每个面的边数为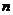 的多边形,则面数F与棱数E的关系:
的多边形,则面数F与棱数E的关系: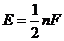 ;
;
(2)若每个顶点引出的棱数为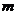 ,则顶点数V与棱数E的关系:
,则顶点数V与棱数E的关系: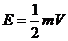 .
.
144.棱锥的平行截面的性质
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比.
143.作截面的依据
三个平面两两相交,有三条交线,则这三条交线交于一点或互相平行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com