
20.设二次函数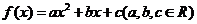 ,已知不论
,已知不论 为何实数恒有
为何实数恒有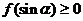
和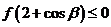 。
。
(Ⅰ)求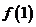 的值;
的值;
(Ⅱ)求证: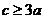 ;
;
(Ⅲ)若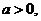 函数
函数 的最大值为8,求
的最大值为8,求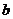 的值。
的值。
19.已知函数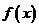 是定义在
是定义在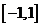 上的奇函数,在
上的奇函数,在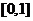 上
上
(Ⅰ)求函数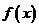 的解析式;并判断
的解析式;并判断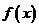 在
在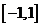 上的单调性(不要求证明)
上的单调性(不要求证明)
(Ⅱ)解不等式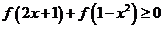 .
.
18.已知 ,
,
(Ⅰ)求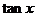 的值;
的值;
(Ⅱ)求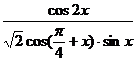 的值.
的值.
17. 已知数列 是等差数列,且
是等差数列,且 ,
,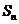 是数列
是数列 的前
的前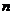 项和.
项和.
(I) 求数列 的通项公式
的通项公式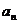 及前
及前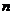 项和
项和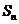 ;
;
(II) 若数列 满足
满足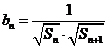 ,且
,且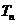 是数列
是数列 的前
的前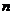 项和,求
项和,求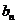 与
与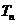 .
.
16.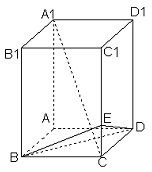 如图所示,在长方体ABCD-A1B1C1D1中,AB = BC = 1,
如图所示,在长方体ABCD-A1B1C1D1中,AB = BC = 1,
BB1 = 2,正是棱CC1上的点,且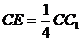
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
15.圆的方程为x2+y2-6x-8y=0,过坐标原点作长为8的弦,求弦所在的直线方程.
14.已知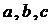 都是正数,且
都是正数,且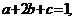 则
则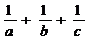 的最小值是
.
的最小值是
.
13.函数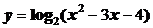 的单调增区间是______________;
的单调增区间是______________;
12. .
.
11.定义在(-∞,+∞)上的偶函数f(x)满足f(x+1)=-f(x), 且f(x)在[-1,0]上是增函数, 下面五个关于f(x)的命题中: ① f(x)是周期函数 ② f(x) 的图象关于x=1对称
③ f(x)在[0,1]上是增函数, ④f(x)在[1,2]上为减函数 ⑤ f(2)=f(0)
正确命题的个数是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com