
4.下列有关细胞结构和功能的叙述,正确的是 ( )
A.在低等植物细胞有丝分裂末期高尔基体参与细胞壁形成
B.在动物细胞有丝分裂间期能观察到纺锤体和中心体
C.分泌蛋白合成后在内质网和细胞质基质中加工
D.质粒和线粒体是既有核酸又有外膜的细胞结构
3.如图是由三个圆所构成的类别关系图,其中Ⅰ为大圆,Ⅱ和Ⅲ分别为大圆之内的小圆。符合这种类别关系的是: ( )
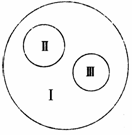 A.Ⅰ-脱氧核糖核酸、Ⅱ-核糖核酸、Ⅲ-核酸
A.Ⅰ-脱氧核糖核酸、Ⅱ-核糖核酸、Ⅲ-核酸
B.Ⅰ-染色体、Ⅱ-DNA、Ⅲ-基因
C.Ⅰ-有机物、Ⅱ-糖类、Ⅲ-蛋白质
D.Ⅰ-蛋白质、Ⅱ-酶、Ⅲ-激素
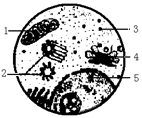
2.右图是电子显微镜视野中观察某细胞的一部分,
下列有关该细胞叙述中,错误的是 ( )
A.结构1和5中含有DNA
B.结构1和3在行使其功能时一定有水生成
C.不含磷脂分子的细胞器是2和3
D.此细胞一定是高等动物具有分泌作用的细胞
1.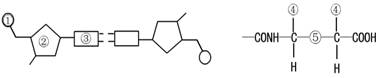 在证明DNA是遗传物质的实验中,赫尔希和蔡斯分别用32P和35S标记噬菌体的DNA和蛋白质,在下图中标记元素所在部位依次是 ( )
在证明DNA是遗传物质的实验中,赫尔希和蔡斯分别用32P和35S标记噬菌体的DNA和蛋白质,在下图中标记元素所在部位依次是 ( )
 A.①、④ B.②、④ C.①、⑤ D.③、⑤
A.①、④ B.②、④ C.①、⑤ D.③、⑤
1 如果|cosθ|=
如果|cosθ|=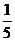 ,
,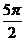 <θ<3π,则sin
<θ<3π,则sin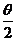 的值等于( )
的值等于( )

2 设5π<θ<6π且cos
设5π<θ<6π且cos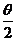 =a,则sin
=a,则sin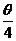 等于( )
等于( )

3 已知tan76°≈4,则tan7°的值约为( )
已知tan76°≈4,则tan7°的值约为( )

4 tan
tan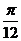 -cot
-cot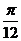 的值等于
的值等于

5 已知sinA+cosA=1,0<A<π,则tan
已知sinA+cosA=1,0<A<π,则tan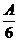 =
= 
6 已知tanα、tanβ是方程7x2-8x+1=0的两根,则tan
已知tanα、tanβ是方程7x2-8x+1=0的两根,则tan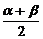 =
= 
7 设25sin2x+sinx-24=0且x是第二象限角,求tan
设25sin2x+sinx-24=0且x是第二象限角,求tan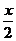

8 已知cos2θ=
已知cos2θ=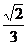 ,求sin4θ+cos4θ的值
,求sin4θ+cos4θ的值
9 求证
求证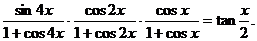
1 已知α、β为锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0
已知α、β为锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0
求证:α+2β=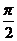
证法1:由已知得3sin2α=cos2β ①
3sin2α=2sin2β ②
①÷②得tanα=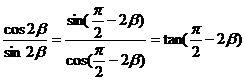
∵α、β为锐角
∴0<β<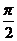 ,0<2β<π,-π<-2β<0,
,0<2β<π,-π<-2β<0,
∴-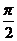 <
<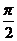 -2β<
-2β<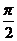
∴α=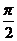 -2β,α+2β=
-2β,α+2β=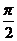
证法2:由已知可得:
3sin2α=cos2β
3sin2α=2sin2β
∴cos(α+2β)=cosα·cos2β-sinα·sin2β
=cosα·3sin2α-sinα·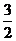 sin2α
sin2α
=3sin2αcosα-sinα·3sinαcosα=0
又由α+2β∈(0,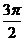 )
)
∴α+2β=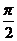
|

∴sin(α+2β)=sinαcos2β+cosαsin2β
=sinα·3sin2α+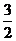 cosα·sin2α
cosα·sin2α
=3sinα(sin2α+cos2α)=3sinα
又由②,得3sinα·cosα=sin2β ③
①2+③2,得9sin4α+9sin2αcos2α=1
∴sinα=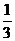 ,即sin(α+2β)=1
,即sin(α+2β)=1
又0<α+2β<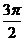
∴α+2β=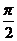
评述:一般地,若所求角在(0,π)上,则一般取此角的余弦较为简便;若所求角在(-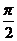 ,
,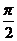 )上,则一般取此角的正弦较为简便;当然,若已知条件与正切函数关系比较密切,也可考虑取此角的正切
)上,则一般取此角的正弦较为简便;当然,若已知条件与正切函数关系比较密切,也可考虑取此角的正切
2 在△ABC中,sinA是cos(B+C)与cos(B-C)的等差中项,
在△ABC中,sinA是cos(B+C)与cos(B-C)的等差中项,
试求(1)tanB+tanC的值 (2)证明tanB=(1+tanC)·cot(45°+C)
(2)证明tanB=(1+tanC)·cot(45°+C)
(1)解:△ABC中,sinA=sin(B+C)
∴2sin(B+C)=cos(B+C)+cos(B-C)
∴2sinBcosC+2cosBsinC=2cosBcosC
∵cosBcosC≠0 ∴tanB+tanC=1
(2)证明:又由上:tanβ=1-tanC=(1+tanC)·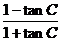
=(1+tanC)·tan(45°-C)=(1+tanC)·cot(45°+C)
3 求值:
求值: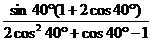
解:原式=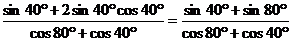

例1已知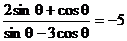 ,求3cos 2q + 4sin 2q 的值
,求3cos 2q + 4sin 2q 的值
解:∵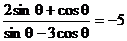 ∴cos q ¹ 0 (否则
2 = - 5 )
∴cos q ¹ 0 (否则
2 = - 5 )
∴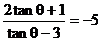 解之得:tan q = 2
解之得:tan q = 2
∴原式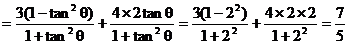
例2已知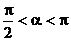 ,
,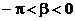 ,tana =
,tana =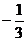 ,tanb =
,tanb =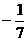 ,求2a + b
,求2a + b
解: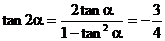 ∴
∴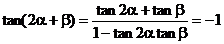
又∵tan2a < 0,tanb < 0 ∴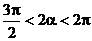 ,
,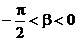
∴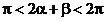 ∴2a + b =
∴2a + b = 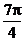
例3已知sina - cosa = 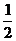 ,
,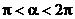 ,求
,求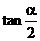 和tana的值
和tana的值
解:∵sina - cosa = 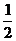 ∴
∴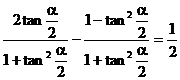
化简得: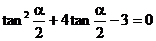
∴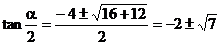
∵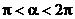 ∴
∴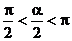 ∴
∴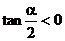
即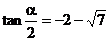
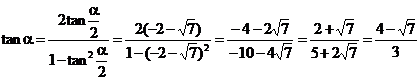
例4已知cosa - cos b = 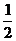 ,sina - sinb =
,sina - sinb = 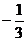 ,求sin(a + b)的值
,求sin(a + b)的值
解:∵cosa - cos b = 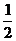 ,∴
,∴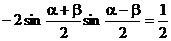 ①
①
sina - sin b =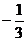 ,∴
,∴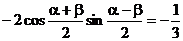 ②
②
∵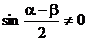 ∴
∴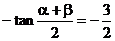 ∴
∴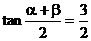
∴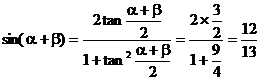
例5求证:sin3asin3a + cos3acos3a = cos32a
证:左边 = (sin3asina)sin2a + (cos3acosa)cos2a
= -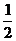 (cos4a - cos2a)sin2a +
(cos4a - cos2a)sin2a + 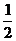 (cos4a + cos2a)cos2a
(cos4a + cos2a)cos2a
= -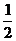 cos4asin2a +
cos4asin2a +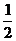 cos2asin2a +
cos2asin2a +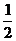 cos4acos2a +
cos4acos2a +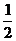 cos2acos2a
cos2acos2a
= 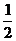 cos4acos2a +
cos4acos2a + 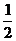 cos2a =
cos2a = 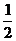 cos2a(cos4a + 1)
cos2a(cos4a + 1)
= 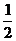 cos2a2cos22a = cos32a = 右边
cos2a2cos22a = cos32a = 右边
∴原式得证
4.万能公式
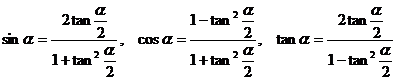
证:1°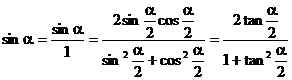
2°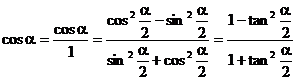
3°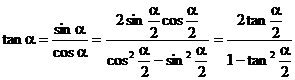
3.半角公式
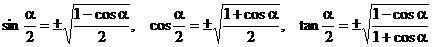
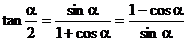
证:1°在  中,以a代2a,
中,以a代2a,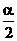 代a 即得:
代a 即得:
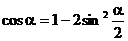 ∴
∴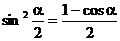
2°在 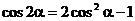 中,以a代2a,
中,以a代2a,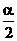 代a 即得:
代a 即得:
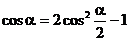 ∴
∴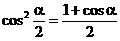
3°以上结果相除得: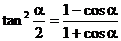
4° 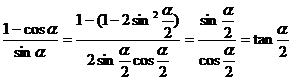
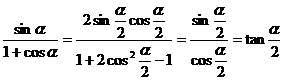
2.和差化积公式的推导
若令a + b = q,a - b = φ,则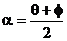 ,
,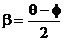 代入得:
代入得:
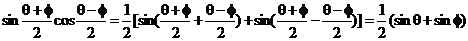
∴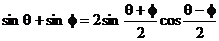
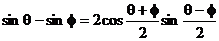
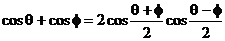
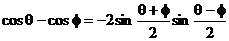
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com