
2.(06上海理,12)三个同学对问题“关于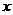 的不等式
的不等式 +25+|
+25+|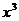 -5
-5 |≥
|≥ 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数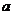 的取值范围”提出各自的解题思路。
的取值范围”提出各自的解题思路。
甲说:“只须不等式左边的最小值不小于右边的最大值”;
乙说:“把不等式变形为左边含变量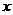 的函数,右边仅含常数,求函数的最值”;
的函数,右边仅含常数,求函数的最值”;
丙说:“把不等式两边看成关于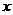 的函数,作出函数图像”;
的函数,作出函数图像”;
参考上述解题思路,你认为他们所讨论的问题的正确结论,即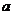 的取值范围是 。
的取值范围是 。
1.已知a>0,b>0,且a+b=1 求证
求证 (a+
(a+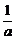 )(b+
)(b+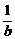 )≥
)≥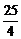 。
。
8.线性规划
(1)平面区域
一般地,二元一次不等式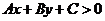 在平面直角坐标系中表示
在平面直角坐标系中表示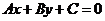 某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式
某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式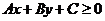 所表示的平面区域时,此区域应包括边界直线,则把直线画成实线。
所表示的平面区域时,此区域应包括边界直线,则把直线画成实线。
说明:由于直线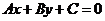 同侧的所有点的坐标
同侧的所有点的坐标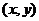 代入
代入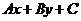 ,得到实数符号都相同,所以只需在直线某一侧取一个特殊点
,得到实数符号都相同,所以只需在直线某一侧取一个特殊点 ,从
,从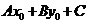 的正负即可判断
的正负即可判断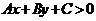 表示直线哪一侧的平面区域。特别地,当
表示直线哪一侧的平面区域。特别地,当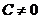 时,通常把原点作为此特殊点。
时,通常把原点作为此特殊点。
 (2)有关概念
(2)有关概念
引例:设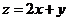 ,式中变量
,式中变量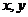 满足条件
满足条件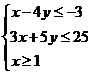 ,求
,求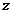 的最大值和最小值。
的最大值和最小值。
由题意,变量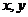 所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域。由图知,原点
所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域。由图知,原点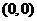 不在公共区域内,当
不在公共区域内,当 时,
时,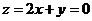 ,即点
,即点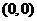 在直线
在直线 :
: 上,作一组平行于
上,作一组平行于 的直线
的直线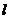 :
: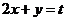 ,
, ,可知:当
,可知:当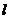 在
在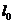 的右上方时,直线
的右上方时,直线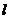 上的点
上的点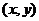 满足
满足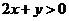 ,即
,即 ,而且,直线
,而且,直线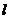 往右平移时,
往右平移时,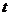 随之增大。
随之增大。
由图象可知,当直线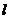 经过点
经过点 时,对应的
时,对应的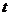 最大,
最大,
当直线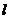 经过点
经过点 时,对应的
时,对应的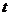 最小,所以,
最小,所以,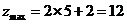 ,
,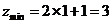 。
。
在上述引例中,不等式组是一组对变量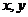 的约束条件,这组约束条件都是关于
的约束条件,这组约束条件都是关于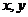 的一次不等式,所以又称为线性约束条件。
的一次不等式,所以又称为线性约束条件。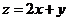 是要求最大值或最小值所涉及的变量
是要求最大值或最小值所涉及的变量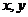 的解析式,叫目标函数。又由于
的解析式,叫目标函数。又由于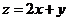 是
是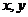 的一次解析式,所以又叫线性目标函数。
的一次解析式,所以又叫线性目标函数。
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题。满足线性约束条件的解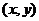 叫做可行解,由所有可行解组成的集合叫做可行域。在上述问题中,可行域就是阴影部分表示的三角形区域。其中可行解
叫做可行解,由所有可行解组成的集合叫做可行域。在上述问题中,可行域就是阴影部分表示的三角形区域。其中可行解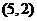 和
和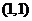 分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解。
分别使目标函数取得最大值和最小值,它们都叫做这个问题的最优解。
课前预习
7.对数不等式
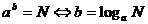
 等,
等,

(1)当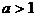 时,
时,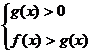 ;
;
(2)当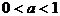 时,
时,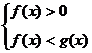 。
。
6.指数不等式
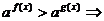
 ;
;
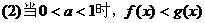 ;
;
5.简单的绝对值不等式
绝对值不等式适用范围较广,向量、复数的模、距离、极限的定义等都涉及到绝对值不等式。高考试题中,对绝对值不等式从多方面考查。
解绝对值不等式的常用方法:
①讨论法:讨论绝对值中的式于大于零还是小于零,然后去掉绝对值符号,转化为一般不等式;
②等价变形:
解绝对值不等式常用以下等价变形:
|x|<a x2<a2
x2<a2 -a<x<a(a>0),
-a<x<a(a>0),
|x|>a x2>a2
x2>a2 x>a或x<-a(a>0)。
x>a或x<-a(a>0)。
一般地有:
|f(x)|<g(x) -g(x)<f(x)<g(x),
-g(x)<f(x)<g(x),
|f(x)|>g(x) f(x)>g (x)或f(x)<g(x)。
f(x)>g (x)或f(x)<g(x)。
4.分式不等式
分式不等式的等价变形: >0
>0 f(x)·g(x)>0,
f(x)·g(x)>0, ≥0
≥0
 。
。
3.一元二次不等式
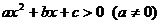 或
或 分
分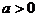 及
及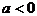 情况分别解之,还要注意
情况分别解之,还要注意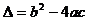 的三种情况,即
的三种情况,即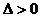 或
或 或
或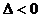 ,最好联系二次函数的图象。
,最好联系二次函数的图象。
2.一元一次不等式
解一元一次不等式(组)及一元二次不等式(组)是解其他各类不等式的基础,必须熟练掌握,灵活应用。
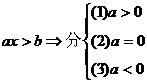 情况分别解之。
情况分别解之。
解不等式是求定义域、值域、参数的取值范围时的重要手段,与“等式变形”并列的“不等式的变形”,是研究数学的基本手段之一。
高考试题中,对解不等式有较高的要求,近两年不等式知识占相当大的比例。
1.不等式同解变形
(1)同解不等式((1)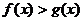 与
与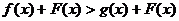 同解;
同解;
(2)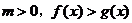 与
与 同解,
同解,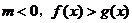 与
与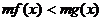 同解;
同解;
(3)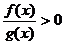 与
与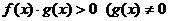 同解);
同解);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com