
16.提示: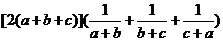

15.提示: 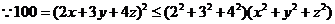

14.提示: 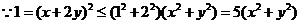
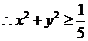 .
.
13.提示: 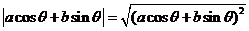
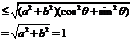
12. 提示:利用不等式解决极值问题,通常设法在不等式一边得到一个常数,并寻找不等式取等号的条件.这个函数的解析式是两部分的和,若能化为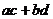 的形式就能利用柯西不等式求其最大值.
的形式就能利用柯西不等式求其最大值.
解:函数的定义域为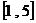 ,且
,且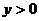 .
.
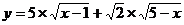

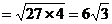
当且仅当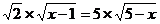 时,等号成立,即
时,等号成立,即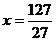 时函数取最大值
时函数取最大值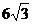 .
.
11. 提示:要证的结论与条件之间的联系不明显,直接由条件推出结论的线索不够清晰.另外,如果从正面证明,需要对某一个分式小于2或两个分式都小于2等进行分类讨论,而从反面证明,则只要证明两个分式都不小于2是不可能的即可.于是考虑采用反证法.
证明:假设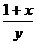 ,
,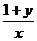 都不小于2,即
都不小于2,即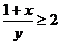 ,且
,且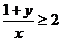 .
.
因为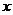 ,
,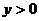 ,所以
,所以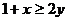 ,且
,且 .把这两个不等式相加,得
.把这两个不等式相加,得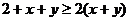 ,
,
从而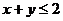 .这与已知条件
.这与已知条件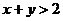 矛盾.因此,
矛盾.因此,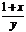 ,
,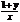 都不小于2是不可能的,即原命题成立.
都不小于2是不可能的,即原命题成立.
10.提示:观察要证明的结论,左边是 个因式的乘积,右边是2的
个因式的乘积,右边是2的 次方,再结合
次方,再结合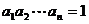 ,发现如果能将左边转化为
,发现如果能将左边转化为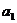 ,
,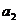 ,…,
,…,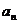 的乘积,问题就能得到解决.
的乘积,问题就能得到解决.
证明:因为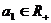 ,所以
,所以 ,即
,即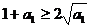 .
.
同理, ,……
,…… .因为
.因为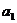 ,
,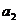 ,…,
,…,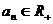 ,由不等式的性质,
,由不等式的性质,
得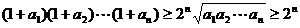 .
.
因为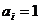 时,
时, 取等号,所以原式在
取等号,所以原式在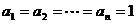 时取等号.
时取等号.
9.分析:观察欲证不等式的特点,左边3项每一项都是两个数的平方之和与另一个数之积,右边是三个数的积的6倍.这种结构特点启发我们采用如下方法.
证明:因为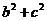 ≥
≥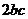 ,
,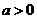 ,所以
,所以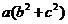 ≥
≥ .
①
.
①
因为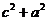 ≥
≥ ,
,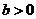 ,所以
,所以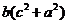 ≥
≥ .
②
.
②
因为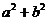 ≥
≥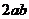 ,
,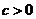 ,所以
,所以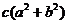 ≥
≥ .
③
.
③
由于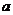 ,
,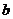 ,
,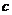 不全相等,所以上述①②③式中至少有一个不取等号,把它们相加得
不全相等,所以上述①②③式中至少有一个不取等号,把它们相加得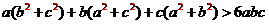 .
.
8.提示: 设切去的正方形边长为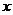 ,无盖方底盒子的容积为
,无盖方底盒子的容积为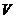 ,则
,则
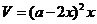
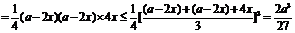
当且仅当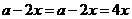 ,即当
,即当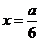 时,不等式取等号,此时
时,不等式取等号,此时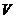 取最大值
取最大值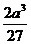 .即当切去的小正方形边长是原来正方形边长的
.即当切去的小正方形边长是原来正方形边长的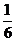 时,盒子容积最大.
时,盒子容积最大.
7.提示: 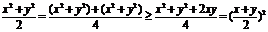 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com