
5.简单的绝对值不等式
①讨论法:讨论绝对值中的式于大于零还是小于零,然后去掉绝对值符号,转化为一般不等式;
②等价变形:
|f(x)|<g(x)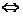 -g(x)<f(x)<g(x),
-g(x)<f(x)<g(x),
|f(x)|>g(x)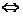 f(x)>g (x)或f(x)<g(x)。
f(x)>g (x)或f(x)<g(x)。
4.分式不等式
分式不等式的等价变形: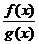 >0
>0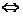 f(x)·g(x)>0,
f(x)·g(x)>0,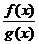 ≥0
≥0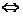
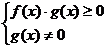 。
。
3.一元二次不等式
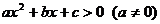 或
或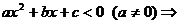 分
分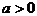 及
及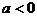 情况分别解之,还要注意
情况分别解之,还要注意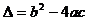 的三种情况,即
的三种情况,即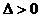 或
或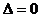 或
或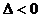 ,最好联系二次函数的图象。
,最好联系二次函数的图象。
2.一元一次不等式
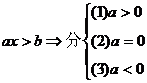 情况分别解之。
情况分别解之。
解不等式是求定义域、值域、参数的取值范围时的重要手段,与“等式变形”并列的“不等式的变形”,是研究数学的基本手段之一。
高考试题中,对解不等式有较高的要求,近两年不等式知识占相当大的比例。
1.不等式同解变形
(1)同解不等式((1)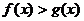 与
与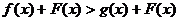 同解;
同解;
(2) 与
与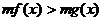 同解,
同解,
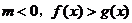 与
与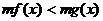 同解;
同解;
(3)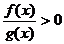 与
与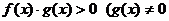 同解);
同解);
3.分析法
证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种方法通常叫做分析法。
2.综合法
利用某些已经证明过的不等式(例如算术平均数与几何平均数的定理)和不等式的性质,推导出所要证明的不等式,这个证明方法叫综合法;
1.比较法
比较法证明不等式的一般步骤:作差-变形-判断-结论;为了判断作差后的符号,有时要把这个差变形为一个常数,或者变形为一个常数与一个或几个平方和的形式,也可变形为几个因式的积的形式,以便判断其正负。
18.证明:(法一)要证原不等式成立,只须证: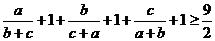
即只须证: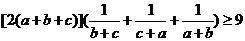
由柯西不等式易知上式显然成立,所以原不等式成立。
(法二)由对称性,不妨设: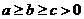 ,则
,则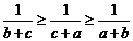 ,
,
所以:(顺序和)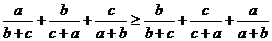 (乱序和)
(乱序和)
(顺序和)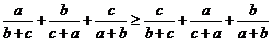 (乱序和)
(乱序和)
将以上两式相加即得: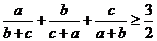 .
.
17. 提示:这是一个与整除有关的命题,它涉及全体正整数,若用数学归纳法证明,第一步应证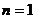 时命题成立;第二步要明确目标,即在假设
时命题成立;第二步要明确目标,即在假设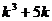 能够被6整除的前提下,证明
能够被6整除的前提下,证明 也能被6整除.
也能被6整除.
证明:1)当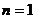 时,
时,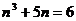 显然能够被6整除,命题成立.
显然能够被6整除,命题成立.
2)假设当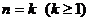 时,命题成立,即
时,命题成立,即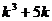 能够被6整除.
能够被6整除.
当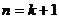 时,
时,
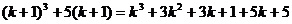
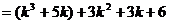
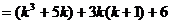 .
.
由假设知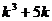 能够被6整除,而
能够被6整除,而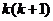 是偶数,故
是偶数,故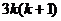 能够被6整除,从而
能够被6整除,从而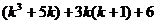 即
即 能够被6整除.因此,当
能够被6整除.因此,当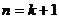 时命题成立.
时命题成立.
由1)2)知,命题对一切正整数成立,即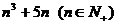 能够被6整除;
能够被6整除;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com