
注意:上述等号“=”成立的条件;
若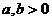 ,则
,则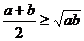 (当且仅当
(当且仅当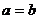 时取等号)
时取等号)
基本变形:①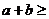 ;
;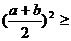 ;
;
②若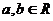 ,则
,则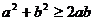 ,
,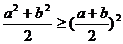
基本应用:①放缩,变形;
②求函数最值:注意:①一正二定三取等;②积定和小,和定积大。
当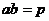 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
当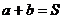 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
常用的方法为:拆、凑、平方;
如:①函数 的最小值
。
的最小值
。
②若正数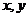 满足
满足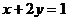 ,则
,则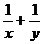 的最小值
。
的最小值
。
(1)一元一次不等式:
Ⅰ、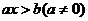 :⑴若
:⑴若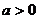 ,则
;⑵若
,则
;⑵若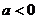 ,则
;
,则
;
Ⅱ、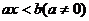 :⑴若
:⑴若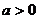 ,则
;⑵若
,则
;⑵若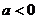 ,则
;
,则
;
(2)一元二次不等式: 一元二次不等式二次项系数小于零的,同解变形为二次项系数大于零;注:要对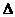 进行讨论:
进行讨论:
(5)绝对值不等式:若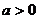 ,则
,则 ;
;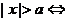 ;
;
注意:(1).几何意义: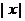 :
;
:
;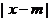 :
;
:
;
(2)解有关绝对值的问题,考虑去绝对值,去绝对值的方法有:
⑴对绝对值内的部分按大于、等于、小于零进行讨论去绝对值;①若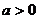 则
则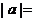 ;②若
;②若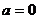 则
则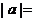 ;③若
;③若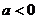 则
则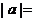 ;
;
(3).通过两边平方去绝对值;需要注意的是不等号两边为非负值。
(4).含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解。
(6)分式不等式的解法:通解变形为整式不等式;
⑴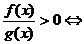 ;⑵
;⑵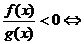 ;
;
⑶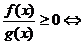 ;⑷
;⑷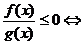 ;
;
(7)不等式组的解法:分别求出不等式组中,每个不等式的解集,然后求其交集,即是这个不等式组的解集,在求交集中,通常把每个不等式的解集画在同一条数轴上,取它们的公共部分。
(8)解含有参数的不等式:
9.不等式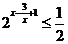 的解集为
.
的解集为
.
8.已知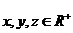 ,
,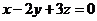 ,则
,则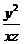 的最小值 .
的最小值 .
7.若不等式|3x-b|<4的解集中的整数有且仅有1,2,3,则b的取值范围 。
6.不等式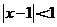 的解集是 .
的解集是 .
5.已知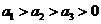 ,则使得
,则使得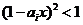
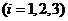 都成立的
都成立的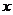 取值范围是
取值范围是
4.已知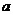 ,b都是实数,那么“
,b都是实数,那么“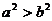 ”是“
”是“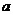 >b”的
条件
>b”的
条件
3. “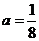 ”是“对任意的正数
”是“对任意的正数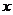 ,
,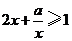 ”的
条件
”的
条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com