
25.(本题10分)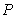 是抛物线
是抛物线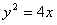 上的一点,过
上的一点,过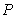 分别作两直线交抛物线于不同的两点A
分别作两直线交抛物线于不同的两点A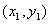 ,B
,B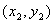 ,
,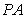 与
与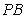 分别交
分别交 轴于
轴于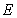 ,
,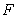 两点.
两点.
(1)若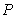 的坐标为(
的坐标为(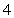 ,
,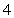 ),直线
),直线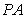 与
与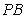 斜率均存在且|
斜率均存在且|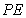 |=|
|=|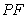 |,求
|,求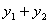 的值;
的值;
(2)若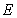 (
(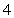 ,
,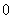 ),是否存在垂直于
),是否存在垂直于 轴的直线
轴的直线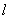 被以
被以 为直径的圆所截得的弦长恒为定值?若存在求出直线
为直径的圆所截得的弦长恒为定值?若存在求出直线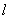 的方程,不存在说明理由.
的方程,不存在说明理由.
台州市2008学年第二学期高二期末质量评估试题
24.(本题8分)设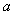 为实数,函数
为实数,函数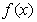 =
=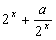 ,
, ∈
∈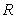 .
.
(1)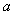 为何值时函数
为何值时函数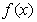 是奇函数?并说明理由;
是奇函数?并说明理由;
(2)当 ∈[
∈[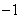 ,
,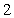 ]时不等式
]时不等式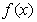
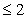 恒成立,求实数
恒成立,求实数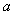 的最大值.
的最大值.
23.(本题8分)已知动圆过定点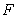 (
(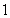 ,
,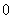 ),且与定直线
),且与定直线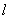 :
: =
=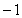 相切.
相切.
(1)求动圆圆心的轨迹 的方程;
的方程;
(2)设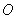 为原点,点
为原点,点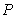 在轨迹
在轨迹 上移动,
上移动,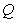 是
是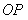 的中点,
的中点,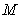 是
是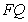 的中点,求点
的中点,求点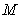
的轨迹方程.
22.(本题8分)设命题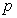 :函数
:函数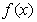 =
=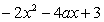 在(
在(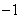 ,+
,+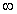 )上单调递减;命题
)上单调递减;命题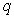 :函数
:函数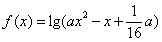 的定义域为
的定义域为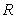 .如果命题
.如果命题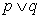 为真,
为真,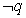 为真,求实数
为真,求实数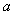 的取值范围.
的取值范围.
21.(本题6分)已知函数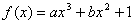 ,当
,当 =
=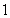 时
时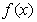 取得极值
取得极值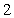
(1)求实数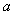 ,
,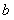 的值;(2)求曲线y=
的值;(2)求曲线y=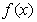 在点(
在点(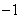 ,
,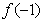 )处的切线方程.
)处的切线方程.
19. . 20. .
17. . 18. .
15. . 16. .
20.已知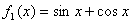 ,记
,记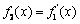 ,
,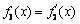 ,…,
,…,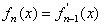
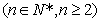 ,则
,则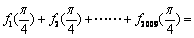 ▲ .
▲ .
台州市2008学年第二学期高二期末质量评估试题
数学答题卷(文科) 2009.07
19.函数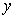 =
=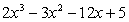 在区间[
在区间[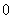 ,
, ]上的最小值是
▲ .
]上的最小值是
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com