
2.
分析:问题分别可通过错位相减的方法及构造二项式定理的方法来解决.转换思维角度,由求导公式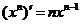 ,可联想到它们是另外一个和式的导数,因此可转化求和,利用导数运算可使问题解法更加简洁明快.
,可联想到它们是另外一个和式的导数,因此可转化求和,利用导数运算可使问题解法更加简洁明快.
解:1.当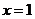 时,
时,
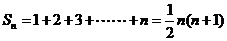
当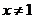 时,
时,
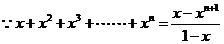 ,
,
两边都是关于x的函数,求导得
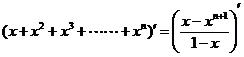 ,
,
即
1.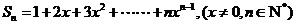
4.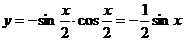 ,
,
∴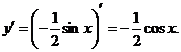
说明:对于函数求导,一般要遵循先化简,再求导的基本原则.求导时,不但要重视求导法则的应用,而且要特别注意求导法则对求导的制约作用.在实施化简时,首先必须注意变换的等价性,避免不必要的运算失误.
根据点和切线确定抛物线的系数
例
已知抛物线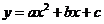 通过点
通过点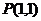 ,且在点
,且在点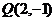 处与直线
处与直线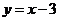 相切,求实数a、b、c的值.
相切,求实数a、b、c的值.
分析:解决问题,关键在于理解题意,转化、沟通条件与结论,将二者统一起来.题中涉及三个未知参数,题设中有三个独立的条件,因此,通过解方程组来确定参数a、b、c的值是可行的途径.
解:∵曲线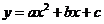 过
过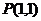 点,
点,
∴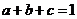 ①
①
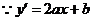 ,∴
,∴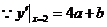
∴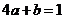 ②
②
又曲线过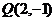 点,∴
点,∴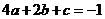 ③.
③.
联立解①、②、③得
说明:利用导数求切线斜率是行之有效的方法,它适用于任何可导函数,解题时要充分运用这一条件,才能使问题迎刃而解.解答本题常见的失误是不注意运用点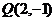 在曲线上这一关键的隐含条件.
在曲线上这一关键的隐含条件.
利用导数求和
例 利用导数求和.
3.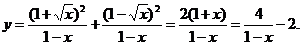
∴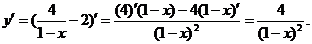
2.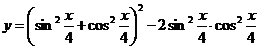
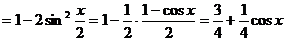
∴
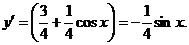
3.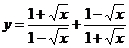 ;4.
;4.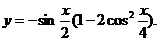
分析:对于比较复杂的函数,如果直接套用求导法则,会使问题求解过程繁琐冗长,且易出错.可先对函数解析式进行合理的恒等变换,转化为易求导的结构形式再求导数.
解:1. ,
,
∴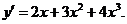
1.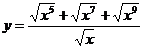 ;2.
;2.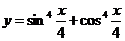 ;
;
4.解法一: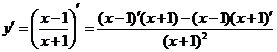
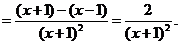
解法二: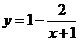 ,
,

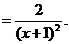
说明:理解和掌握求导法则和公式的结构规律是灵活进行求导运算的前提条件,运算过程出现失误,原因是不能正确理解求导法则,特别是商的求导法同.求导过程中符号判断不清,也是导致错误的因素.从本题可以看出,深刻理解和掌握导数运算法则,再结合给定函数本身的特点,才能准确有效地进行求导运算,才能充分调动思维的积极性,在解决新问题时举一反三,触类旁通,得心应手.
化简函数解析式在求解
例 求下列函数的导数.
3.解法一: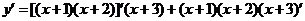
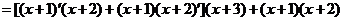
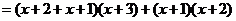
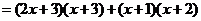
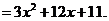
解法二: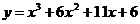 ,
,
∴
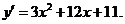
2.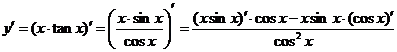
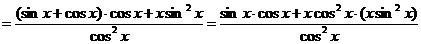
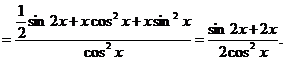
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com