
3.两端取对数,得
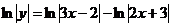 ,
,
两端对x求导,得
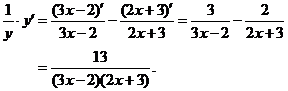
2.注意到 ,两端取对数,得
,两端取对数,得
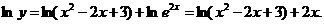
∴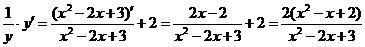
∴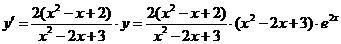
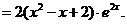
3.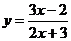 ;4.
;4.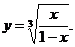
分析:式中所给函数是几个因式积、商、幂、开方的关系.对于这种结构形式的函数,可通过两边取对数后再求导,就可以使问题简单化或使无法求导的问题得以解决.但必须注意取寻数时需要满足的条件是真数为正实数,否则将会出现运算失误.
解:1.取y的绝对值,得 ,两边取寻数,得
,两边取寻数,得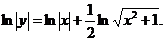
根据导数的运算法则及复合函数的求导法则,两端对x求导,得
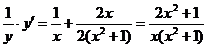 ,
,
∴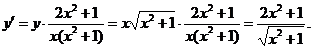
1.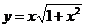 ;2.
;2.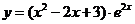 ;
;
4.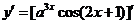
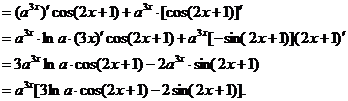
说明:深刻理解,掌握指数函数和对数函数的求导公式的结构规律,是解决问题的关键,解答本题所使用的知识,方法都是最基本的,但解法的构思是灵魂,有了它才能运用知识为解题服务,在求导过程中,学生易犯漏掉符合或混淆系数的错误,使解题走入困境.
解题时,能认真观察函数的结构特征,积极地进行联想化归,才能抓住问题的本质,把解题思路放开.
变形函数解析式求导
例 求下列函数的导数:
(1)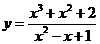 ; (2)
; (2)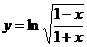 ;
;
(3)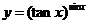 ; (4)
; (4)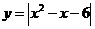 .
.
分析:先将函数适当变形,化为更易于求导的形式,可减少计算量.
解:(1)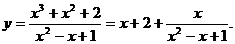
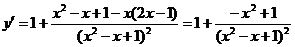 .
.
(2)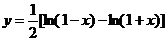 ,
,
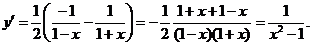
(3)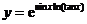
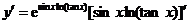
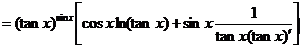


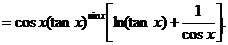
(4)
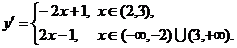
当 时
时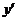 不存在.
不存在.
说明:求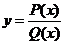 (其中
(其中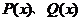 为多项式)的导数时,若
为多项式)的导数时,若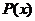 的次数不小于
的次数不小于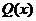 的次数,则由多项式除法可知,存在
的次数,则由多项式除法可知,存在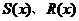 ,使
,使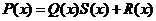 .从而
.从而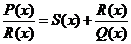 ,这里
,这里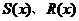 均为多项式,且
均为多项式,且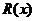 的次数小于
的次数小于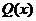 的次数.再求导可减少计算量.
的次数.再求导可减少计算量.
对函数变形要注意定义域.如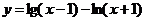 ,则定义域变为
,则定义域变为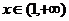 ,所以虽然
,所以虽然 的导数
的导数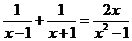 与
与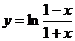 的导数
的导数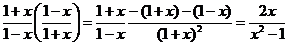 结果相同,但我们还是应避免这种解法.
结果相同,但我们还是应避免这种解法.
函数求导法则的综合运用
例 求下列函数的导数:
3.解法一:设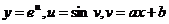 ,则
,则
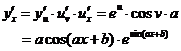
解法二: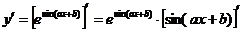
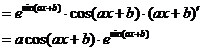
2.解法一:设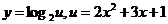 ,则
,则
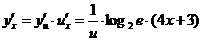
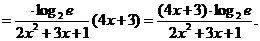
解法二: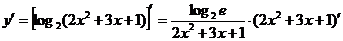
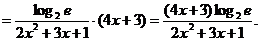
3.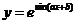 ; 4.
; 4.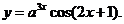
分析:对于比较复杂的函数求导,除了利用指数、对数函数求导公式之外,还需要考虑应用复合函数的求导法则来进行.求导过程中,可以先适当进行变形化简,将对数函数的真数位置转化为有理函数的形式后再求导数.
解:1.解法一:可看成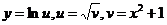 复合而成.
复合而成.
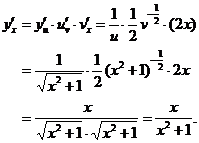
解法二: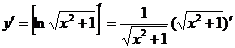

解法三: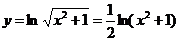 ,
,
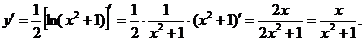
1.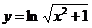 ;2.
;2.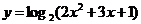 ;
;
3.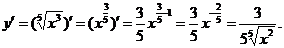
说明:对于简单函数的求导,关键是合理转化函数关系式为可以直接应用公式的基本函数的模式,以免求导过程中出现指数或系数的运算失误.运算的准确是数学能力高低的重要标志,要从思想上提高认识,养成思维严谨,步骤完整的解题习惯,要形成不仅会求,而且求对、求好的解题标准.
根据斜率求对应曲线的切线方程
例 求曲线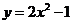 的斜率等于4的切线方程.
的斜率等于4的切线方程.
分析:导数反映了函数在某点处的变化率,它的几何意义就是相应曲线在该点处切线的斜率,由于切线的斜率已知,只要确定切点的坐标,先利用导数求出切点的横坐标,再根据切点在曲线上确定切点的纵坐标,从而可求出切线方程.
解:设切点为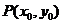 ,则
,则
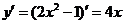 ,∴
,∴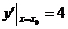 ,即
,即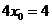 ,∴
,∴
当 时,
时,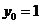 ,故切点P的坐标为(1,1).
,故切点P的坐标为(1,1).
∴所求切线方程为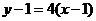
即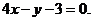
说明:数学问题的解决,要充分考虑题设条件,捕捉隐含的各种因素,确定条件与结论的相应关系,解答这类问题常见的错误是忽略切点既在曲线上也在切线上这一关键条件,或受思维定势的消极影响,先设出切线方程,再利用直线和抛物线相切的条件,使得解题的运算量变大.
求直线方程
例 求过曲线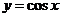 上点
上点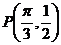 且与过这点的切线垂直的直线方程.
且与过这点的切线垂直的直线方程.
分析:要求与切线垂直的直线方程,关键是确定切线的斜率,从已知条件分析,求切线的斜率是可行的途径,可先通过求导确定曲线在点P处切线的斜率,再根据点斜式求出与切线垂直的直线方程.
解: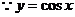 ,∴
,∴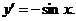
曲线在点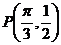 处的切线斜率是
处的切线斜率是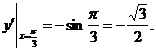
∴过点P且与切线垂直的直线的斜率为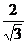 ,
,
∴所求的直线方程为 ,
,
即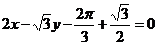 .
.
说明:已知曲线上某点的切线这一条件具有双重含义.在确定与切线垂直的直线方程时,应注意考察函数在切点处的导数 是否为零,当
是否为零,当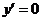 时,切线平行于x轴,过切点P垂直于切线的直线斜率不存在.
时,切线平行于x轴,过切点P垂直于切线的直线斜率不存在.
求曲线方程的交点处切线的夹角
例
设曲线 和曲线
和曲线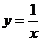 在它们的交点处的两切线的夹角为
在它们的交点处的两切线的夹角为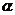 ,求
,求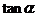 的值.
的值.
分析:要求两切线的夹角,关键是确定在两曲线交点处的切线的斜率.根据导数的几何意义,只需先求出两曲线在交点处的导数,再应用两直线夹角公式求出夹角即可.
解:联立两曲线方程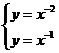 解得两曲线交点为(1,1).
解得两曲线交点为(1,1).
设两曲线在交点处的切线斜率分别为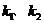 ,则
,则
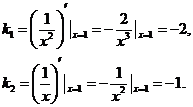
由两直线夹角公式
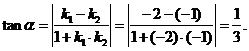
说明:探求正确结论的过程需要灵巧的构思和严谨的推理运算.两曲线交点是一个关键条件,函数在交点处是否要导也是一个不能忽视的问题,而准确理解题设要求则是正确作出结论的前提.
求常函数的导数
例 设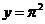 ,则
,则 等于( )
等于( )
A.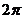 B.
B.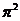 C.0 D.以上都不是
C.0 D.以上都不是
分析:本题是对函数的求导问题,直接利用公式即可
解:因为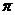 是常数,常数的导数为零,所以选C.
是常数,常数的导数为零,所以选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com